【信息融合】BP神经网络和DS证据理论不确定性信息融合问题【含Matlab源码 2204期】

news2025/2/27 11:27:55

⛄一、 D-S证据理论及解释

证据理论由Dempster在1967年最初提出,并由他的学生Shafer改进推广使之成为符合有限离散领域中推理的形式,因此称为D-S理论。证据理论讨论一个“辨识框架”(Frame of Discernment)Θ,它是关于命题的相互独立的可能答案或假设的一个有限集合。按传统方法可以把Θ的幂集表示为2Θ,它是Θ的所有子集的集合。D-S证据理论对这个辨识框架进行运算,并提供计算幂集元素的逻辑,然后使用这些计算结果完成高和低的不确定性的计算工作。

定义1Θ为鉴别框架,由一完备的互不相容的陈述集合组成,Θ的幂集构成了命题集合。通过传感器信息得到的特征度量作为证据,并通过基本概率赋值函数对所有命题赋予一个可信度,基本概率赋值函数m则是满足下述两个条件的映射:2Θ→[0,1]。

(1)不可能事件基本概率数为0,即m(Φ)=0;
在这里插入图片描述
表示。它表示了既不信任A也不信任A¯¯¯的一种度量,可表示对不知道的度量。

1 证据理论在信息融合中的应用
定义3 假设Bel1和Bel2是相同的框架2Θ上的信任函数,具有基本概率赋值函数m1和m2以及核{A1,A2,…,An}和{B1,B2,…,Bn},并假设
在这里插入图片描述
定义4 假设Bel1,Bel2,…,Beln都是相同框架2Θ上的信任函数,则n个信任函数的组合可写成
(((Bel1⊕Bel2)⊕Bel3)⊕…)⊕Beln
式中⊕表示直和,有组合证据获得的最终证据在组合完成过程中与其次序无关,即满足结合率。

假定两个独立的证据源(传感器信息源)导出的基本概率赋值函数,则利用组合规则可以计算这两个证据共同作用下产生的基本概率赋值函数。

假定两个传感器同时反映对象为A,且
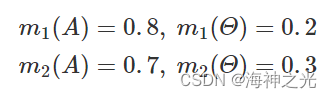
在这里插入图片描述
采用D-S规则进行组合,结果为

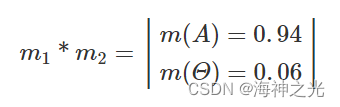
假设一个传感器支持对象A的程度为0.8,而另一个传感器支持的对象是B,程度为0.9,即

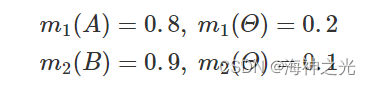
式中,对象A和对象B是相互排斥的描述,经过规则组合并规格化为和1并简化后得到

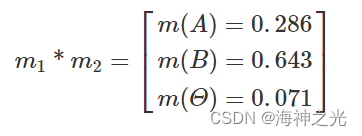
可以看出,信任程度低的对象报告影响了高信任度的对象报告。

当m1(A)=1.0,m2(B)=1.0时,组合公式中的分母为零,D-S规则无法对其进行组合,也就是说,D-S规则无法处理完全不一致的证据。

⛄二、部分源代码

clear all
clc
%data1 m1=[0.5 0.2 0.3];m2=[0 0.45 0.55];m3=[0.45 0.3 0.25];m4=[0.6 0.15 0.25];w=[0.2 0.2 0.3 0.3];
%data2 m1=[0.35 0.5 0.15];m2=[0.15 0.7 0.15];m3=[0.40 0 0.60];m4=[0.2 0.65 0.15];w=[0.25 0.35 0.15 0.25];
%data3
m1=[0.75 0.25 0];m2=[0 0.35 0.65];m3=[0.1 0.3 0.6];m4=[0.1 0.35 0.55];w=[0.1 0.35 0.3 0.25];
%DS
[DS_2,DS_3,DS_4]=DS(m1,m2,m3,m4);
%Yager
[Yager_2,Yager_3,Yager_4]=Yager(m1,m2,m3,m4);
%孙全
[Sunquan_2,Sunquan_3,Sunquan_4]=Sunquan(m1,m2,m3,m4);
%Murphy
[Murphy_2,Murphy_3,Murphy_4]=Murphy(m1,m2,m3,m4);
%邓勇合成公式（加权证据合成法）
[Dengyong_2,Dengyong_3,Dengyong_4]=Dengyong(m1,m2,m3,m4);
%New
[New_2,New_3,New_4]=new(m1,m2,m3,m4,w);