0.参考

贝塞尔(Bezier)曲线与B样条：这个视频讲的很好，尤其是对样条曲线的两种理解方式上，会对后面B样条曲线性质的分析有很大的帮助。本文在前面的部分也会较多的参考这个视频中讲解的内容。但是视频后面讲解B样条曲线的时候稍微简略了一点，因此本文给出我自己的理解。

1.问题起源与插值法的曲线拟合

1.1.问题起源

样条曲线起源于一个常见问题，即已知若干点的条件下，如何得到通过这些点的一条光滑曲线？

一个简答的方法是对曲线进行 插值：在原有数据点上进行填充生成曲线，曲线必经过原有数据点。

1.2.拉格朗日插值

当有多个点的时候，可以使用拉格朗日插值法得到插值的曲线函数表达式：

其中每个函数 $L_k$称为拉格朗日插值基函数。注意这个基的概念，对于后面理解贝塞尔曲线和B样条曲线非常有帮助。

1.3.“基”的概念

我们之前学过的知识中，有很多地方用到了 基 的概念，比如下面的内容：

• 线性代数：向量的线性组合就是在对向量空间的基向量给不同的权重相加，然后得到新的向量。
• 微积分：Taylor展式，Fourier级数：他们都是有基函数，然后最终我们的函数是由很多这种基函数组成的
• Lagrange插值法：一组基的线性组合：前面刚刚提到，我们插值得到的函数其实是由一组基函数组合来的。

1.4.插值存在的Runge现象

插值存在一些问题，比如Runge现象。这是因为插值要求插值函数必须经过所有的插值点，导致非线性程度很严重。

为了解决这个问题，并且考虑到人们往往想要一个比较光滑的曲线，而并不要求曲线通过所有点，所以拟合就产生了。

2.贝塞尔曲线

2.1.控制点的思想

一个简单且行之有效的方法是，把这些点作为限制点，然后在这些限制点中放置一条具有弹性的金属片，最后金属片绕过这些点后的最终状态即为所需曲线。而最终得到的形状曲线，就是样条曲线。这也是该名字的由来，其中金属片就是样条，形成的曲线就是样条曲线。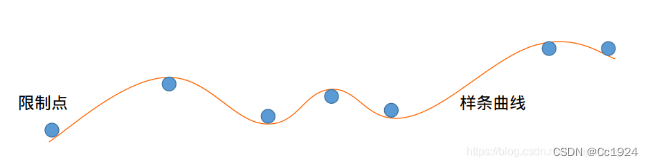
注意：上图中的蓝色圆形可以变的很大，这样生成的样条曲线就离圆心很远了，所以就是明显不通过这些圆心点的。如果把圆的半径缩小成0，那么结果就变成插值了。

2.2.由控制点生成贝塞尔曲线

步骤如下：

1. 先由前2个控制点，按照 $t$ 的比例生成一个中间过程点 $P_i$
   $$P_i=(1-t)P_0+P_1$$
2. 再由后2个控制点，按照 $t$ 的比例生成一个中间过程点 $P_j$
   $$P_j=(1-t)P_1+P_2$$
3. 对两个中间过程点，按照 $t$ 的比例生成最后我们要的曲线上的一个点 $P_x$。
   $$P_x=(1-t)P_i+P_j$$

最后，通过遍历所有的比例值 $t\in [0,1]$，我们就可以得到贝塞尔曲线上的所有点，也就是得到了整条贝塞尔曲线。

如果控制点的个数比3个多呢？那么就要不断重复上面2个点生成1个中间点的过程，直到最后只剩下一个点，这个点就是曲线上的点。所以当有多个控制点的时候，只需要对上面的过程进行多次，最后得到一个曲线上的点$P_x$，然后改变比例$t$，就得到整条贝塞尔曲线了。

2.3.多个控制点时的贝塞尔曲线公式

重要：对贝塞尔曲线公式的两种理解：

1. 从 基 是 基函数 的角度理解：贝塞尔曲线前面的权重$W$就是插值基函数，它是和$t$有关的函数，所以他是有次数的，比如下图所示的就是关于$t$为3次的基函数。后面的点$P$就相当于插值点，也就是给基函数的权重。但是贝塞尔曲线和拉尔朗日插值的不同之处在于，贝塞尔曲线的结果并不全都通过这些插值点。

也就是说，这种理解方式，基 是 基函数，也就是关于$t$的一些函数，而 权重 则是这些 控制点。

这种理解方式就是微积分的理解方式，也就是泰勒展开、级数的理解方式，因为最终我们的曲线是可以用一个函数表示的，而这个函数是由 基函数 施加不同的 权重 得到的，而这个权重就是各个控制点的坐标值。

2. 从 基 是 控制点 的角度理解：

也就是说，这种理解方式，基 是 基向量，也就是控制点；而 权重 则是关于 $t$的一些函数，对于任意一个 $t$确定了之后，我们就可以把函数值算出来，就得到了一个具体的权重值。然后把权重值施加到控制点上，我们就得到了曲线上的一个具体的点。

这种理解方式就是线性代数的理解方式，也就是对向量空间的基向量进行线性组合的理解方式。这里相当于把整个曲线分成一个个的点来看，对于每一个点来说，它对应着一个确定的$t$值，这个确定的$t$值带入函数$W$里面就可以得到确定的权重。然后利用这个确定的权重对控制点进行线性组合，就得到了曲线上的一个点。最后遍历所有的$t$值，我们就得到了曲线上的所有点，也就是得到了整条贝塞尔曲线。

2.4.贝塞尔曲线的递推公式

其实这个很简单，因为前面我们讲解多个控制点的贝塞尔曲线的具体做法时，其实就是按照递推的公式来讲解的它的思路，只不过是写成最终的公式的时候我们可以写出一个最终的结果。而递推公式就是描述了一步步求中间点的过程。

2.5.贝塞尔曲线的性质

• Bezier曲线是BSpline的特例
• 曲线总是通过第一个和最后一个点
• 曲线在始点处的切线落在前两个控制的连线上，曲线在终点处的切线落在最后两个控制点的连线上
• 改变其中任何一个点，整条曲线都会随之改变。这个很容易发现，以为如果从 基 是 基函数 的角度来看就会发现，每个基函数的定义域都是 $t\in [0,1]$。所以一个控制点改变了之后，它会影响整个曲线中这个控制点对应的 基函数 的函数值分量，从而导致整条曲线从头到尾都会受到影响。
• 贝塞尔曲线幂次 = 控制点个数 - 1。 对于一条复杂的曲线，如果使用一个贝塞尔曲线来插值获得目标曲线，就需要通过增加控制点来进行插值，需要的计算也越复杂。幂次的问题很好理解，因为每生成一个中间点幂次就上升一次。
  因此对于复杂曲线，不要求用n-1次曲线，而是让次数低一点，经常使用三次贝塞尔曲线一段一段地拼接成目标曲线，如Ps 或 Ai 中使用钢笔工具画出物体轮廓所做的那样。 如果使用这种方法，确保最终整体曲线一次光滑的条件是在连接点出两侧的斜率相等，即连接点和其两侧控制点共线。

3.B样条曲线

3.1.B样条曲线的基本概念

生成曲线，本质上就是找一组基函数，然后用各个控制点当权重进行线性组合。或者理解为把控制点作为基向量，然后用函数当权重，给定一个$t$带入函数中就得到一个具体的权重值，然后就可以得到曲线上一个点，最后遍历所有的比例$t$就可以得到曲线上的所有点。

下面给出B样条曲线的一些基本概念，然后后面再给出详细的解释。
举例说明如下：

3.2.对B样条的疑问

前面的概念中，不太清楚的就是 控制点(Control Points) 和 节点(Knots) 这两个概念。而且前面的讲解中一开始说了节点的个数和控制点无关，是自己选取的；但是后面又说控制点和节点的个数必须要满足的关系是 $m=n+k+1$，这个属实有点让人疑惑。

另外一个让人不太清楚的就是 次(Degree) 和 阶(Order) 的区别，实际上 阶数 = 次数 + 1。

直接解释这两个问题是无法解释的，因为这个必须从B样条的原理触发，当明白了B样条的原理，自然就可以明白为什么B样条中除了控制点还会有节点，然后才可以推导前面的两个关系式。

3.3.B样条递推公式的过程

我们直接从最终的递推形式的$k$次B样条基函数出发，来解释B样条的思想。所以这里我们把曲线的样条拟合问题变成了对 基函数 的线性组合问题，线性组合的权重变成了各个点的坐标值。

有了控制点，为什么还要使用节点呢？贝塞尔曲线只用控制点就可以了啊？其实这个就是为了改进贝塞尔曲线只有全局特性、没有局部特性的问题，也就是贝塞尔曲线只要修改了一个控制点之后，即使基函数不变，整个曲线也都会被修改，因为它的基函数的定义域是在$t\in [0,1]$ 的整个区间上的。而B样条加入节点，目的就是为了给拟合的曲线增加局部性，从而实现改变一个控制点只会影响整个拟合曲线的一部分，而不会影响整个曲线。而实现的关键就是插入节点，让控制点只能作用到部分节点区间上，而不会作用到整个节点区间上。

贝塞尔曲线的基函数区间定义域是在$t\in [0,1]$ 的，B样条曲线就在这个区间上插入很多节点，从而把整个区间分成很多小的区间。如下图所示，假设我把区间$[0,1]$分成8个子区间，那么我要插入$8+1=9$个节点，假设他们的序号分别是$0-8$。

根据前面B样条曲线的递推公式（这个公式为什么是这样大家就不要追究了，这种结论大佬发现了直接用就行了）：

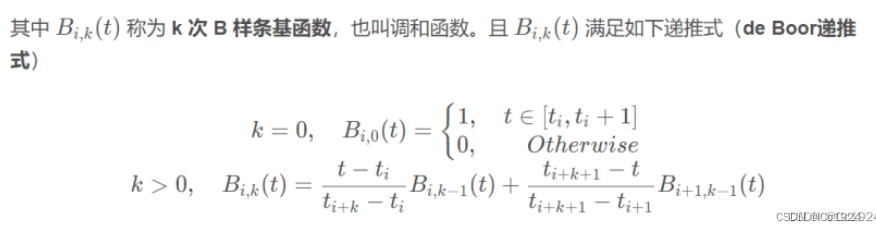
可以发现，在这些节点区间内的基函数都是0次的，也就是他们在各自的区间内都是1，不在自己区间范围内的都是0，并且这个取值和$t$是无关的，所以这个区间内的基函数都是0次的，如下图所示。注意图中的$B_{i,0}$表示的就是当前的样条基函数都是0次的，然后$i$表示的是哪个区间的样条基函数，因为我们有9个点，所以有8个样条基函数，注意下图中的索引都是从0开始的。

那么B样条曲线的递推公式就是在说：可以使用两个相邻的小区间组成一个大区间，同时基函数次数增加1。如下图所示，最开始的子区间里面的B样条函数都是0次的，而由于B样条的递推公式中组合两个相邻区间的时候前面的系数是带有 $t$ 的，而且一个是$t$，另一个是$1-t$（实际公式不是这样，但是也大概是这个思想）。所以组合了两个区间之后，在这个新的区间中的基函数就变成1次的了。同理新区间中的样条基函数$B_i,1$表示样条基函数都是1次的，而$i$表示它的哪个区间的样条基函数。

注意：

• 图中为了方便画图，合并之后的区间和之前的区间长度画成一样大的了，实际上合并之后的区间长度应该是翻倍的。
• 另外图中也是为了方便表示出两个区间合成一个区间的结果，把区间画的而有点问题了。实际上由于第0和第1个区间合成新的区间0，第1和第2个区间合成新的区间1，那么新的区间0和1之间应该是有一般重叠的，但是图中没有把重叠画出来，因为画出来的话就太乱了。如果是正常有重叠的区间的话，那么此时新的区间的基函数应该就是像下图这样也有重叠：
  
  那么如此不断的用B样条的递推公式合并相邻的两个区间的话，可以发现区间个数越来越少，但是区间上的样条基函数的次数会越来越高，如下图所示：

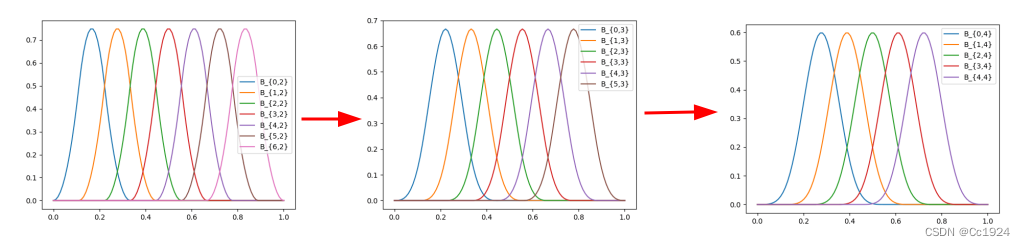
假设我们进行3次这样的区间合并，最终我们得到的每个区间上的样条基函数就是3次的，整个过程如下：

另外也可以看参考视频的讲解中作者给出的PPT，其实也是在表达这个 区间合并、基函数次数递增 的过程：

以上就是B样条曲线的递推公式表示的过程，可以发现其实和前面贝塞尔曲线递推的过程是非常像的，其实都是用相邻的两个点组合成一个新的中间点，然后再用相邻的两个中间点组合成一个更新的中间点，如此迭代……

3.4.B样条引入节点带来的好处——局部性

我们看之前的图，最终我们得到了5个B样条的基函数，并且每个基函数都是3次的。由B样条的公式可以发现，最终我们也需要5个控制点来控制样条曲线，因为控制点的个数和基函数的个数是一样的，因为控制点就是权重，有几个基函数肯定就要有几个权重嘛。

那么我们来分析一下，第0个控制点$P_0$它作用到了几个最初的节点区间上呢？如下图所示，可以发现它之作用到了前4个区间上。也就是说，如果改变控制点$P_0$，最终只会影响在区间$0-4$之间的B样条曲线，而不会影响它后面的B样条曲线，这就是B样条曲线引入控制点之后带来的好处——拟合的曲线具有局部性！不会由于一个控制点的改变而导致牵一发而动全身！

3.5.为什么 m = n + k + 1 ?

首先再次定义以上变量的意思：

• $m$：节点的个数-1，也就是节点的个数=m+1，或者说$m$是节点区间的个数。比如在上图中，节点的个数为9，则$m=8$；
• $n$：控制点的个数-1，也就是控制点的个数=n+1，或者说$n$是控制点区间的个数。比如在上图中，控制点的个数为5，则$n=4$。注意：最后的时候区间是5个，表示控制点个数就是5个，因为每个控制点是作用在一个区间上的；而在节点的那个地方区间是8个，而节点数是9个！
• $k$：基函数的次数，也就是合并区间的最后得到的基函数的次数；

那么为什么 $m=n+k+1$呢？其实从上面合并区间的过程中就可以看出来，每合并一次，基函数的次数上升一次，区间的个数就减少一次。

• 一开始是时候区间的个数就是$m$。
• 最后区间的个数是$n+1$。注意不是$n$，最终的区间个数就是控制点的个数，因为一个控制点对应一个区间的基函数。
• 一共合并了$k$次区间，所以有$m-k=n+1$，因此得到$m=n+k+1$。

注意：既然有上面的公式，到底谁是自变量，谁是因变量？其实从写法就可以看出来，$n$和$k$是自变量，而$m$是因变量。也就是说，控制点的个数$n+1$是自己事先确定的，基函数的次数$k$也是自己事先确定的，确定了这两个之后，选择几个节点$m+1$也自然就确定了，因为这是由B样条曲线的递推公式决定的。

3.6.为什么 阶数(Order) = 次数(Degree) + 1？

首先我们已经明白了**次数(Degree)**的含义，它代表的是最终的基函数的次数，也就是$t$的最高次幂。

那么 阶数(Order) 有什么意义呢？以及为什么满足 阶(Order) = 次(Degree) + 1？

首先说阶数的物理意义：它其实反应了当前的点最多受到几个控制点的控制，也就是如果是4阶的B样条曲线，那么一个点最多受到它周围的4个控制点的控制。

前面我们已经说了，B样条曲线具有局部性，而且分析了为什么具有局部性，本质上是因为区间合并这种操作导致最终基函数所在的区间只能影响到整个节点区间的一部分，所以这个基函数对应的权重（也就是控制点）如果改变，也只会影响到最终拟合的这个区间的样条曲线，而不会影响整个样条曲线。

那么怎么分析的当前的一个点最多受到几个控制点的影响呢？其实也很简单，我们就分析每个控制点覆盖的区间范围，直到某个控制点和第0个控制点没有重合的节点区间。

如下图所示，节点区间$0-1$只受到控制点$P_0$的影响；节点区间$1-2$会受到控制点$P_0$、$P_1$的影响；节点区间$2-3$会受到控制点$P_0$、$P_1$、$P_2$的影响；节点区间$3-4$会受到控制点$P_0$、$P_1$、$P_2$、$P_3$的影响；而到了区间$4-5$的时候，此时前面的控制点$P_0$已经无法施加控制作用了，此时起作用的控制点是$P_1$、$P_2$、$P_3$、$P_4$。

所以可以发现，一个节点区间最多受到几个控制点的控制，和一个控制点可以控制几个节点区间是一样的！那么一个控制点可以控制几个节点区间呢？显然控制点自己就是一个区间，然后每往上走一次，控制点控制的节点区间个数就+1，所以最终一个控制点控制的节点区间个数就是 k+1 ！所以说 阶数 = 次数 + 1。

可以看到就像一种滑窗的感觉，如下图所示：

• 一开始的时候在节点区间开头，只有第0个控制点能发挥作用，滑窗长度是1；
• 慢慢往后遍历节点区间，发挥作用的控制点个数逐渐增加，滑窗长度逐渐变大；
• 从滑动到某个节点区间开始，就只能有恒定个数的控制点发挥作用了，而不会一直增加，也就是滑窗开始保持固定长度，这个长度就是B样条曲线的 阶数(Order) ；
• 快到达节点区间结尾的时候，发挥作用的控制点个数逐渐减少，滑窗长度逐渐变小；
• 最后到达节点区间末尾，只有最后一个控制点能发挥作用，滑窗长度又变成1。

另外从这个图中也可以发现，起始和最后的$k$个区间，也就是阶数-1个区间，有效的控制点个数是不足的，所以一般来说不使用前面的几个节点区间，而使用有效控制点个数到达阶数的那些区间，也就是从中间区间开始使用。

3.7.B样条曲线的特点

• 优点：和Bezier样条一样，B样条也是通过逼近一组控制点来产生的。但是B样条具有两个Bezier样条所不具备的特点：
  （1）B样条多项式的次数可独立于控制点数目（有一定限制）；
  （2）B样条允许局部控制曲线或曲面。
• 缺点：比Bezier样条更复杂。

3.8.B样条曲线的历史

最后给出这个吧，其中前面的B样条曲线的递推公式就是de Boor-Cox公式，1972年就提出来了，真理经久不衰啊……

• 均匀节点意义下的一元B样条(B-splines，Basis Splines缩写)是在1946年由I.J.Schoenberg提出
• 非均匀节点定义的B样条由Curry在1947年提出
• 1962年，法国数学家Pierre Bézier研究了一种曲线，即Bézier曲线
• 1972年，de Boor与Cox分别独立提出了计算B样条基函数的公式，这个公式对B样条作为计算机辅助几何设计(CAGD)重要工具起到了至关重要的作用，称之为de Boor-Cox公式。在此之前，计算B样条基函数大多用差分方法计算，数值上可能不稳定。

4.B样条曲线的矩阵表达式及在SLAM中的应用

参考：均匀B样条曲线的表达式

4.1.均匀B样条的矩阵表达式

注意：这个矩阵形式的推导可以不用关注，实际上是有公式的，在上面的参考博客中就有。只需要知道其中的自变量有$t$和控制点$P$即可。比如在SLAM中，位置样条曲线$P(t)$对$t$求导，得到的就是速度样条曲线，再对$t$求导得到的就是加速度曲线。如果要优化轨迹的时候，那么就是对控制点求导来有优化轨迹。

4.2.均匀B样条表示李群空间的矩阵表达式

4.3.B样条曲线用于SLAM的轨迹表示