$N$ 维超球体体积结论

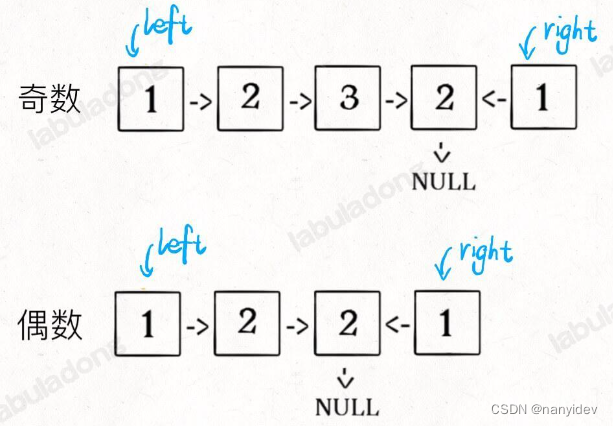
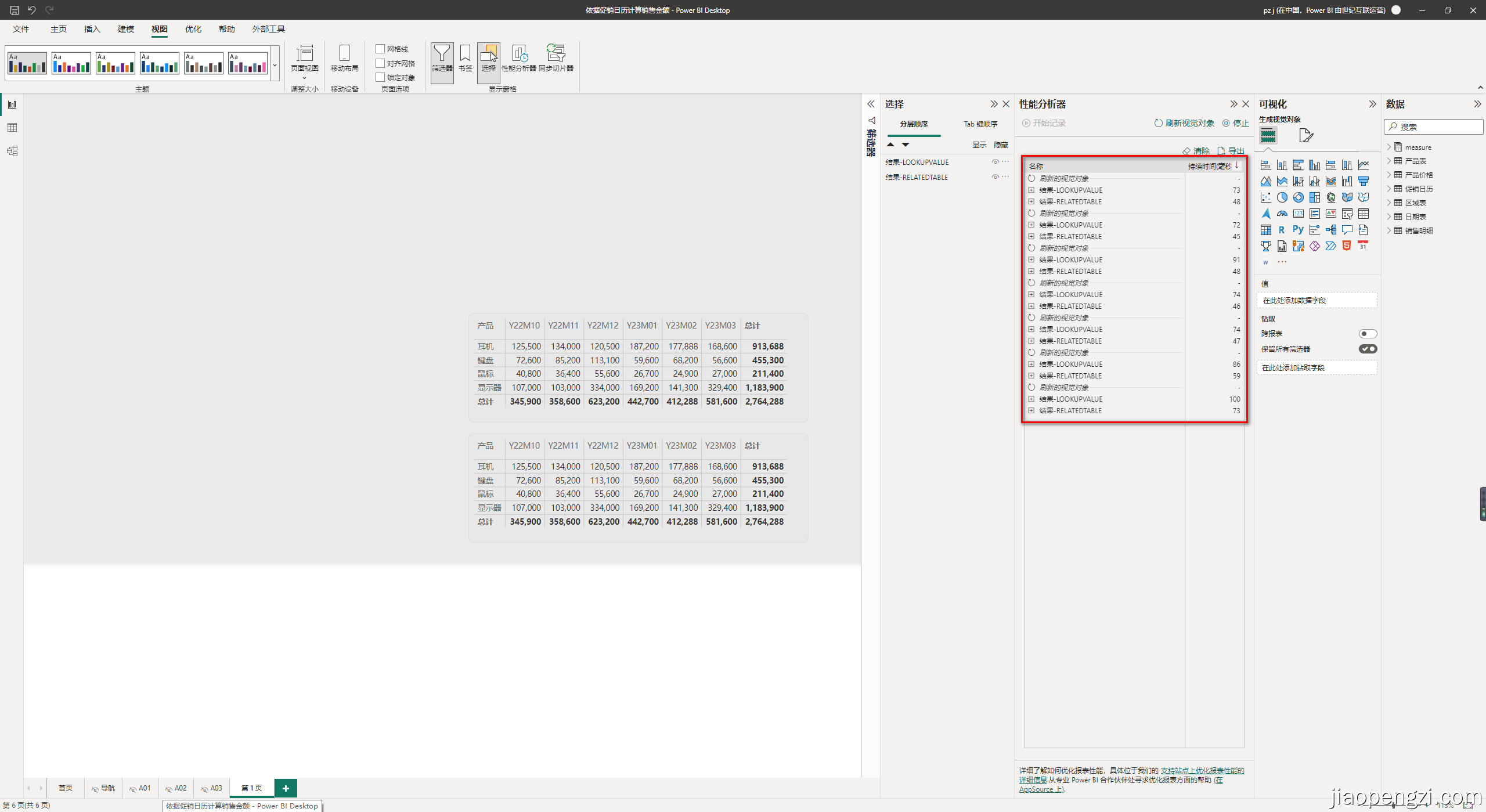
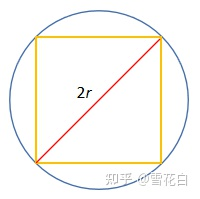
在 $n$ 维空间中，对半径为 $r$ 的超球体（Ball），有 $\mathrm{vol}(\mathcal{B}(0, r)) \geq \left( \frac{2r}{\sqrt{n}} \right)^n$ 。如下图所示，当 $n = 2$ 时，半径为 $r$ 的圆里包含一个边长为 $\frac{2r}{\sqrt{2}}$ 的正方形，圆的直径是正方形的对角线，圆的面积大于正方形的面积。

在这里插入图片描述

闵可夫斯基凸体定理

定理1 在空间 $\mathbb{R}^n$ 中，对任意对称凸体 $\mathcal{C} \in \mathbb{R}^n$ ，若 $\mathrm{vol}(\mathcal{C}) > 2^n$ ，则 $\mathcal{C}$ 必定包含一个非零整数向量。

在这里插入图片描述

注意凸体和凹体的区别
什么是凹多面体，什么是凸多面体，怎么区分，有什么例子？

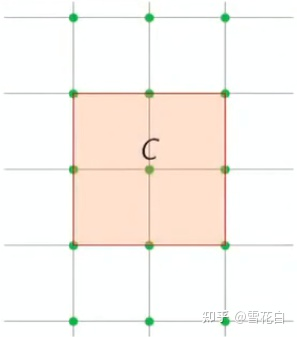
以下图为例，在二维整数格 $\mathbb{Z}^2$ 上，将正方形 $\mathcal{C}$ 的中心放在原点，只要 $\mathcal{C}$ 的面积严格大于 $2^n$ ，那么 $\mathcal{C}$ 必定包含非零整数点（注意是包含在内而非放在边界上）。

证明略（欢迎补充完整证明）。

闵可夫斯基第一定理

虽然在多维空间求解精确的 $\lambda_1$ 很困难，但是存在多项式算法能够快速求解出 $\lambda_1$ 的大致上界。

定理2 对任意 $n$ 维满秩格 $\mathcal{L}(\bm{B})$ ，其第一连续极小满足 $\lambda_1 \leq \sqrt{n} \cdot \mathrm{det}(\mathcal{L})^{1/n}$ 。

证明： 通过对 $\mathbb{Z}^n$ 施加线性变换 $\bm{B}$ 可以得到对应的格 $\mathcal{L}$ ，即 $\mathcal{L} = \bm{B} \mathbb{Z}^n$ 。

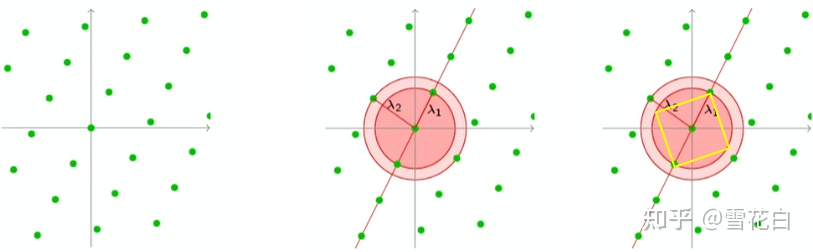
在这里插入图片描述

图上图为例，在格 $\mathcal{L}$ 上找到以格点为球心、半径为 $\lambda_1$ 的超球体 $\mathcal{B}(0, \lambda_1)$ ，该超球体内包含一个体对角线长为 $2\lambda_1$ 的立方体 $\mathcal{S}$ ，有 $\mathrm{vol}(\mathcal{S}) = \left( \frac{2\lambda_1}{\sqrt{n}} \right)^n$ 。

对立方体 $\mathcal{S}$ 施加逆变换 $\bm{B}^{-1}$ 转回到 $\mathbb{Z}^n$ 上得到一个凸体 $\mathcal{C}$ 。

易知， $\mathrm{vol}(\mathcal{C}) = \mathrm{det}(\bm{B}^{-1}) \cdot \mathrm{vol}(\mathcal{S}) = \mathrm{det}(\mathcal{L})^{-1} \cdot \left( \frac{2\lambda_1}{\sqrt{n}} \right)^n \leq 2^n$ 。否则的话，有 $\mathrm{det}(\bm{B}^{-1}) \cdot \mathrm{vol}(\mathcal{S}) > 2^n$ ，由 $n$ 维超球体体积结论进一步有 $\mathrm{det}(\bm{B}^{-1}) \cdot \mathrm{vol}(\mathcal{B}(0, \lambda_1)) > 2^n$ ，即超球体 $\mathcal{B}(0, \lambda_1)$ 逆变换后的对称凸体会严格把一个非零整数点包含在内而不是放在边界上，这就与 $\lambda_1$ 的定义冲突了。

换算一下，得到 $\lambda_1 \leq \sqrt{n} \cdot \mathrm{det}(\mathcal{L})^{1/n}$ 。

证毕。

闵可夫斯基第二定理

定理3 对任意 $n$ 维满秩格 $\mathcal{L}(\bm{B})$ ，有 $\lambda_1 \leq \left( \prod_i \lambda_i \right)^{1/n} \leq \sqrt{n} \cdot \mathrm{det}(\mathcal{L})^{1/n}$ 。