一、公式及符号约定

这篇论文是将直接法的残差计算从点扩展到了线段，所以一些符号在第三章的部分提前做了约定。用Π表示投影的函数，也就是用像素坐标和内参矩阵以及深度信息，投影出点的空间坐标，反之Π-1表示的是将空间坐标投影到像素平面上。由此可以定义特征点的投影过程：

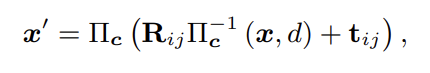
利用这个式子，我们可以得到前一帧上特征点投影到当前帧上的位置，用这个位置，就可以计算直接法中的光度误差：

14讲里面对光度误差的定义没有这个式子这么复杂，这个式子中引入了Ii、Ij、ai、aj、bi、bj这些表示仿射光照变化的参数，所以计算出来的光度误差是更加准确的，wx是一个权重，权重的取值与梯度值有关。通过这个式子，我们可以计算一个点的光度误差。

除了点的光度误差，这一章节还补充了线段的普朗克坐标，关于普朗克坐标，之前的博客中有总结，这里不再赘述。但是不同之处在于，这篇文章中的普朗克坐标做了一下归一化处理，原本的普朗克坐标是两个向量组成：线段的方向向量以及光心、线段组成平面的法向量，在这篇论文中对普朗克坐标的定义稍微改变了一下：

而一般的普朗克坐标定义是：d=p2−p1,m=p1​×p2，也就是完全依赖于线段的两个端点，不过论文中的定义并不妨碍我们用普朗克坐标去对线段进行表示，经过验算其实这两种表达方法都是一样的。在普朗克坐标的基础上，可以用点的坐标和线段的普朗克坐标直接计算出点到空间线段的距离：

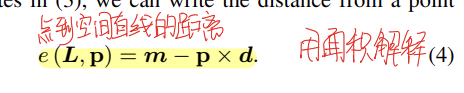
这个式子其实用面积取解释是最好理解的，这里我用最原始的普朗克坐标定义去解释，组成普朗克坐标的两个向量，d表示线段的方向，m的大小为围成三角形的面积的两倍，d的方向是围成平面的法向量方向。我们假设相机光心为o，线段的两个端点为p1p2，点为p，那么有下面的图：

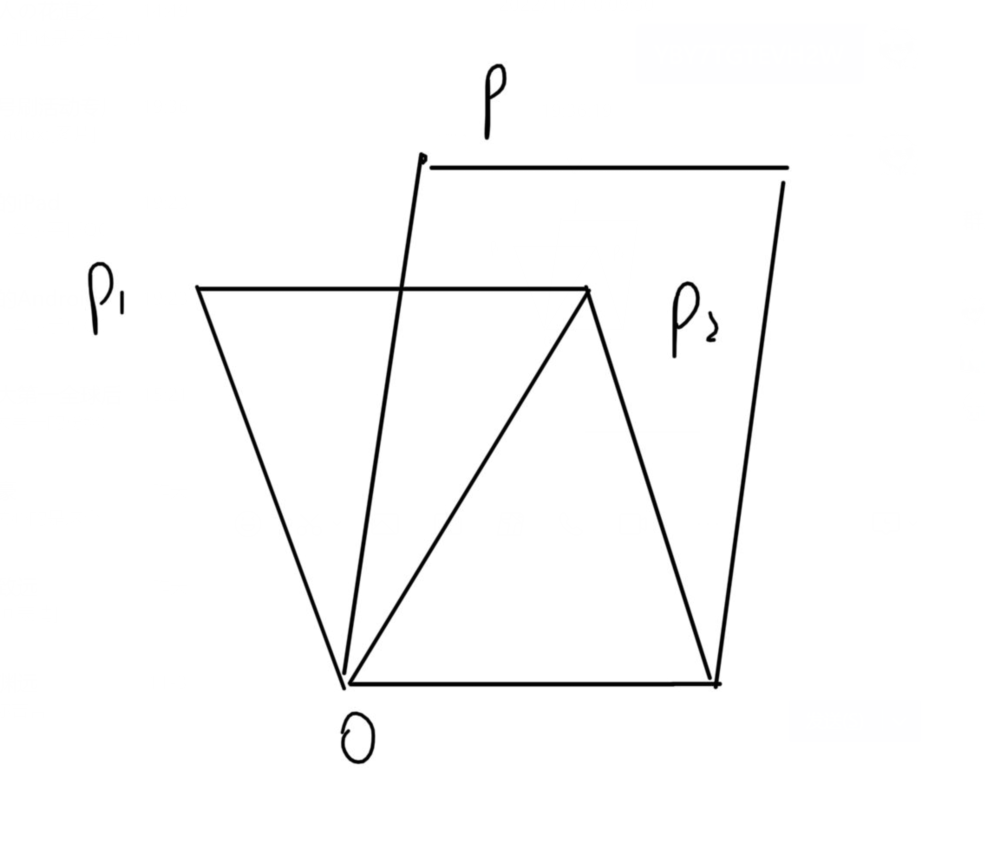
对于这个图来说，L也就是空间线段P1P2，m的大小表示的是三角形OP1P2的面积的两倍，也就是图中矮一点的平行四边形的面积，而p也就是向量OP，其与d叉乘的，也就是OP与P1P2叉乘，其大小表示的是图中较高一点的平行四边形的面积，而这两个面积，底的大小是一样的，差别就是高，而这个高，反应的就是p到p1p2的距离。这里可能存在一些式子细节上的理解问题，但是个人感觉这样去解释是最方便的。

二、基于点线的直接法

A、线段上任一点的空间表示方法

对于一帧图像上的一条线段，两个端点的坐标可以用投影和逆深度来表示（论文没有提逆深度是怎么得到的，应该是用三角化）：

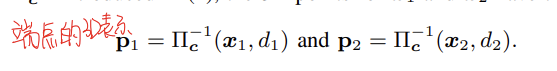
利用这两个点，可以计算出线段的普朗克坐标：

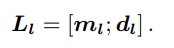
那么对于2D线段上的任何一点，定义点的方向向量为：

这个定义看起来比较麻烦，从图里来看直接就是相机光心发出，经过点x的向量：

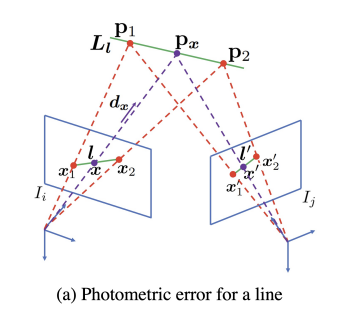
在定义这些量之后，我们可以得出下面的式子：

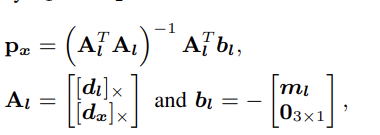
先说结论，通过推导，这个式子表明线段上任何一个点的空间坐标依赖于线段端点的逆深度。推导的过程在论文的附录里面，推导的过程其实不难，对于点的空间坐标px，由于px必然在线段p1p2上，所以点到线段的距离一定是0，此外p1px和p1p2一定是共线的，由此可以写出下面两个式子：

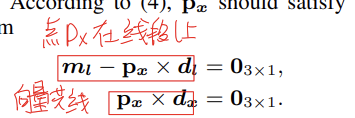
用[]表示向量的反对称矩阵形式，那么上面的式子可以整理为：

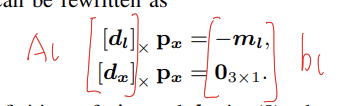
B、线段的光度误差计算

线段的光度误差可以分为两部分：端点的光度误差和线段上采样点的光度误差。

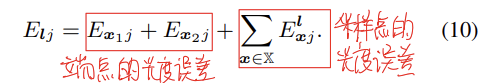
由于我们在上一节最后证明了，线段上任何一点的光度误差只取决于端点的逆深度，所以对于上面这个式子，其结果只取决于两个端点的逆深度。

C、线段的共线约束

论文中使用的线段提取方法是LSD，而LSD本身存在的问题是受到运动模糊或者取整的影响，线段提取本身存在一定的不确定性，不确定性反应在线段的宽度上。这里个人理解是线段可能并不准确，会由于抖动、模糊等原因，让坐标不准确，也就是说提取出来的一条线段，其周围一定范围可能仍然属于这条线段。基于此，论文对线段增加了一个支持域，支持域宽度用ρ表示，以此来衡量线段的不确定性，ρ越大，说明线段提取结果周围很大的范围都可能是线段的一部分，所以不确定性大。

所谓共线约束，实际上就是指一条线段在所有观测到的图像上检测的2d线段，反过来投影其端点应该保持共线，利用这一点，可以写出公式：

D、完整的残差公式

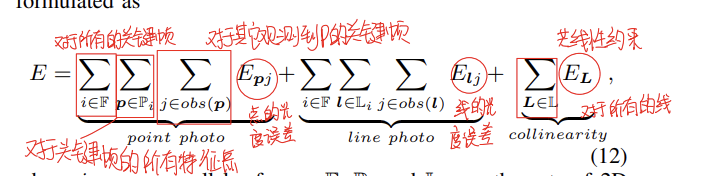
完整的残差公式被定义为上式，可以简单分为三部分：特征点的光度误差、线段的光度误差以及线段的共线约束。

E、基于滑动窗口的优化策略

这篇论文采用了VINS同样的滑动窗口机制，目的是为了提高残差公式的优化效率以及准确性，优化的目标包括位姿和点线坐标。优化的细节论文没有明说，是直接参考了另一篇论文的内容。

F、两步优化策略

为了加速优化的速度，论文还补充了两步的LM优化，没太看明白，个人理解是将变量拆成两部分做优化，先优化线的坐标，之后固定线的坐标，优化位姿和逆深度信息。

三、前端

这一章论文介绍了3D线段的初始化以及2D线段的合并。线段的初始化部分，由于采用的是直接法，所以对于当前帧并没有进行特征提取的过程，所以使用的是一种跟踪策略，具体来说是先对线段上的点进行采样，每个采样点进行投影，投影得到的点拟合一条2D线段，之后利用两条线段的反向延长曲面，相交得到一个3D线段，从而完成初始化的过程。但是问题在于，这个初始化执行的时机，从这个初始化的过程可以看出，跟踪准确的前提是要一个准确的位姿，否则投影拟合出来的线段是不准确的，但是前面计算位姿的时候明明是有线段的对应关系的，这二者相互冲突了，这里看的不是很明白，因为论文是在同一作者上一篇论文中改进的，之后会查一下上一篇文章，也就是DPLVO，看看里面是怎么写的。

2D线段的合并这里个人看的也不是很清楚，论文说LSD提取出来的线段有时候许多断掉的小线段，如果直接合并，可能会让本来的两条线段误合并成一条，这显然是不合适的。

所以在这里论文提出了一些新的合并措施：