题目：剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣（Leetcode）

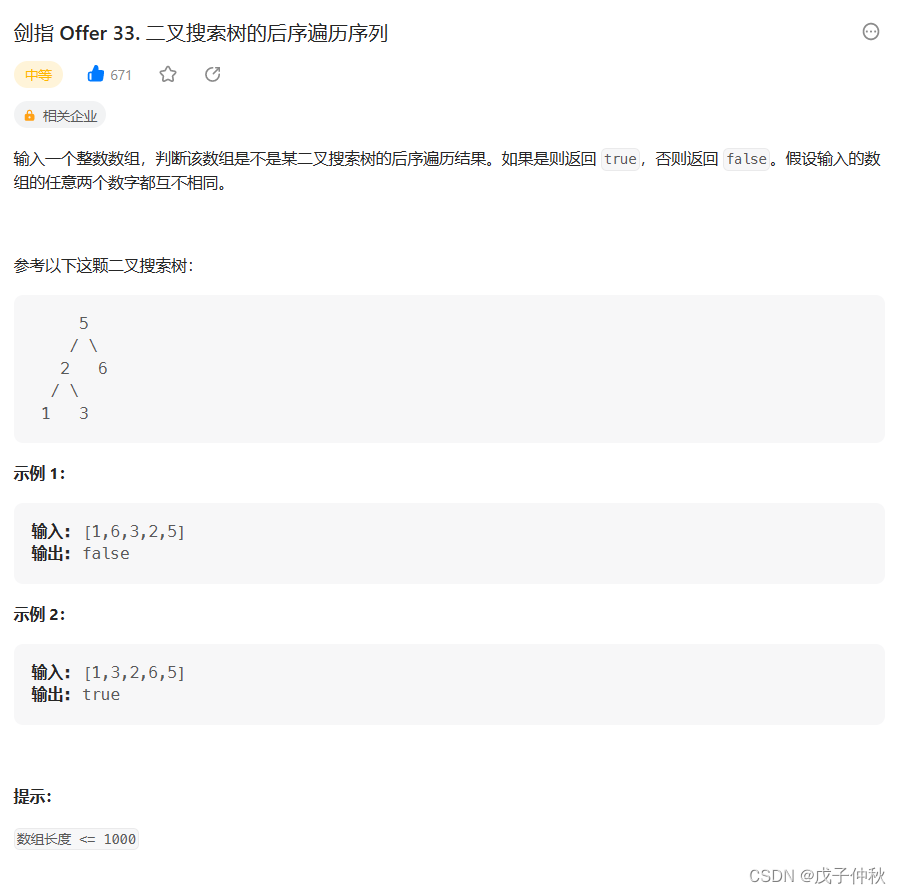
题目的接口：

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        
    }
};

解题思路：

我一般做二叉树的遍历的题目，

用的都是递归法，

这里二叉搜索树有一个特点：左子树小于根节点，右子树大于根节点

我们就利用这个特性来判断数组是不是二叉搜索树的后序遍历。

大体思路就是判断：

左子树是否小于根节点，右子树是否大于根节点，

遍历过程中找到左子树和右子树的边界，

再以每个左子树和右子树作为子集，

递归遍历每一个子集，如果符合条件就返回 true，不符合就返回 false。

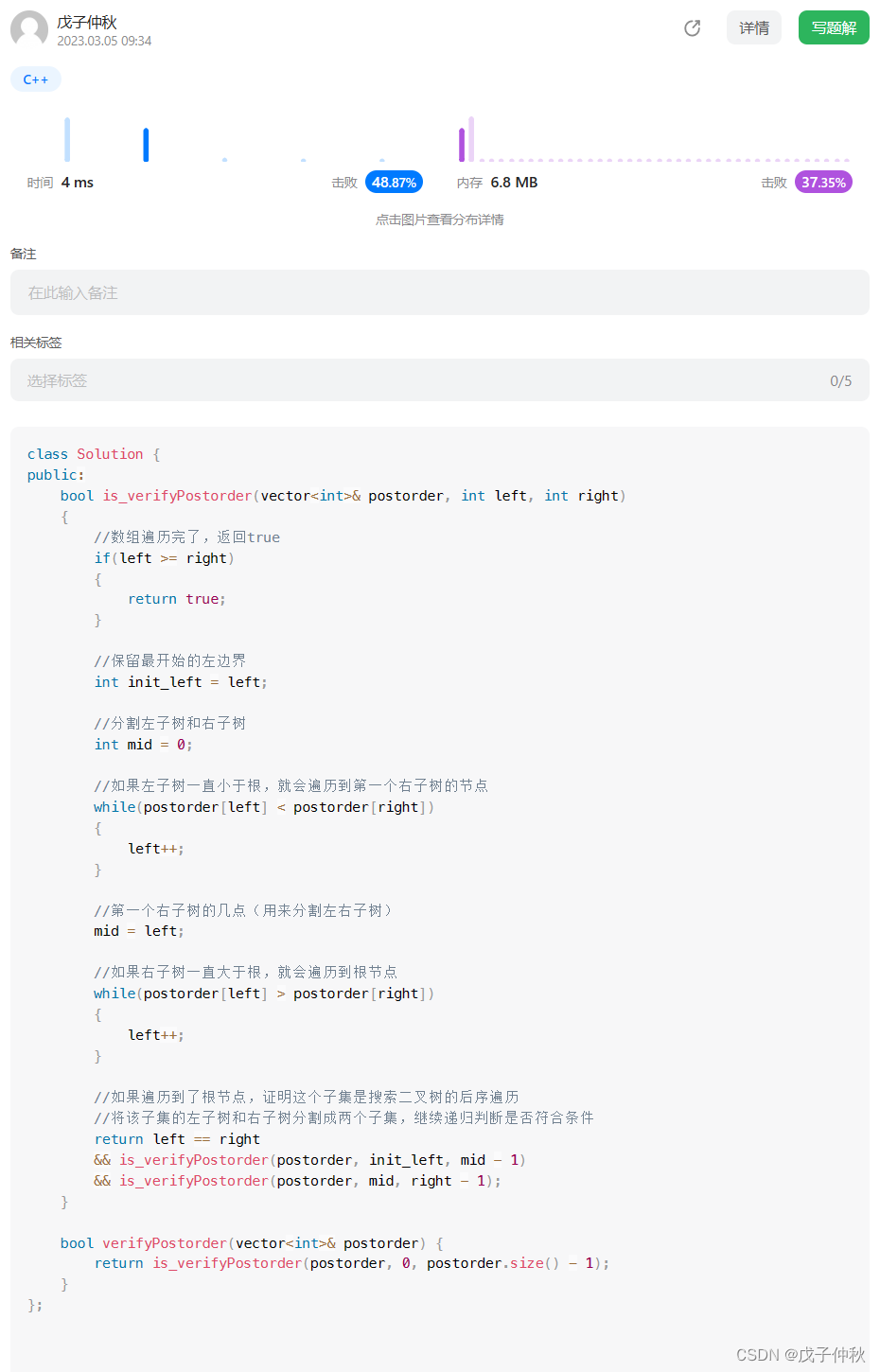
代码：

class Solution {
public:
    bool is_verifyPostorder(vector<int>& postorder, int left, int right)
    {
        //数组遍历完了，返回true
        if(left >= right)
        {
            return true;
        }

        //保留最开始的左边界
        int init_left = left;

        //分割左子树和右子树
        int mid = 0;

        //如果左子树一直小于根，就会遍历到第一个右子树的节点
        while(postorder[left] < postorder[right])
        {
            left++;
        }

        //第一个右子树的几点（用来分割左右子树）
        mid = left;

        //如果右子树一直大于根，就会遍历到根节点
        while(postorder[left] > postorder[right])
        {
            left++;
        }

        //如果遍历到了根节点，证明这个子集是搜索二叉树的后序遍历
        //将该子集的左子树和右子树分割成两个子集，继续递归判断是否符合条件
        return left == right 
        && is_verifyPostorder(postorder, init_left, mid - 1)
        && is_verifyPostorder(postorder, mid, right - 1);
    }

    bool verifyPostorder(vector<int>& postorder) {
        return is_verifyPostorder(postorder, 0, postorder.size() - 1);
    }
};