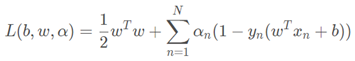Edge cut and Vertex cut

图结构描述了数据流动，分布式图计算系统或核外图计算系统均依赖于图划分。
良好的图划分策略可以最小化通信和存储开销，并确保计算平衡。
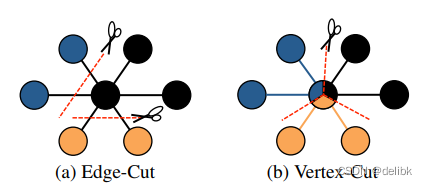
请添加图片描述

Edge cut

如下图所示，Edge cut 将节点分配到不同的机器，边横跨各机器，通信开销和存储开销直接与切割的数量呈比例.因此需要通过最小化边的切割数目，将节点尽量多的分给机器来减少通信开销和确保计算平衡。
但是规模巨大的图想要计算出一个最优的切割会付出巨大的花费，因此大多数都采用了随机切割，随机将节点分配给机器。随机的切割工作的时候接近最佳情况下的平衡，但是这也消耗了最坏的通信花费，切割了最多的边。
定理：如果节点被随机分配给p个机器，那么edge cut 的 expected fraction 为：

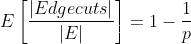
对于一个exponent 为 \partial的 power-law graph 每个节点期望的edge cut 为：

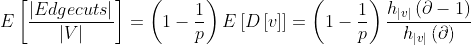
注：power-law degree distributios原来是一种描述网络图中结点度的分布，中文可叫做“幂律度分布”。

每次边的切割都会在本地保存一个邻近节点的备份，因此会增加网络和存储开销。
如图所示，切割成三份，增加了7个节点副本，每个节点都被复制了至少一次。
任何节点或边的变化都会通过网络同步到其他机器。

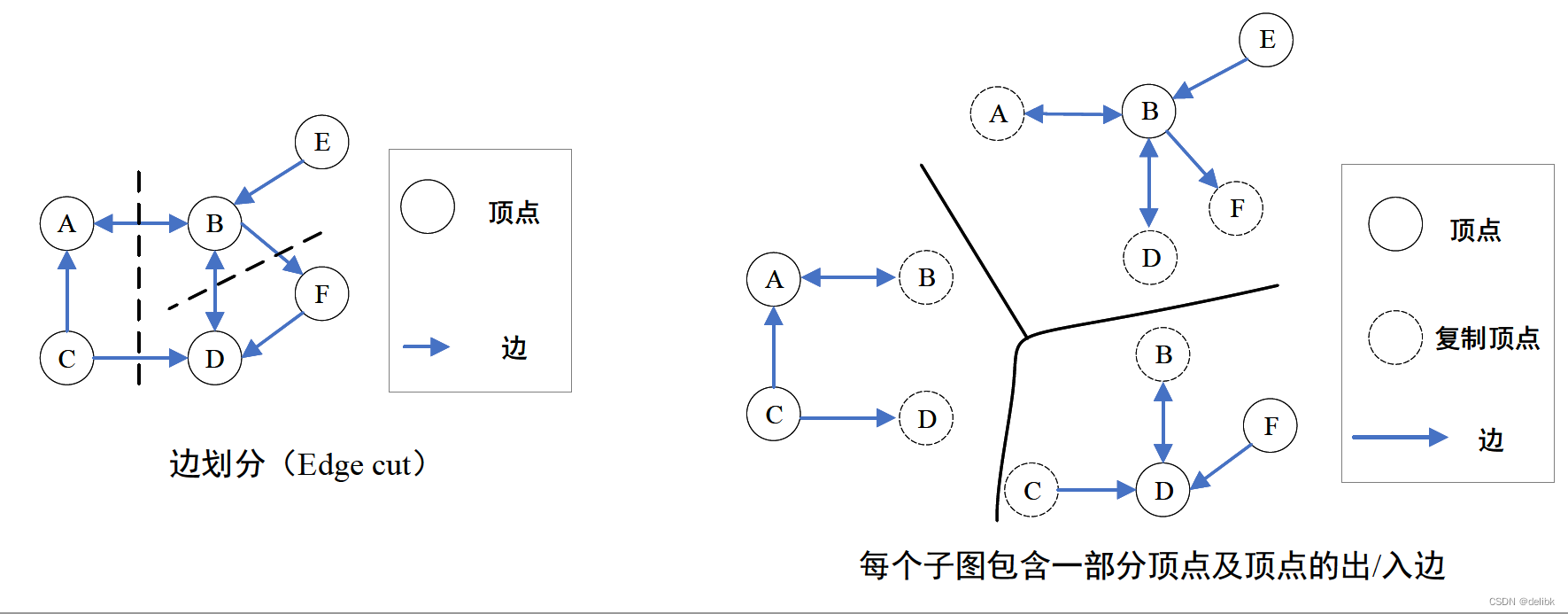
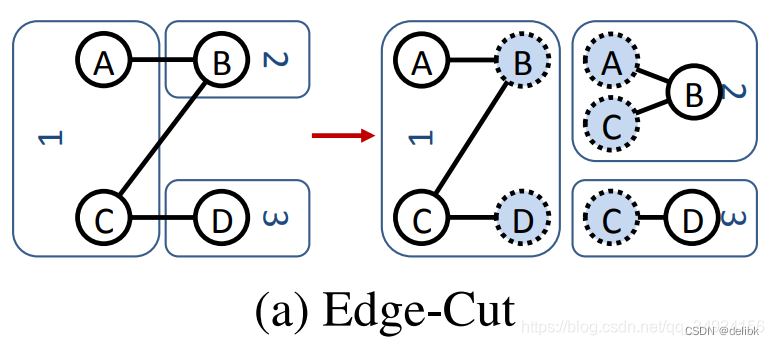
请添加图片描述

如上图所示，切割成三份，增加了5个节点副本，每个节点都被复制了至少一次。

对于频繁遍历的边，应该减少cut edge的存在，从而减少跨设备间的通信，提高查询效率。即把进行遍历的相邻顶点放在相同的分区，减少通信消耗。

顶点的id分配：一个分区就是一个有序的id区间，顶点被分配到一个分区就会为该顶点分配一个id，也就是顶点的id决定了该顶点属于哪一个分区。给一个顶点分配id：JanusGraph就会从顶点所属分区的id范围中选一个id值分配给该顶点。(先定分区，在分配id)

为顶点确定分区：JanusGraph通过配置好的 placement strategy来控制vertex-to-partition的分配。

默认策略：在相同事务中创建的顶点分配在相同分区上。
缺点：如果在一个事务中加载大量数据，会导致分配不平衡。
定制分配策略：实现IDPlacementStragegy接口，并在通过配置文件的ids.placement项进行注册。

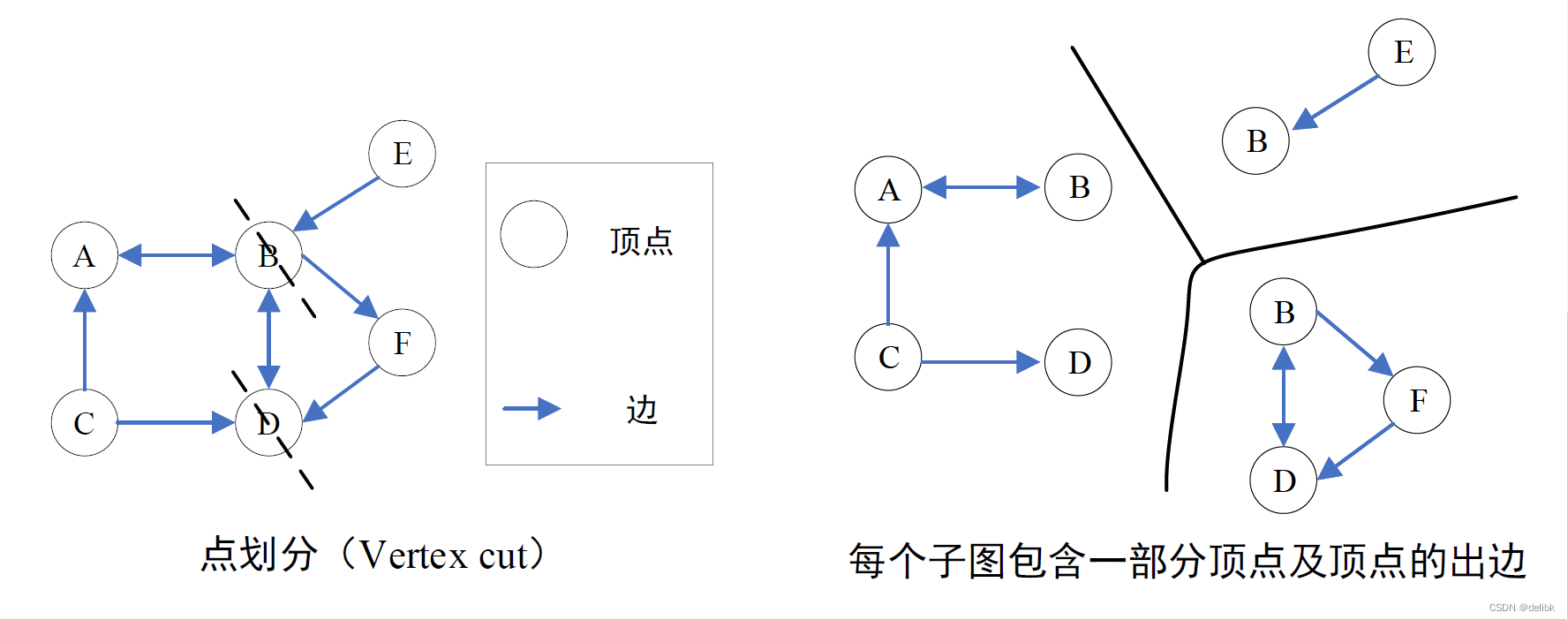
Vertex cut

顶点切割，即把一个顶点进行切割，把一个顶点的邻接表分成多个子邻接表存储在图中各个分区上。
如图所示，vertex cut将边分配给不同机器，允许节点跨不同机器，节点的变化都需要同步到其他机器上，故通信开销与存储开销与每个节点跨机器的数呈正比，因此我们需要最小化每个节点跨机器的数。
比起edge cut，vertex cut 从理论和实践上，都显示出更好的性能。
请添加图片描述
通过为边定义一个hash函数,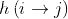

可以保证每个节点最多在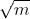在这里插入图片描述个机器上（m为机器集群的数量）。

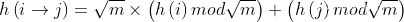
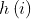是一个在节点ID上统一hash函数。

对于一个均衡的 p-way vertex cut ，将边集合分配给机器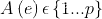，节点横跨机器集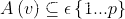，因此可定义均衡切割如下所示：

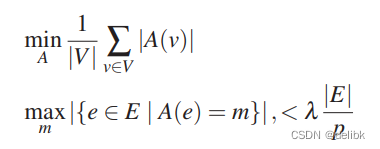
平衡因子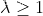是一个很小的常量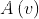，里的每一个机器都将会有一个节点v的副本，每次节点的修改会传到每个副本，
因此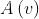的大小将会影响通信开销。
随机将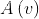中的一个副本设为master，维持着节点的主版本，其他副本都从此节点上复制。

vertex cut 能够更好的作用在power-law graph，通过切割部分度非常高的节点就能将整个图切分。同时每条边都保证了只存在于一个机器上。

在真实的大规模图上，Vertex cut 找到一个最优的切割也会付出巨大的花费，但是《Powergraph: Distributed graph-parallel computation on natural graphs》里为边的分区提出了几个简单的启发式data-parallel算法。最简单的策略就是随机的将边分给机器，随机的vertex cut 比随机的edge cut 更有效果，随机切分也能几乎达到最优均衡。

在集群数为p时，随机切割期望副本为：

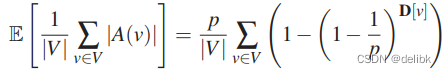
对于power-law graph来说，副本期望由power-law 常量\alpha决定：

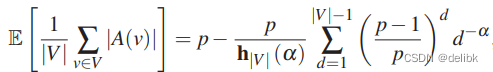
其中：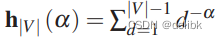

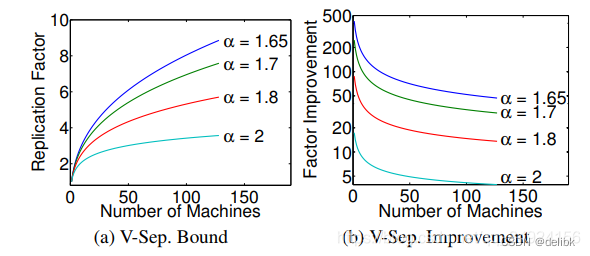
从上图（a）可以看到，虽然越小（度很高的节点越多），replication factor越大，但是相对于edge cut，vertex cut的有效增益实际上随着α的降低而增加。图（b）显示的是随机edge cut的期望花费与随机vertex cut的期望花费，显示出了使用vertex cut的数量级增量。

对于一个给定的edge cut 有 g个镜像副本，使用 vertex cut 进行分区能使副本的数量少于g。

目的：一个拥有大量边的顶点，在加载或者访问时会造成热点问题。Vertex Cut通过分散压力到集群中所有实例从而缓解单顶点产生的负载。
方法：JanusGraph通过label来切割顶点，通过定义vertex label成partition，那么具有该label的所有顶点将被分配在集群中所有机器上。
案例：对于product和user顶点，product顶点应该被定义为partition，因为用户和商品有购买记录（edge），热销商品就会产生大量的购买记录，从而会造成热点问题。

改进Vertex cuts随机分配算法：

这是一顺序贪心启发式算法，能使边在不同的机器上从而最小化conditional expected replication factor。

现假设在放置边i后，任务是放置边i+1，定义conditional expectation如下：

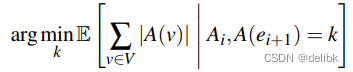
Ai是前一个边i的分配。使用前面得到的定理，对于边我们可以有以下规则：

如果A(v)与A(u)相交，那么该边(u,v)应存于交集的机器中。
如果A(v)与A(u)不为空并且没有交集，应该将该边分给节点中最多边未分配边的那个节点的A(i)中的任意机器。
如果一个或着两个vertex已经被分配，那么选择被分配了节点的机器。
如果两个节点都没被分配，那么将边分给负载最小的机器。

Vertex cut as table

GraphX resilient distributed graph (RDG)数据结构在vertex cuts 实现时将其分为三个无序平行的表。
分别如下所示: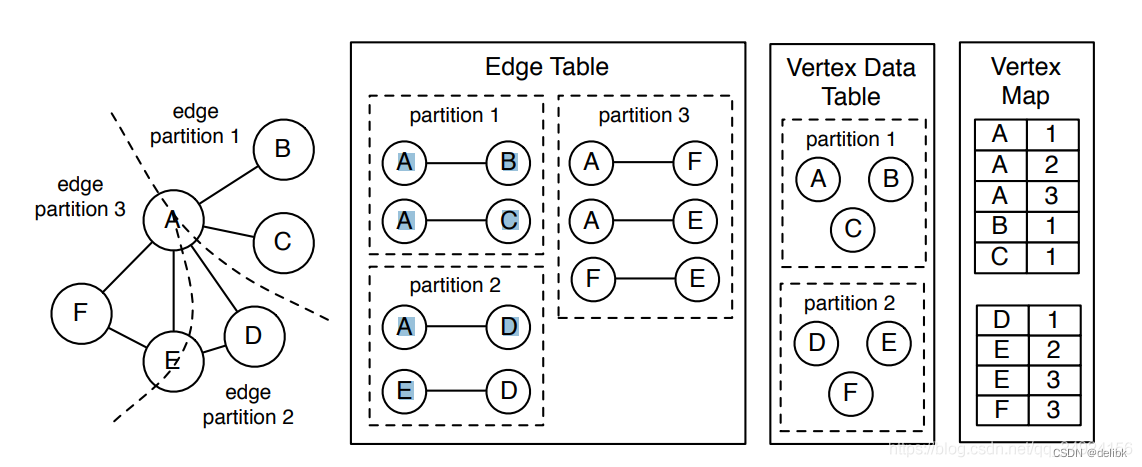 在这里插入图片描述
EdgeTable(pid, src, dst, data)，存储相邻结构以及边的数据。（pid 表示分区编号，src 表示起始节点，dst 表示结束节点）这个表只包含节点的id，不包含节点数据。依据pid 分区。

VertexDataTable(id, data)，存储节点的数据，由 vertex id 进行分区。
VertexMap(id, pid)，显示了节点ID和邻接边的虚拟分区的映射。此表通过vertex id进行分区。

The partitioner is a hint to Spark to ensure the join site would be local to the edge table. This allows GraphX to shuffle only the vertex data and avoid moving any of the edge data.

vertex data table 与 vertex map table 可以组合为一个表，但是因为他们的功能不同，所以将其划分为了两个表。vertex data table 包含与在图形计算过程中发生变化的顶点的相关状态，vertex map table 保留了静态的图结构.