1 简介

朗道-西格尔零点猜想（the Landau-Siegel Zeros Conjecture），是一个数学难题。

要理解朗道-西格尔零点猜想，首先需要理解黎曼猜想，进而需理解广义黎曼猜想，以及狄利克雷L函数。断言L函数没有异常零点（西格尔零点）的猜测就被称为Landau-Siegel猜想。

2 黎曼猜想

可以参见我以前写的文章：
黎曼猜想简介：https://blog.csdn.net/zephyr_wang/article/details/125340716

在实数范围内，黎曼函数如下表示，在实部大于1下，黎曼函数才收敛。可以看到与下面的L函数很类似。

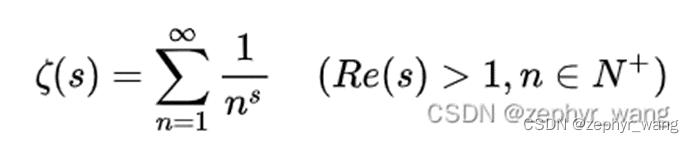
3 广义黎曼猜想

狄利克雷在1831年为了证明狄利克雷定理而引进狄利克雷L函数。

狄利克雷L函数下的广义黎曼猜想最初可能是由皮尔茨（Piltz）于1884年提出的。与原始的黎曼猜想类似，该猜想对研究素数分布十分重要。

如一个已知的狄利克雷特征χ，可以定义如下狄利克雷L函数。

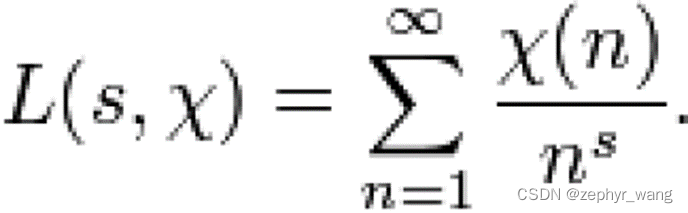
其中，s为实部大于1的所有复数。这一函数可以解析延宕为整个复平面上的亚纯函数。

广义黎曼猜想（generalized Riemann hypothesis，GRH）即是指，狄利克雷L函数L(χ,s)的所有非平凡零点的实部都为1/2。
当对所有n都有χ(n) = 1时，广义黎曼猜想退化为普通的黎曼猜想。

4 狄利克雷特征

狄利克雷特征是一种算术函数，它用来定义L函数。两者都是由狄利克雷在1831年为了证明狄利克雷定理而引进。

狄利克雷特征是一个定义在整数上，值域为 C 的函数 χ ,满足:

1. χ(n+N)=χ(n) (N>0为一整数常数)
2. χ(1)=1
3. χ(nm)=χ(n)χ(m)
4. χ(x)=0(gcd(x,N)≠1)

只要满足以上四条就是一个狄利克雷特征，狄利克雷特征不唯一。
gcd(greatest common divisor)又称辗转相除法,用于计算两个整数a,b的最大公约数

5 狄利克雷L函数

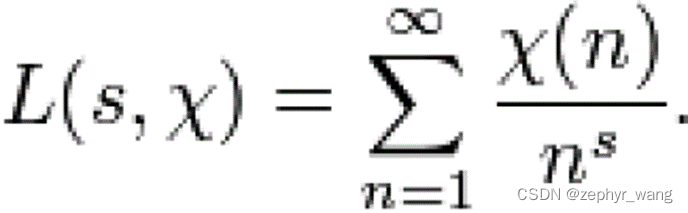
6 狄利克雷定理

狄利克雷（1805～1859）　Dirichlet，Peter Gustav Lejeune　德国数学家。对数论、数学分析和数学物理有突出贡献，是解析数论的创始人之一。

狄利克雷定理:也称为狄利克雷素数定理，是数论领域的定理。指对于任意两个互质整数a和d，存在无限多个形式为a+nd的素数，其中n是正整数。

狄利克雷定理拓展了欧几里得定理（欧几里得定理指出有无穷多个素数）。

如a为3，d为4，3与4互质，存在无穷多个素数（质数）：3+n4，如下：
3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83, 103, 107, 127, 131, 139, 151, 163, 167, 179, 191, 199, 211, 223, 227, 239, 251, 263, 271, 283, …
其中n等于如下内容：
0, 1, 2, 4, 5, 7, 10, 11, 14, 16, 17, 19, 20, 25, 26, 31, 32, 34, 37, 40, 41, 44, 47, 49, 52, 55, 56, 59, 62, 65, 67, 70, 76, 77, 82, 86, 89, 91, 94, 95, …

关于狄利克雷怎么引入狄利克雷特征和L函数，来证明狄利克雷定理，就暂时不多解释了。

7 朗道-西格尔零点猜想

广义黎曼猜想认为所有L函数的“非平凡零点”都位于一条特定的直线上（即猜测所有L函数的非平凡零点都位于实部为1/2的直线）。

但可惜的是朗道（Landau）发现一些特殊情况下，L函数的“非平凡零点”就是可能会出现在我们要的区域外（我们称呼它为“异常零点（西格尔零点）”）。

因为Landau和Siegel两位数学家在L函数异常零点这个领域里做了开创性的工作，所以异常零点也常常被称为Landau-Siegel零点。而断言L函数没有异常零点（西格尔零点）的猜测就被称为Landau-Siegel猜想。

所以广义黎曼猜想恰好是Landau-Siegel猜想的充分条件，即广义黎曼猜想可以推导出Landau-Siegel猜想，而Landau-Siegel猜想推导不出广义黎曼猜想。

8 张益唐的新结果

从上面情况看，张益堂让Landau-Siegel猜想的证明更近了一步。

参考：

1. 狄利克雷定理简述：https://zhuanlan.zhihu.com/p/578435248
2. Dirichlet’s theorem on arithmetic progressions:
   https://encyclopedia.thefreedictionary.com/Dirichlet%27s+theorem+on+arithmetic+progressions
3. 什么是朗道-西格尔零点猜想？https://www.zhihu.com/question/360965839
4. 张益唐教授作学术报告 分享朗道-西格尔零点猜想相关工作https://baijiahao.baidu.com/s?id=1749072052316772845&wfr=spider&for=pc