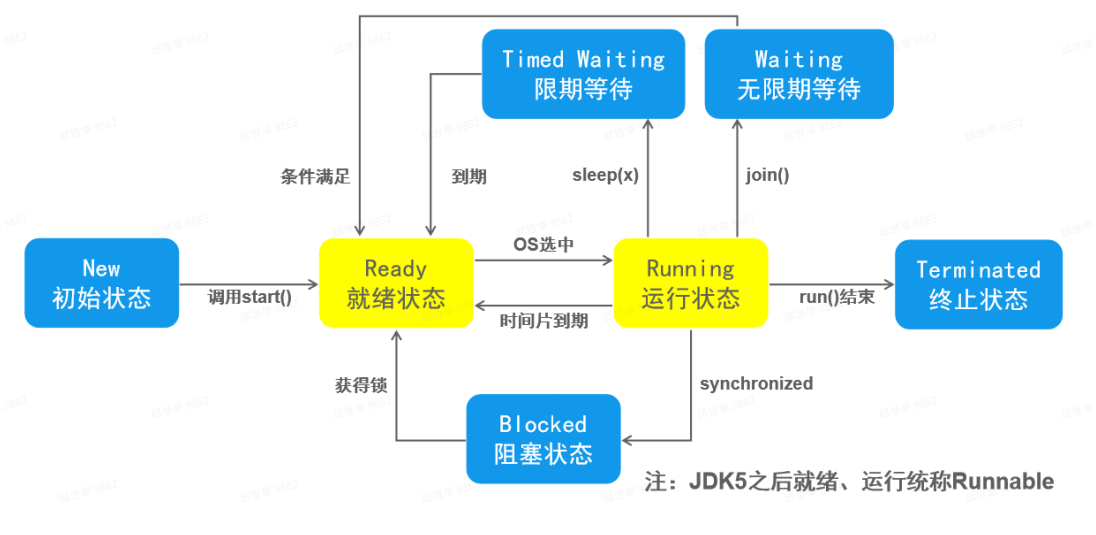
on-policy的定义：behavior policy和target-policy相同的是on-policy，不同的是off-policy。

behavior policy：采样数据的策略，影响的是采样出来s,a的分布。
target policy：就是被不断迭代修改的策略。

如果是基于深度的算法，那么非常好分辨：目标函数里面一定有s和a的期望，而计算梯度的时候使用了SGD，把一个采样作为了期望的值。但是这里面还有一个隐含的限制就是采样遵循的分布必须是s,a的分布。

因此分辨是否是on-policy的，只需要看目标函数。如果目标函数中s,a的分布和策略相关的，那么一定是on-policy的，如果是策略无关的，那么一定是off-policy的。

比如DQN的目标函数：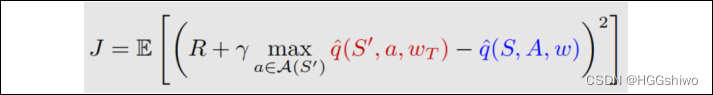
这里一个(s,a)对看成一个随机变量，服从均匀分布，因此分布和策略无关（至于为什么s,a是均匀分布，那个是算法自己假设的），因此采样的时候需要用到experience replay，使得不管什么策略采样得到的reward，都变成均匀分布的。

因此用了experice replay之后，随便什么策略采样，虽然采样出来s,a服从那个策略的分布，但是经过experice replay之后还是变成了均匀分布。

比如PG:

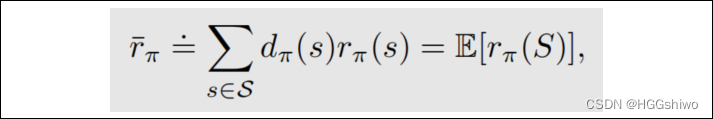
这里面的随机变量是s, 而s是服从stationary distribution，就是agent出现在这个state的次数形成的分布。而这个分布和策略pi是相关的，因此是on-policy的(改变策略之后，agent出现的概率也改变了)

比如DPG:

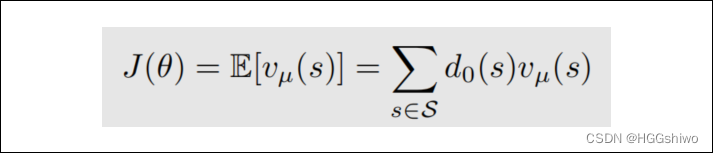
这里面的分布d是一个常数(这是为了计算梯度方便)，因此DPG中s,a的采样和策略无关，是off-policy的。

比如PPO:

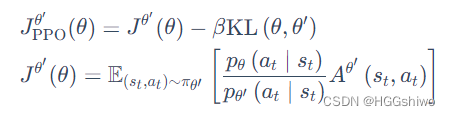
就是一个期望+一个类似正则项的东西，而非常明显看出来，这个期望是服从策略theta’的，也就是说s,a分布和策略相关，因此是on-policy的。

简单说下PPO：PPO用两个网络表示策略，一个是theta’一个是theta，用theta’网络的策略采样reward，得到的reward给theta的网络梯度下降。看起来怎么用了两个策略? 其实两个策略最后慢慢收敛到一起的，是一个策略。如果是off-policy是完全和策略无关的。