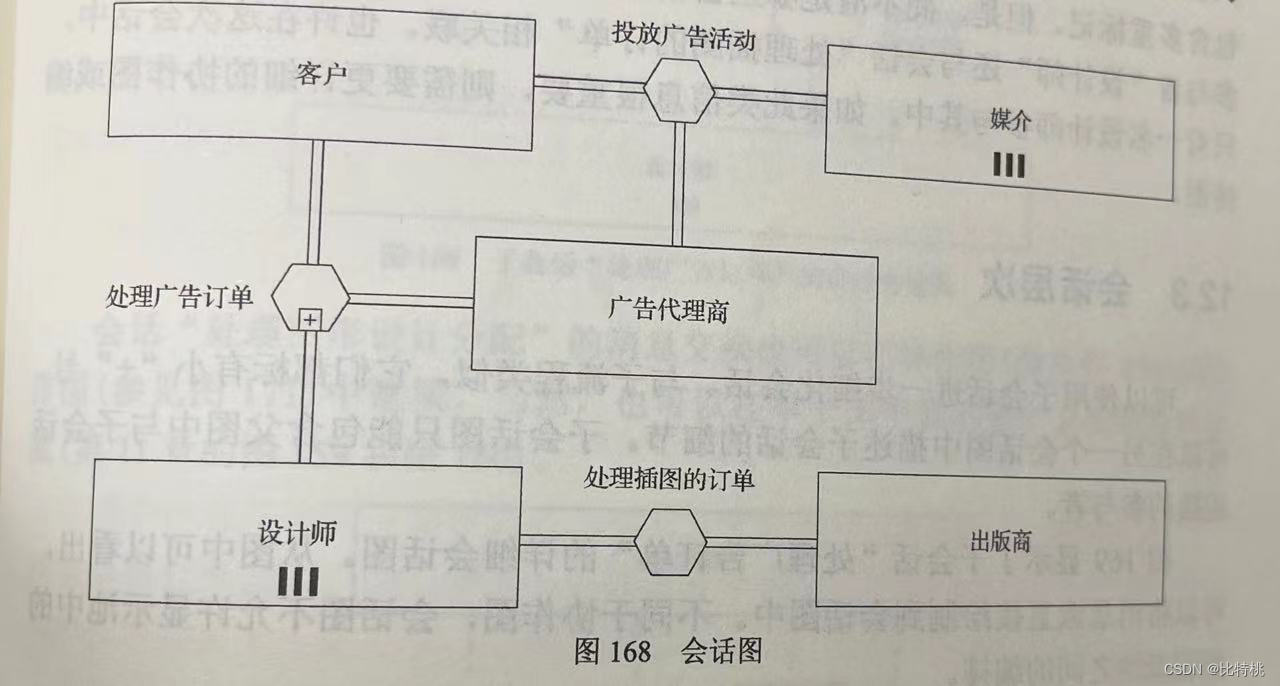
1.AVL平衡二叉树底层原理
-
背景
-
二叉查找树左右子树极度不平衡,退化成为链表时候,相当于全表扫描,时间复杂度就变为了O(n)
-
插入速度没影响,但是查询速度变慢,比单链表都慢,每次都要判断左右子树是否为空
-
需要保证二叉查找树一直保持平衡,就需要用到平衡二叉树
-

-
平衡二叉树
- 称为AVL树(Adelson-Velskii和Landis)平衡二叉查找树是一种特殊的二叉查找树每个节点的左右子树的高度差不能超过1。
- 平衡二叉树保证了树的构造是平衡的,当插入或删除数据导致不满足平衡二叉树不平衡时,会进行调整树上的节点来保持平衡。
-
平衡二叉树的插入和删除操作都是O(logn)的,因此它的查找性能很高,比非平衡的二叉查找树要快得多。
-
实现方式:红黑树、 Treap、伸展树等。
-
核心思想
-
在插入或删除节点时,如果发现子树不平衡,则对子树进行旋转操作,使其重新达到平衡
-
旋转操作有三种,哪边高度底就哪边旋转, 提升高度
- 左旋LL旋转
- 右旋RR旋转
- 左右LR双旋 和 右左RL双旋
-
-
图解过程




-
问题点
-
查找操作
- 二叉搜索树的时间复杂度介于O(log2N)到O(n)之间
- 如果退化成单链表,时间复杂度就是顺序查找,为O(n)
- 如果是平衡二叉树,查找效率会提高到O(log2N)
-
例子
- 平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。
- 假如磁盘每次寻道时间为10ms,在表数据量大时,查询性能就会很差
- 1百万的数据量,log2(N)约等于20次磁盘IO,时间20*10=0.2s
- log2(N) 相当于2的多少次方(立方)等于N,例:log2 (8)= 3
- 2的20次方=1048576,所以就是20次磁盘IO
-
不支持范围查询快速查找,范围查询时需要从根节点多次遍历,查询效率比较低
-
2.二叉树的演进之多叉树
-
背景
-
平衡二叉树操作效率高,但是存在不少问题,常规需要把树加载到内存里面
-
如果节点少则没问题,但是如果节点多 则高度很大,进行IO操作则存在性能问题
-
场景
- 平衡二叉树每个节点只存储一个键值和数据的,每个磁盘块仅仅存储一个键值和数据
- 如果要存储海量的数据,那构建平衡二叉树的时候耗时多
- 如果平衡二叉树的节点将会非常多,高度也会极其高,查找数据时会进行很多次磁盘 IO,效率将会极低
-
为了解决平衡二叉树的这个问题,设计一种单个节点可以存储多个键值和数据的平衡树,也就是我们接下来要说的 多叉树
-
-
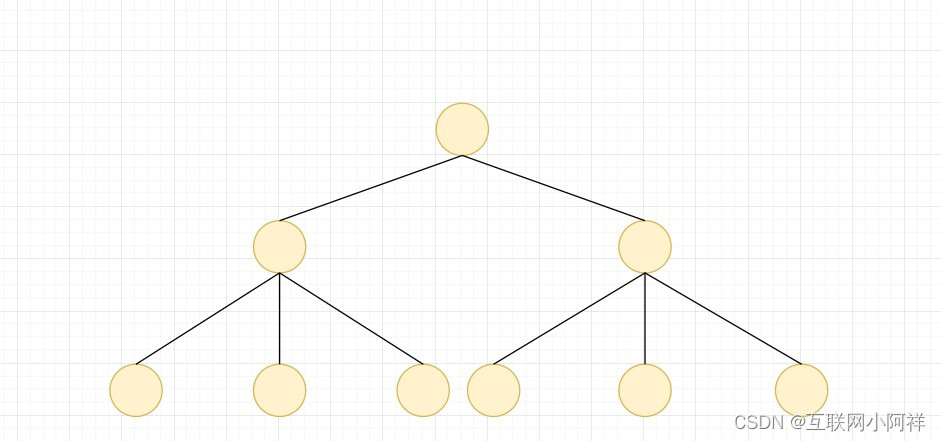
多叉树
-
也叫 多路查找树(muitl-way search tree)
-
每一个节点的子树可以多于两个,且每一个节点处可以存储多个元素,常见的就是B树、B+树等
- 注意:B是Balanced意思,不是Binary的意思
-
多叉树通过重新组织节点,降低了树的高度,可以提高IO效率
-
-
应用
-
操作系统IO操作都会利用磁盘预读原理,如果一个节点大小是一个存储页(4KB)
-
存储每个节点只需要一次IO即可完成存储
-
B树在存储系统里面广泛应用,比如数据库系统、文件系统等
都会利用磁盘预读原理,如果一个节点大小是一个存储页(4KB) -
存储每个节点只需要一次IO即可完成存储
-
B树在存储系统里面广泛应用,比如数据库系统、文件系统等
-
具体多叉树的应用及原理B-Tree和B+Tree的底层逻辑会在 MySQL底层存储B-Tree和B+Tree原理分析 中解释说明
-