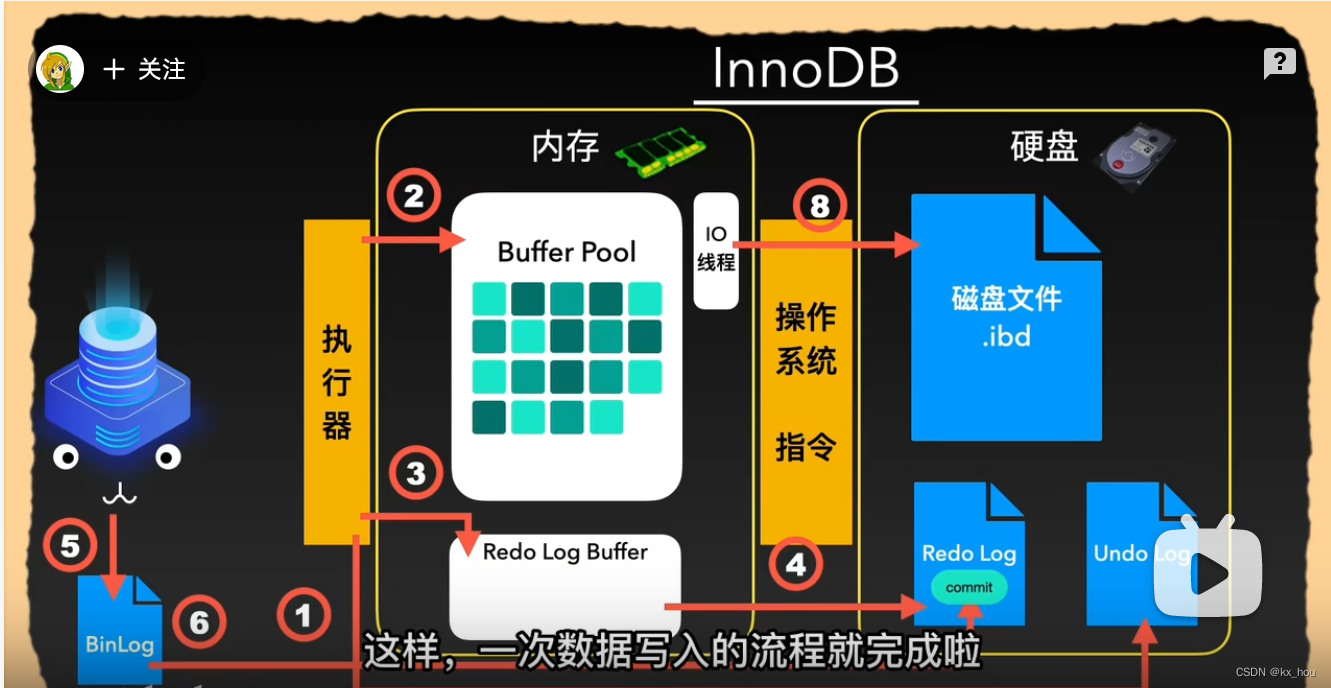
计算机底层：BDC码

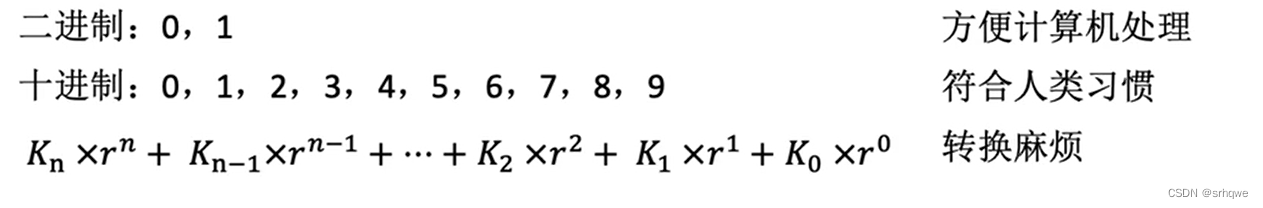
BDC码的作用：人类喜欢十进制，而机器适合二进制，因此当机器要翻译二进制给人看时，就会进行二进制和十进制的转换，而常规的转换法（k*位权）太麻烦。因此就出现了不同的转换方式，BCD码就可以方便地用二进制表示十进制。

BCD码的表示方式：将二进制的4个bit，作为一个十进制。这样就有2^4=16个的二进制状态，再规定这些状态，来表达十进制0-9的数字。因为0-9只需要10个的二进制状态，因此BCD码就会6种状态是冗余的。

冗余：没有用到，却可以用到的东西。

有了10中二进制状态就可以与0-9一一对应，以达到提高效率的作用

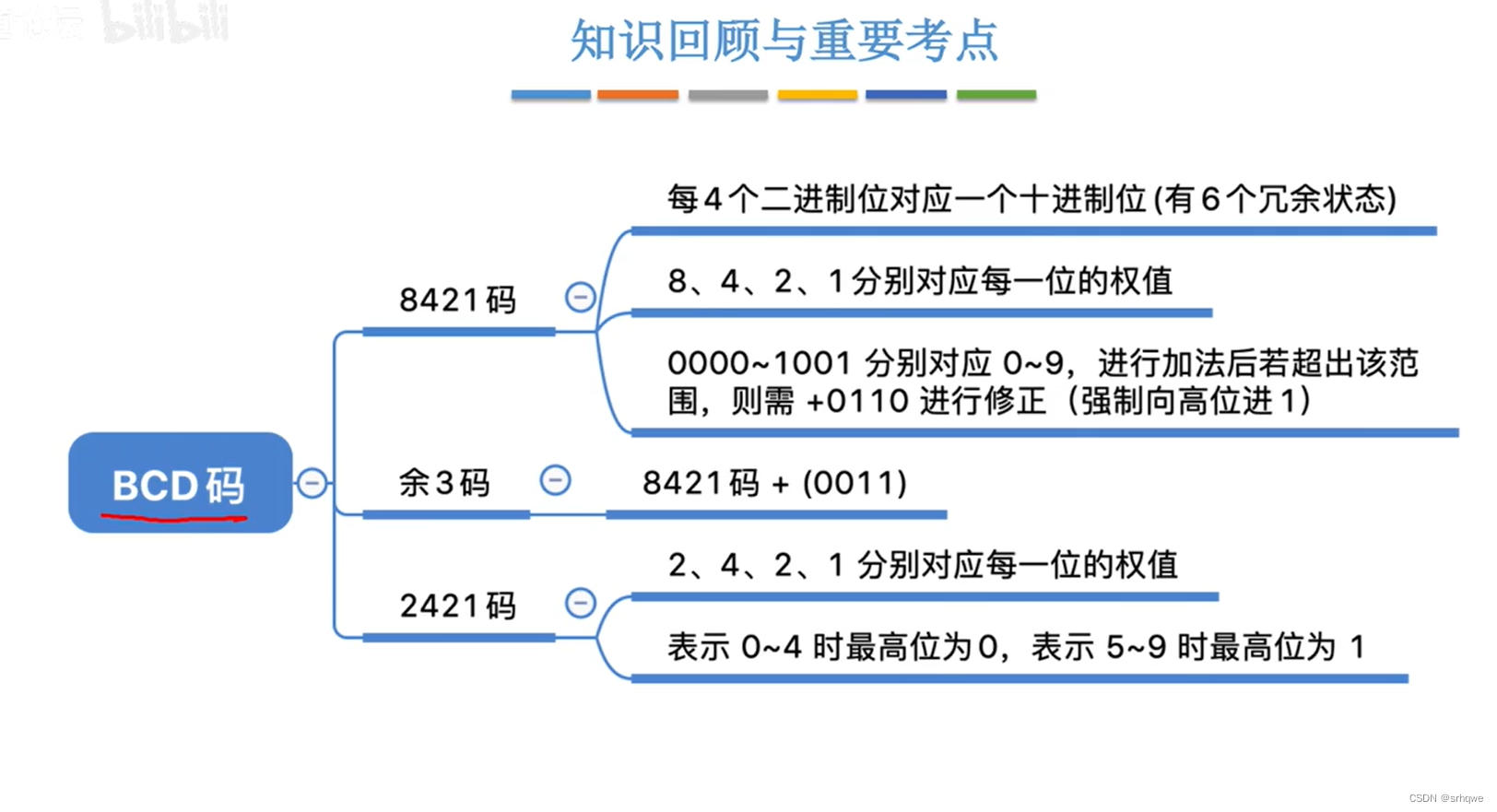
BCD码其中包括了： 8421码、余3码、2421码。

8421码：

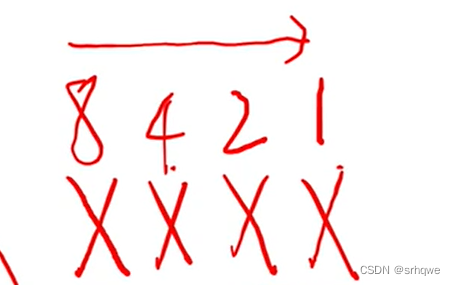
8421码表示的是：4个bit位的每位权重的8421,也就是2^3、2^2、2^1、2^0 。这是就是二进制转换十进制时的前四个位权。

这张图就是8421码对应0-9的数字。

如果表示985：

9：1001

8：1000

5：0101

结果就是，二进制：1001 1000 0101

十进制：985

8421码的运算：

先得出5+8=13得结果，然后拆开个位和十位，然后直接带入8421码。

最后得出：0001 0011

但是！这样并不是计算机底层的转换，这只是人工转换的一种技巧。比如做题的时候可以这样。但是计算机绝对不是这样！

计算机底层的转换：

计算机进行5+8，计算机会先将5和8分别对应8421码，转换成：0101、1000，再将这两串二进制丢给ALU计算逻辑单元，得出的结果就是：1101

但是会发现：1101并不在8421码规定的表中，也就是说1101在在8421码中没定义。

为了解决这一问题，8421码规定，如果超出得到1010-1111（8421码无定义）区间内的数，那么就会在无定义的这串二进制加上6，也就是加上0110。

因为8421码有定义的区间在0-9，10种二进制排序的可能；无定义的区间在10-15，5种二进制的可能，一共16种可能，（因为4个二进制可以表示16进制，你当成16进制看)无定义的数+6，超出了16，高位就会进1。

比如：13+6=19，其中大于16就会进1，得到13。

但计算机并不会看出13+6，而是看成8421码规定的二进制。也就是1101+0110=1 0011

最后在按照4个bit = 一个8421规定的十进制，最后可以拆开变成0001 0011

也就是:0001是1 ；0011是3，即：13

例子，9+9用8421码表示：

计算机从8421码表映射出来，变成1001+1001，计算机再把这些丢到ALU中，算出结果为：10010，计算机发现这串二进制在8421码的表中无法映射出结果，说明这串二进制在8421码中无定义，计算机就会将这串二进制+0110，也就是：10010+0110=11000，计算机+6得到一串二进制后，按照4bit拆开，0001 1000，再将每4个bit在8421表中映射，最终得到:18