引言
在cs224w课程中,我先后总结了deepwalk、node2vec,这两种算是最经典也是最主流的做法,而在 图节点嵌入相关算法学习笔记 中,从头至尾,将一些经典算法用wiki的数据集复现了一下,所以本篇博文,主要想提及一下之前有用到,但不是很懂原理的算法,不过这里就不会总结得跟之前的deepwalk、node2vec这么详细,只做个人理解并且能说明当前算法过程的总结。
LINE
LINE介绍
真实世界的信息网络中,能观察到的直接链接仅占很小的比例,大部分链接都因观察不到而缺失。比如社交网络中,很多线下的关系链并没有百分之百同步到线上。如果顶点 v v v 和 u u u 的链接发生缺失,则其一阶邻近度为
0,即使实际上它们关系非常密切。因此仅仅依靠一阶邻近度不足以描述网络的全局结构,我们需要寻找方法来解决这种因为大部分链接缺失导致的网络稀疏问题。
2014年的DeepWalk就是利用这种特征关系,采用了随机游走,来模拟这种二阶相似性,可它并没有提出相应的概率公式,LINE补充了这个方面,并一起提出了一阶相似性,如下图所示:
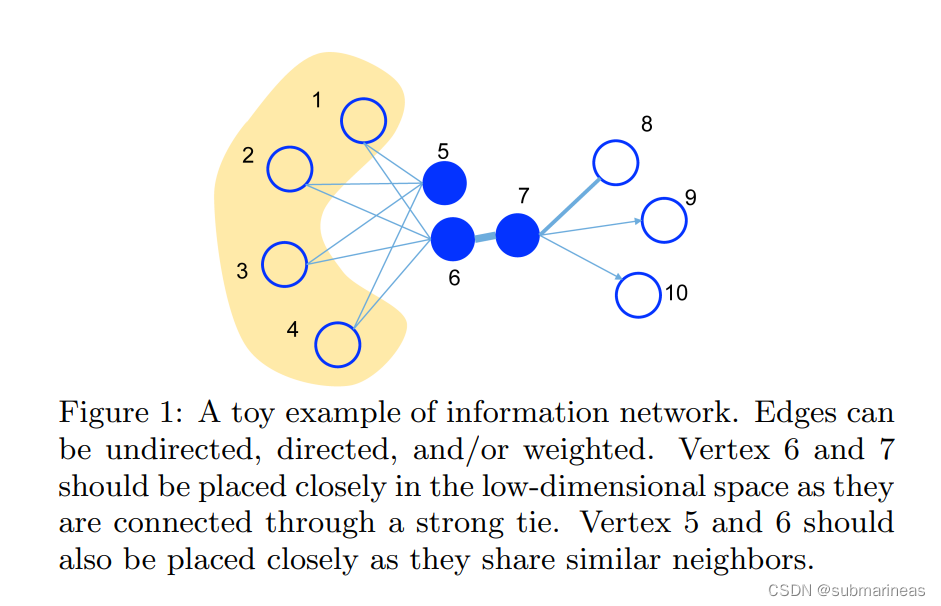
一阶相似性
网络中的一阶相似性是两个顶点之间的局部点对的相似度。对于有边
(
u
,
v
)
(u,v)
(u,v) 连接的每对顶点,该边的权重
W
u
v
W_{uv}
Wuv 表示
u
u
u和
v
v
v之间的一阶相似性,如果在
u
u
u和
v
v
v之间没有观察到边,他们的一阶相似性为0。
二阶相似度
二阶相似度表示节点邻域结构的相似性,它能够了表征全局的网络结构。数学上,让 p u = ( w u , 1 , . . . , w u , ∣ V ∣ ) p_{u} = (w_{u,1},...,w_{u,|V|}) pu=(wu,1,...,wu,∣V∣) 表示一阶附近 u u u与所有其他的顶点,那么 u u u和 v v v之间的二阶相似性由 p u p_{u} pu和 p v p_{v} pv之间的相似性来决定。即如果两个节点共享许多邻居,则它们趋于相似,如果没有一个顶点同时和 u u u和 v v v连接,那么二阶相似性是0.
这里举个例子,如上图所示:
- 顶点
6和7是直接相连,拥有较高的一阶相似度,因此相互之间关系密切。映射到低维空间时,这两个顶点的相似度应该较高。 - 顶点
6和5有相同的邻居结点,拥有较高的二阶相似度,因此关系也很密切。映射到低维空间时,这两个顶点的相似度也应该较高。
一般正常情况下,二阶相似度的点往往要比一阶多得多,这在下一节的SDNE论文中有根据arxiv−GrQc数据集中体现,如下图:

LINE 创新点
这里参考LINE:Large-scale Information Network Embedding阅读笔记
作为2015年的论文,LINE算法是作为对标deepwalk的,在deepwalk基础上补充的二阶相似度,以及提出了一阶相似度。
LINE模型的一阶相似性: 对每个无向边 ( i , j ) (i,j) (i,j),定义顶点 v i v_{i} vi 和 v j v_{j} vj 的概率联合分布公式为:
p 1 ( v i , v j ) = 1 1 + exp ( − u ⃗ i T ⋅ u ⃗ j ) p_{1}\left(v_{i}, v_{j}\right)=\frac{1}{1+\exp \left(-\vec{u}_{i}^{T} \cdot \vec{u}_{j}\right)} p1(vi,vj)=1+exp(−uiT⋅uj)1
其中 u ⃗ i ∈ R d \vec{u}_{i} \in R^{d} ui∈Rd 为顶点 v i v_{i} vi 的低维表达向量。
中间过程可以去看论文,大概就是为了在低维空间中保留一阶相似度,一个简单直接的方法是最小化目标函数,然后作者采用了 KL 散度作为两个分布的距离函数,因此最小化目标函数为:
O 1 = − ∑ ( i , j ) ∈ E w i , j × log p 1 ( v i , v j ) O_{1}=-\sum_{(i, j) \in E} w_{i, j} \times \log p_{1}\left(v_{i}, v_{j}\right) O1=−(i,j)∈E∑wi,j×logp1(vi,vj)
LINE模型的二阶相似性: 二阶相似性假定与其他顶点共享邻居顶点的两个点彼此相似(无向有向均可),一个向量 u u u和 u ′ u^{'} u′分别表示顶点本身和其他顶点的特定“上下文”,意为二阶相似。对于每个有向边 ( i , j ) (i,j) (i,j),我们首先定义由生成“上下文”的概率:
p 2 ( v j ∣ v i ) = exp ( u ⃗ j ′ T ⋅ u ⃗ i ) ∑ k = 1 ∣ V ∣ exp ( u ⃗ k ′ T ⋅ u ⃗ i ) p_{2}\left(v_{j} \mid v_{i}\right)=\frac{\exp \left(\vec{u}_{j}^{\prime T} \cdot \vec{u}_{i}\right)}{\sum_{k=1}^{|V|} \exp \left(\vec{u}_{k}^{\prime T} \cdot \vec{u}_{i}\right)} p2(vj∣vi)=∑k=1∣V∣exp(uk′T⋅ui)exp(uj′T⋅ui)
这个公式在node2vec论文中也被提及了,不过是作为特征空间对称性假设进行推导,这里的推导还是以优化最小化一个目标函数:
O 2 = ∑ i ∈ V λ i d ( p ^ 2 ( ⋅ ∣ v i ) , p 2 ( ⋅ ∣ v i ) ) O_{2}=\sum_{i \in V} \lambda_{i} d\left(\hat{p}_{2}\left(\cdot \mid v_{i}\right), p_{2}\left(\cdot \mid v_{i}\right)\right) O2=i∈V∑λid(p^2(⋅∣vi),p2(⋅∣vi))
其中 d ( , ) d(,) d(,)为两种分布之间的距离, λ i \lambda_{i} λi来表示网络中顶点 i i i的声望,然后考虑计算资源问题,所以这里就提出了负采样策略,即:
J p o s ( u , v ) = − log ( σ ( s ( f ( u ) , f ( v ) ) ) ) − ∑ i = 1 K E v n P n ( v ) [ log ( σ ( − s ( f ( u ) , f ( v n ) ) ) ) ] J_{pos}(u, v) = -\log(\sigma(s(f(u), f(v)))) - \sum_{i=1}^{K} E_{v_n ~ P_n(v)} [\log(\sigma(-s(f(u), f(v_n))))] Jpos(u,v)=−log(σ(s(f(u),f(v))))−i=1∑KEvn Pn(v)[log(σ(−s(f(u),f(vn))))]
而上述函数又可通过采用异步随机梯度下降算法(ASGD)来优化。每一步中,ASGD算法对小批量边缘进行抽样,然后更新模型参数。但是这也带来一个问题,如果我们根据小权重的边缘选择较大的学习率,那么大权重的边上的梯度就会爆炸式的过大,如果我们根据具有较大权重的边选择学习小的速率,那么小权重上的边的梯度将变得太小。因此边缘采样同样要优化。从起始边缘采样并将采样的边缘作为二进制边缘,其中采样概率与原始边缘的权重成比例。
这里可以对比我之前的node2vec笔记一起看,代码复现的话可以参照图节点嵌入相关算法学习笔记 中,使用wiki数据集,用浅梦大佬的ge包进行了测试。
LINE优缺点
优点:
- 基于deepwalk,保留节点之间的一阶相似性(first-order proximity)和二阶相似性(second-order proximity)
- 可以处理上亿级别的大规模网络(论文中后续有所证明)
- 采用负采样的方式对模型进行优化,以及利用 Alias table加速采样过程。(我之前一直以为node2vec先用来着,原来还早一年)
缺点:
- 它不能处理动态变化的网络,因为需要重新计算所有顶点的嵌入。
- 不能很好处理多阶相似度,或者说高阶相似度,不能捕获到。
- 需要大量的内存和计算资源
另外我参考的知乎贴的评论中,有一个大佬对LINE算法提出了很多质疑,并提出了LINE的一阶和二阶相似性都是等价于矩阵分解的,具体证明参照论文:https://arxiv.org/pdf/1707.05926.pdf
这里Mark一下,之后有时间回头看看。
SDNE
SDNE介绍
虽然上节中LINE解决了deepwalk中的很多问题,但是它依然是一个基于浅层模型网络 embedding 的方法,由于浅层模型的表达能力有限,所以这些方法很难捕获高度非线性的网络结构,因此得到的是次优(非最优)的网络 representation
当然,还有几个亘古不变的问题,论文中又把deepwalk中提到的几个难点复述了一下,即 non-linear,structure-preserving,sparsity。但这波算是解决了non-linear,其它还是沿用LINE,做了一些创新。
SDNE(Structural Deep Network Embedding )是和node2vec并列的工作,均发表在2016年的KDD会议中。可以看作是基于LINE的扩展,同时也是第一个将深度学习应用于网络表示学习中的方法。 它使用一个自动编码器结构来同时优化1阶和2阶相似度(LINE是分别优化的),学习得到的向量表示能够保留局部和全局结构,并且对稀疏网络具有鲁棒性。
创新点
SDNE模型采用多层神经网络将输入数据映射到高度非线性的潜在空间来捕获高度非线性的网络结构,模型结构如下图:
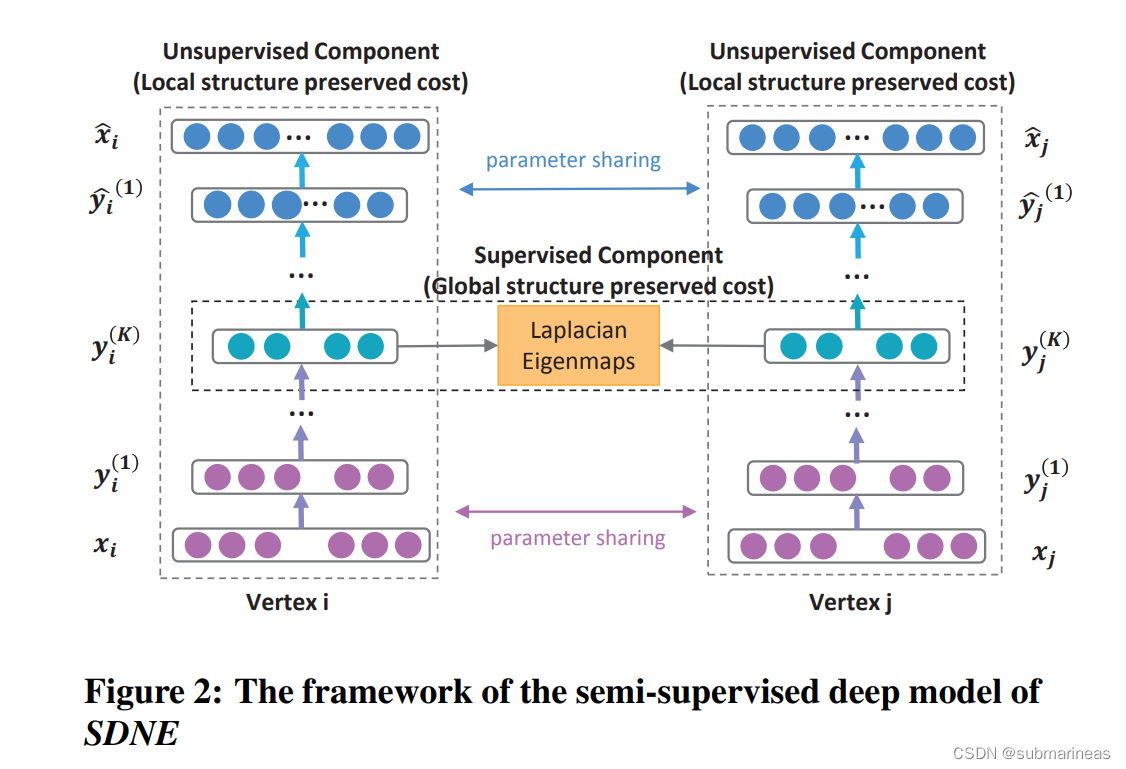
其中,从
x
i
x_{i}
xi 到
y
i
(
K
)
y_{i}^{(K)}
yi(K)是编码器,从
y
i
(
K
)
y_{i}^{(K)}
yi(K) 到
x
^
i
\hat{x}_{i}
x^i是解码器,
y
i
(
K
)
y_{i}^{(K)}
yi(K)是节点
i
i
i 的embedding向量,SDNE是基于给定图转化的邻接矩阵和深度自编码器来保留二阶相似度。编码器的公式为:
y i ( 1 ) = σ ( W ( 1 ) x i + b ( 1 ) ) y i ( k ) = σ ( W ( k ) y i ( k − 1 ) + b ( k ) ) , k = 2 , … , K \begin{array}{c} y_{i}^{(1)}=\sigma\left(W^{(1)} x_{i}+b^{(1)}\right) \\ \\ y_{i}^{(k)}=\sigma\left(W^{(k)} y_{i}^{(k-1)}+b^{(k)}\right), k=2, \ldots, K \end{array} yi(1)=σ(W(1)xi+b(1))yi(k)=σ(W(k)yi(k−1)+b(k)),k=2,…,K
其中, σ ( . . . ) \sigma(...) σ(...) 为非线性激活函数, { W ( k ) , b ( k ) } k = 1 , ⋯ , K \left\{\mathbf{W}^{(k)}, {\mathbf{b}}^{(k)}\right\}_{k=1, \cdots, K} {W(k),b(k)}k=1,⋯,K 为编码器参数。
假设假设解码器为 K + 1 K+1 K+1 层,则解码过程为:
y → ^ i ( K ) = σ ( W ^ ( K ) y → i ( K ) + b → ^ ( K ) ) y → ^ i ( K − 1 ) = σ ( W ^ ( K − 1 ) y → ^ i ( K ) + b → ^ ( K − 1 ) ) . . . y → ^ i ( 1 ) = σ ( W ^ ( 1 ) y → ^ i ( 2 ) + b → ^ ( 1 ) ) x → ^ i = σ ( W ^ ( 0 ) y → ^ i ( 1 ) + b → ^ ( 0 ) ) \begin{array}{l} \hat{\overrightarrow{\mathbf{y}}}_{i}^{(K)}=\sigma\left(\hat{\mathbf{W}}^{(K)} \overrightarrow{\mathbf{y}}_{i}^{(K)}+\hat{\overrightarrow{\mathbf{b}}}^{(K)}\right) \\ \hat{\overrightarrow{\mathbf{y}}}_{i}^{(K-1)}=\sigma\left(\hat{\mathbf{W}}^{(K-1)} \hat{\overrightarrow{\mathbf{y}}}_{i}^{(K)}+\hat{\overrightarrow{\mathbf{b}}}^{(K-1)}\right) \\ ... \\ \hat{\overrightarrow{\mathbf{y}}}_{i}^{(1)}=\sigma\left(\hat{\mathbf{W}}^{(1)} \hat{\overrightarrow{\mathbf{y}}}_{i}^{(2)}+\hat{\overrightarrow{\mathbf{b}}}^{(1)}\right) \\ \hat{\overrightarrow{\mathbf{x}}}_{i}=\sigma\left(\hat{\mathbf{W}}^{(0)} \hat{\overrightarrow{\mathbf{y}}}_{i}^{(1)}+\hat{\overrightarrow{\mathbf{b}}}^{(0)}\right) \\ \end{array} y^i(K)=σ(W^(K)yi(K)+b^(K))y^i(K−1)=σ(W^(K−1)y^i(K)+b^(K−1))...y^i(1)=σ(W^(1)y^i(2)+b^(1))x^i=σ(W^(0)y^i(1)+b^(0))
其中,上述的参数变为了与编码器相反的解码器参数。
所以最终自编码器的损失函数为:
L 2 n d = ∑ i = 1 n ∥ x ^ i − x i ∥ 2 2 L_{2 n d}=\sum_{i=1}^{n}\left\|\hat{x}_{i}-x_{i}\right\|_{2}^{2} L2nd=i=1∑n∥x^i−xi∥22
但由于图的稀疏性,往往非零元素远远少于零元素的数量的,而如果直接输入到神经网络中,结果也会更加离散,倾向于0这也是一个不错的结果,所以作者这里提出了一个带权损失函数,即给非零元素赋予比零元素更大的误差,为:
L 2 n d = ∑ i = 1 n ∥ ( x ^ i − x i ) ⊙ b i ∥ 2 2 = ∥ ( X ^ − X ) ⊙ B ∥ F 2 L_{2 n d}=\sum_{i=1}^{n}\left\|\left(\hat{x}_{i}-x_{i}\right) \odot \mathbf{b}_{\mathbf{i}}\right\|_{2}^{2}=\|(\hat{X}-X) \odot B\|_{F}^{2} L2nd=i=1∑n∥(x^i−xi)⊙bi∥22=∥(X^−X)⊙B∥F2
其中
⊙
\odot
⊙ 为Hadamard(逐元素积),
b
i
b_{i}
bi 为:
b i , j = { 1 , if x i , j = 0 β , else b_{i, j}=\left\{\begin{array}{ll} 1, & \text { if } x_{i, j}=0 \\ \beta, & \text { else } \end{array}\right. bi,j={1,β, if xi,j=0 else
即:
- 若顶点 v i v_{i} vi , v j v_{j} vj 存在链接( S i , j ≠ 0 S_{i,j}\ne 0 Si,j=0),则误差权重为 β \beta β,其中 β > 1 \beta > 1 β>1 为超参数。
- 若顶点 v i v_{i} vi , v j v_{j} vj 不存在链接 ( S i , j = 0 S_{i,j} = 0 Si,j=0),则误差权重为1
这是无监督的部分,通过自编码器保存了网络的全局结构,而有监督的部分则是保留网络的局部结构,因为一阶相似度可以表示网络的局部结构。
用一个拉普拉斯特征映射捕获一阶相似度(上述框架图中中间横向部分),若顶点 v i v_{i} vi , v j v_{j} vj 之间存在边,那他们的Embedding的结果 y ( K ) y^{(K)} y(K) 也接近,则直接给出损失函数为:
L 1 s t = ∑ i , j = 1 n s i , j ∥ y i ( K ) − y j ( K ) ∥ 2 2 = ∑ i , j = 1 n s i , j ∥ y i − y j ∥ 2 2 L_{1 s t}=\sum_{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{\mathbf{i}}{ }^{(K)}-\mathbf{y}_{\mathbf{j}}{ }^{(K)}\right\|_{2}^{2}=\sum_{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{\mathbf{i}}-\mathbf{y}_{\mathbf{j}}\right\|_{2}^{2} L1st=i,j=1∑nsi,j yi(K)−yj(K) 22=i,j=1∑nsi,j∥yi−yj∥22
该损失函数参考了Laplacian Eigenmaps思想,所以论文后又写成了:
L 1 s t = ∑ i , j = 1 n ∥ y i − y j ∥ 2 2 = 2 tr ( Y T L Y ) L_{1 s t}=\sum_{i, j=1}^{n}\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|_{2}^{2}=2 \operatorname{tr}\left(Y^{T} L Y\right) L1st=i,j=1∑n∥yi−yj∥22=2tr(YTLY)
其中 L L L是图对应的拉普拉斯矩阵,S是邻接矩阵,关于这个公式的具体说明我去找了篇论文,即:
Laplacian Eigenmaps from Sparse, Noisy Similarity
Measurements (https://arxiv.org/pdf/1603.03972v2.pdf)
总结就是Laplacian Eigenmaps是一种图嵌入方法,它利用图的拉普拉斯算子的特征值和特征向量来得到数据点的低维表示。
最后,为同时保留一阶邻近度和二阶邻近度,SDNE 提出了一个半监督学习模型,其目标函数为:
L m i x = L 2 n d + α L 1 s t + ν L r e g L_{m i x}=L_{2 n d}+\alpha L_{1 s t}+\nu L_{r e g} Lmix=L2nd+αL1st+νLreg
其中, L r e g L_{reg} Lreg 是正则化项, α \alpha α为控制1阶损失的参数 , v v v为控制正则化项的参数。
复现SDNE算法的demo可以见:
https://github.com/CyrilZhao-sudo/SDNE
因为浅梦大佬的SDNE用的tensorflow版本实在太低,目前基本已经无法再跑了,如果不降级。
这里我引出论文中一张tsne降维图,感觉很不错:

SDNE算法的优缺点
关于这个,其实我在看论文和找下论文笔记的时候,相对LINE和node2vec,优缺点都是很明显的,因为算line的更进一步。
优点:
- 它是第一个将深度学习应用于图嵌入的方法,可以利用神经网络的强大表达能力来学习高度非线性的网络结构。
- 它可以同时优化一阶邻近度和二阶邻近度,捕捉图的局部和全局结构,同时保持节点嵌入的稀疏性和平滑性。
- 它同LINE一样,可以处理大规模的图数据,因为使用了梯度下降。
缺点:
- 它需要调整很多超参数,比如隐藏层的数量、大小、激活函数等,这些参数会影响模型的效果和效率。
- 它不能处理动态变化的图数据,因为它是基于批量训练的方法,如果图结构发生变化,就需要重新训练模型。
- 它不能处理带有节点属性或者边权重的图数据,因为它只考虑了节点之间是否存在边,而没有考虑边或者节点本身的信息。
struc2vec
struc2vec介绍
在stuc2vec之前的图嵌入算法,如DeepWalk、LINE、SDNE等,都是基于近邻相似假设的,即认为图中相邻或者接近的节点具有相似的特征或者属性。其中DeepWalk,Node2Vec通过随机游走在图中采样顶点序列来构造顶点的近邻集合。LINE显式的构造邻接点对和顶点的距离为1的近邻集合。SDNE使用邻接矩阵描述顶点的近邻结构。
然而,在一些应用场景中,我们更关心节点的结构相似性,即节点在图中所处的拓扑位置和角色是否相似,而不是它们是否直接连接或者共享邻居。
比如说 几种常见的Graph Embedding方法 提到在蚂蚁金服风控模型使用struc2vec相比node2vec有质的提升,这是因为在风控领域,你可信并不能代表你的邻居可信(有些“大 V”节点的邻居众多),但是一个直观的感觉是,如果两个人在图中处于相似的地位(比如两个“大 V”),那么这两个人应该都可信或都不可信,并且一般来说这样两个人(节点)相距较远。
论文中引用的图与例子为:
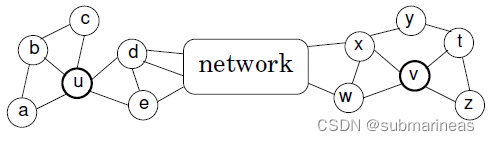
其中
v
v
v 和
u
u
u 顶点扮演相似的角色(具有相似的局部结构),但是它们在网络上相距甚远。由于它们的邻域不相交,似乎之前的算法就无法很好的捕获它们的结构相似性,文中提到的是structural equivalence,所以,论文《struc2vec: Learning Node Representations from Structural Identity》提出了一个学习结构等效性的无监督学习框架——struc2vec。
struc2vec创新点
本节也不算创新点,因为整个算法都不走之前的路了,直接提出了很多全新的概念。整体来讲,说复杂也不复杂,但说简单很多细节又需要很多前置条件,我这里简单讲下我觉得比较有意思的点,之后有时间把整篇再过一遍。
Dynamic Time Warping(DTW)
首先,为了表示结构相似性,论文直接就开始定义了一些符号:
-
R k ( u ) R_{k}(u) Rk(u)表示了节点 u u u的 k k k级邻域。
-
s ( S ) s(S) s(S) 则表示节点的集合 S ⊂ V S⊂V S⊂V 的度数序列。
-
g ( D 1 , D 2 ) g(D_{1},D_{2}) g(D1,D2)度量了两个度数序列D1,D2之间的距离
-
f k ( u , v ) f_{k}(u,v) fk(u,v)表示了u,v两节点之间,k级邻域(距离小于等于k的节点和所有它们之间的边)的结构距离。
然后直接给出公式衡量节点 u u u 和 v v v 之间的相似度:
f k ( u , v ) = f k − 1 ( u , v ) + g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) , k ≥ 0 and ∣ R k ( u ) ∣ , ∣ R k ( v ) ∣ > 0 f_{k}(u, v)=f_{k-1}(u, v)+g\left(s\left(R_{k}(u)\right), s\left(R_{k}(v)\right)\right), k \geq 0 \text { and }\left|R_{k}(u)\right|,\left|R_{k}(v)\right|>0 fk(u,v)=fk−1(u,v)+g(s(Rk(u)),s(Rk(v))),k≥0 and ∣Rk(u)∣,∣Rk(v)∣>0
这是一个递归式,可以认为 f k ( u , v ) f_{k}(u,v) fk(u,v) 值越小,则节点 u u u 和 v v v 结构相似度越高。
而这里的 g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) g\left(s\left(R_{k}(u)\right), s\left(R_{k}(v)\right)\right) g(s(Rk(u)),s(Rk(v))) 的计算,其实就是用的DTW算法。
关于DTW算法,从我个人理解角度来看,整体其实就是动态规划,只不过动态规划是一种解决最优化的通用算法,而DTW算法是一种利用动态规划算法来计算两个时序列之间相似度的方法。具体的我们来复习一波动态转移方程,公式为:
d p [ i ] [ j ] = grid [ i ] [ j ] + { min ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) ( i > 0 , j > 0 ) d p [ i − 1 ] [ j ] ( i > 0 , j = 0 ) d p [ i ] [ j − 1 ] ( i > 0 , j > 0 ) 0 ( i = 0 , j = 0 ) d p[i][j]=\operatorname{grid}[i][j]+\left\{\begin{array}{c} \min (d p[i-1][j], d p[i][j-1]) \quad(i>0, j>0) \\ d p[i-1][j] \quad(i>0, j=0) \\ d p[i][j-1] \quad(i>0, j>0) \\ 0 \quad(i=0, j=0) \end{array}\right. dp[i][j]=grid[i][j]+⎩ ⎨ ⎧min(dp[i−1][j],dp[i][j−1])(i>0,j>0)dp[i−1][j](i>0,j=0)dp[i][j−1](i>0,j>0)0(i=0,j=0)
具体的可以看一道例题,因为我也LeetCode很久没刷了,这里找回一下,在LeetCode中比较经典的剑指 Offer 12. 矩阵中的路径
给定一个包含非负整数的
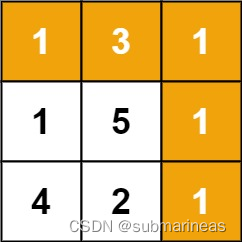
m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明: 一个机器人每次只能向下或者向右移动一步。
其中,输入:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
该题就是一道很标准的动态规划示例题,根据LeetCode中的明了分析过程 简单dp 矩阵的最小路径和 题解:
-
问题: 从左上角到左下角的最小路径和。子问题:从左上角到任意位置的最小路径和。
-
状态定义: f ( i , j ) f(i,j) f(i,j) 是从左上角 ( 0 , 0 ) (0,0) (0,0) 到当前位置 ( i , j ) (i,j) (i,j) 的最小路径和。
-
转移方程: 左一位置和上一位置的最短路径和的最小值,再加上当前位置的值,就是当前位置的最短路径和。
f ( i , j ) = min { f ( i − 1 , j ) , f ( i , j − 1 ) } + arr [ i ] [ j ] f(i, j)=\min \{f(i-1, j), f(i, j-1)\}+\operatorname{arr}[i][j] f(i,j)=min{f(i−1,j),f(i,j−1)}+arr[i][j] -
初始值:最左一列和第一行的所有位置都必须作为初始值,防止转移方程越界。
f ( 0 , j ) = f ( 0 , j − 1 ) + arr [ 0 ] [ j ] f ( i , 0 ) = f ( i − 1 , 0 ) + arr [ i ] [ 0 ] \begin{aligned} f(0, j) & =f(0, j-1)+\operatorname{arr}[0][j] \\ \\ f(i, 0) & =f(i-1,0)+\operatorname{arr}[i][0] \end{aligned} f(0,j)f(i,0)=f(0,j−1)+arr[0][j]=f(i−1,0)+arr[i][0] -
返回值:返回数组右下角的值 f ( m − 1 , n − 1 ) f(m-1,n-1) f(m−1,n−1)
则python的代码为:
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
if not grid or not grid[0]:
return 0
rows, columns = len(grid), len(grid[0])
dp = [[0] * columns for _ in range(rows)]
dp[0][0] = grid[0][0]
for i in range(1, rows):
dp[i][0] = dp[i - 1][0] + grid[i][0]
for j in range(1, columns):
dp[0][j] = dp[0][j - 1] + grid[0][j]
for i in range(1, rows):
for j in range(1, columns):
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
return dp[rows - 1][columns - 1]
而DTW只不过是还多了一种状态,递推公式为:
L min ( i , j ) = min { L min ( i , j − 1 ) , L min ( i − 1 , j ) , L min ( i − 1 , j − 1 ) } + M ( i , j ) L_{\min }(i, j)=\min \left\{L_{\min }(i, j-1), L_{\min }(i-1, j), L_{\min }(i-1, j-1)\right\}+M(i, j) Lmin(i,j)=min{Lmin(i,j−1),Lmin(i−1,j),Lmin(i−1,j−1)}+M(i,j)
具体的以及例子可以看如下两篇:
动态时间规整(DTW)算法简介 (例子和图很形象)
动态时间规整-DTW算法(该算法的提出到原理都很清晰,带python代码)
以上总结一句话,DTW可以用来衡量两个不同长度且含有重复元素的的序列的距离(距离的定义可以自己设置)。
文章基于此提出一种压缩表示方法,对于序列中出现的每一个度,计算该度在序列里出现的次数。压缩后的有序度序列存储的是(度数,出现次数)这样的二元组。具体计算公式为:
dist ( a , b ) = ( max ( a 0 , b 0 ) min ( a 0 , b 0 ) − 1 ) max ( a 1 , b 1 ) \operatorname{dist}(\boldsymbol{a}, \boldsymbol{b})=\left(\frac{\max \left(a_{0}, b_{0}\right)}{\min \left(a_{0}, b_{0}\right)}-1\right) \max \left(a_{1}, b_{1}\right) dist(a,b)=(min(a0,b0)max(a0,b0)−1)max(a1,b1)
其中 a = ( a 0 , a 1 ) and b = ( b 0 , b 1 ) 是作为元组 in A ′ and B ′ \boldsymbol{a}=\left(a_{0}, a_{1}\right) \text { and } \boldsymbol{b}=\left(b_{0}, b_{1}\right) \text { 是作为元组 in } A^{\prime} \text { and } B^{\prime} a=(a0,a1) and b=(b0,b1) 是作为元组 in A′ and B′, A ′ and B ′ A^{\prime} \text { and } B^{\prime} A′ and B′ 是压缩之后的元组序列
biased random walk
利用 M M M 生成节点的上下文的过程:带偏的随机游走(biased random walk)。
- 每次采样时,首先决定是在当前层游走,还是切换到上下层的层游走。
- 若决定在当前层游走,设当前处于第k层,则从顶点 u u u 到顶点 v v v 的概率为:
p k ( u , v ) = e − f k ( u , v ) Z k ( u ) p_{k}(u, v)=\frac{e^{-f_{k}(u, v)}}{Z_{k}(u)} pk(u,v)=Zk(u)e−fk(u,v)
其中 p k ( u , v ) = e − f k ( u , v ) Z k ( u ) Z k ( u ) = ∑ v ∈ V , v ≠ u e − f k ( u , v ) p_{k}(u, v)=\frac{e^{-f_{k}(u, v)}}{Z_{k}(u)}Z_{k}(u)=\sum_{v \in V, v \neq u} e^{-f_{k}(u, v)} pk(u,v)=Zk(u)e−fk(u,v)Zk(u)=∑v∈V,v=ue−fk(u,v) 是第k层中关于顶点u的归一化因子。
通过在图M中进行随机游走,每次采样的顶点更倾向于选择与当前顶点结构相似的顶点。因此,采样生成的上下文顶点很可能是结构相似的顶点,这与顶点在图中的位置无关。
若决定切换不同的层,假设在往上( k − 1 k - 1 k−1)层概率上 1 − q 1-q 1−q,则换到 k + 1 k+1 k+1 层的概率为:
p k ( u k , u k + 1 ) = w ( u k , u k + 1 ) ( u k , u k + 1 ) + ( u k , u k − 1 ) p_k(u_k, u_{k+1}) = \frac{w(u_k, u_{k+1})}{(u_k, u_{k+1})+(u_k, u_{k-1})} pk(uk,uk+1)=(uk,uk+1)+(uk,uk−1)w(uk,uk+1)
而换到 k − 1 k−1 k−1 层的概率为:
p k ( u k , u k − 1 ) = 1 − p k ( u k , u k + 1 ) p_k(u_k, u_{k-1}) = 1 - p_k(u_k, u_{k+1}) pk(uk,uk−1)=1−pk(uk,uk+1)
Constructing the context graph
根据上一节的DTW距离定义,对于每一个 k k k 我们都可以计算出两个顶点之间的一个距离,现在要做的是通过上一节得到的顶点之间的有序度序列距离来构建一个层次化的带权图(用于后续的随机游走)。
我们定义在某一层k中两个顶点的边权为 w k ( u , v ) = e − f k ( u , v ) , k = 0 , … , k ∗ w_{k}(u, v)=e^{-f_{k}(u, v)}, k=0, \ldots, k^{*} wk(u,v)=e−fk(u,v),k=0,…,k∗
因为 f k ( u , v ) f_k(u,v) fk(u,v) 最小是0,那么边的权重 w k ( u , v ) w_{k}(u,v) wk(u,v) 的取值范围是 ( 0 , 1 ] (0,1] (0,1] ,当等于1时,代表两个节点结构相同。
通过有向边将属于不同层次的同一顶点连接起来,具体来说,对每个顶点,都会和其对应的上层顶点( k − 1 k-1 k−1层)还有下层顶点( k + 1 k+1 k+1层)相连。边权定义为:
w ( u k , u k + 1 ) = l o g ( Γ k ( u ) + e ) , k = 0 , … , k ∗ − 1 w(u_k,u_{k+1})=log(\Gamma_k(u)+e), k=0,…,k^∗−1 w(uk,uk+1)=log(Γk(u)+e),k=0,…,k∗−1
w ( u k , u k − 1 ) = 1 , k = 1 , … , k ∗ w(u_k,u_{k-1})=1,k=1,…,k^∗ w(uk,uk−1)=1,k=1,…,k∗
其中 Γ k ( u ) \Gamma_k(u) Γk(u) 代表了指向节点 u u u 的权重大于 k k k 层图平均权重的边的数量:
Γ k ( u ) = ∑ v ∈ V 1 ( w k ( u , v ) > w k ‾ ) \Gamma_k(u)=\sum_{v \in V} \mathbb{1}(w_k(u,v) > \overline{w_k}) Γk(u)=v∈V∑1(wk(u,v)>wk)
struc2vec的优缺点
优点:
- 它可以有效地区分不同层次的结构相似性,例如角色相似性和社区相似性
- 它可以利用现有的序列嵌入方法,如word2vec,来学习节点的向量表示
缺点:
- 它需要计算图中所有节点对之间的结构距离,这可能会导致较高的时间和空间复杂度
- 它需要设置一些超参数,如随机游走长度、步数、窗口大小等,这可能会影响嵌入结果
关于上述三个点,在我参考中的浅梦大佬已经对这些进行了复现,写得十分形象了,比如说我上面感兴趣的DTW,这里代码为:
def compute_dtw_dist(part_list, degreeList, dist_func):
dtw_dist = {}
for v1, nbs in part_list:
lists_v1 = degreeList[v1] # lists_v1 :orderd degree list of v1
for v2 in nbs:
lists_v2 = degreeList[v2] # lists_v1 :orderd degree list of v2
max_layer = min(len(lists_v1), len(lists_v2)) # valid layer
dtw_dist[v1, v2] = {}
for layer in range(0, max_layer):
dist, path = fastdtw(
lists_v1[layer], lists_v2[layer], radius=1, dist=dist_func)
dtw_dist[v1, v2][layer] = dist
return dtw_dist
def _compute_structural_distance(self, max_num_layers, workers=1, verbose=0,):
pass
因为DTW在python中是有一个包的,就叫fastdtw,那就能直接
s
(
R
k
(
u
)
)
s(R_{k}(u))
s(Rk(u)),然后接着计算顶点对之间的距离。具体见参考链接。
另外,本篇中只是引出了三种比较主流的算法(因为github复现的多,emmm),另外的如下图所示,感兴趣的可以再继续研究,当然先排除graphGAN,在我上一篇图嵌入算法实践中,发现这是个无法复现的算法,如果想究其原因,去看看issue上各种比deepwalk还低的embed分数就知道了。
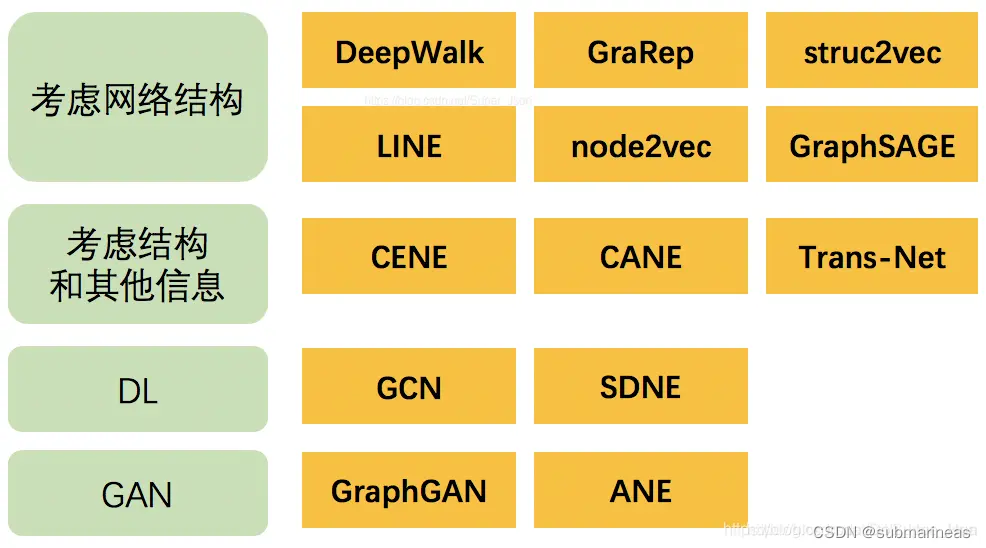
参考与推荐
https://arxiv.org/pdf/1503.03578.pdf
[1]. LINE: Large-scale Information Network Embedding
[2]. Structural Deep Network Embedding
[3]. struc2vec: Learning Node Representations from Structural
Identity
[4]. Laplacian Eigenmaps from Sparse, Noisy Similarity
Measurements
[5]. https://www.huaxiaozhuan.com/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/chapters
[6]. 【Graph Embedding】Struc2Vec:算法原理,实现和应用
[7]. Deep Learning on Graphs: A Survey