题目链接

leetcode在线oj题——N皇后

题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

题目示例

示例1:
在这里插入图片描述
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例2:
输入：n = 1
输出：[[“Q”]]

题目提示

1 <= n <= 9

解题思路

使用深度搜索的方法，按照先行后列的顺序，查看每一个位置是否满足条件

先从第一行第一列开始，使这个位置占一个皇后，显然第一行和第一列，与其所在斜线都无法再放皇后了
在这里插入图片描述
然后按照顺序将第二个皇后放在第二行第三列
显然这种放法只能支持三个皇后

那么回退到上一个状态（第一个皇后在第一行第一列），按照顺序将第二个皇后放在第二行第四列

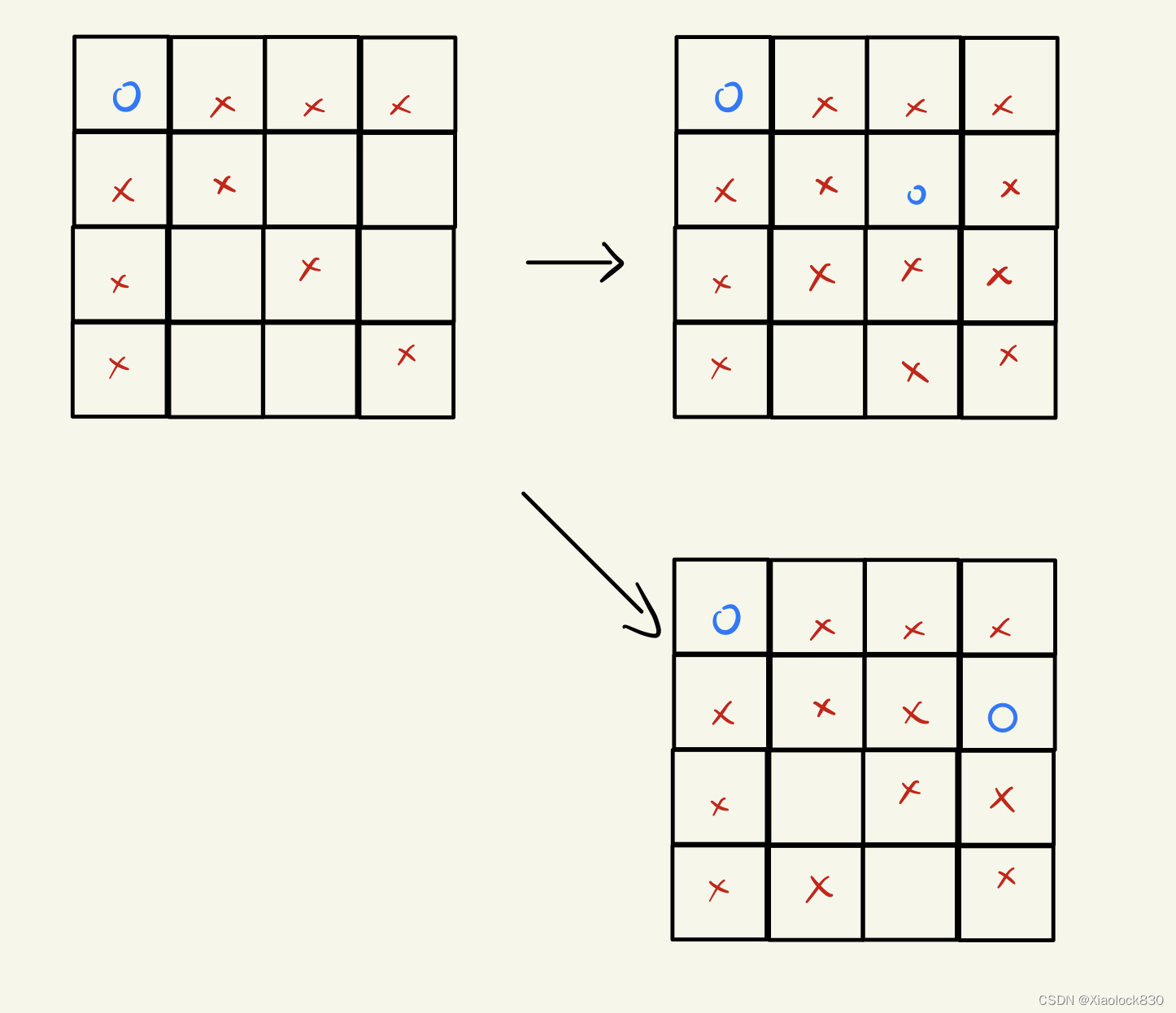
显然这种放法也是只能放三个，那么再次回退到上一个状态，按照顺序将第二个皇后放在第三行第二个（这时和放在第二行第三列是对称的，因此结果一致），显然也只能放四个皇后，状态回溯到上一个状态

再将第二个皇后放在第三行第四列，显然这种情况也是只能最多放三个
在这里插入图片描述
其他两个位置也和上面的位置是对称的，因此将第一个皇后放在第一行第一列的情况是没有结果的，状态回溯到没有放皇后的状态

按照顺序，我们将第一个皇后放在第一行第二位
在这里插入图片描述
再按照顺序将第二个皇后放在第二行第四列

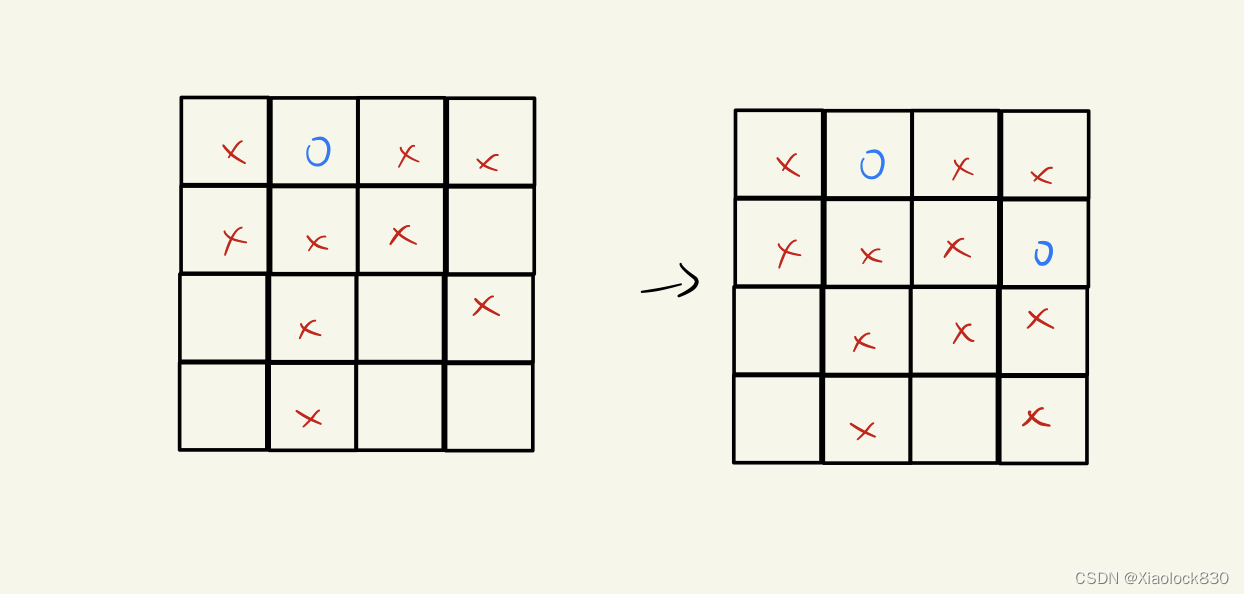
按照顺序将第三个皇后放在第三行第一列上，可以发现这种情况可以放到第四个皇后，状态再次回溯到第一个状态（第一个皇后放在第一行第二列上）

按照顺序，将皇后放在第三行第一列，可以发现最终产生的结果和上一次的结果一样，因此状态再次退回到没有一个皇后的状态

按照顺序，将第一个皇后放在第一行第三列上
在这里插入图片描述
然后按照顺序，将第二个皇后放在第二行第一列上

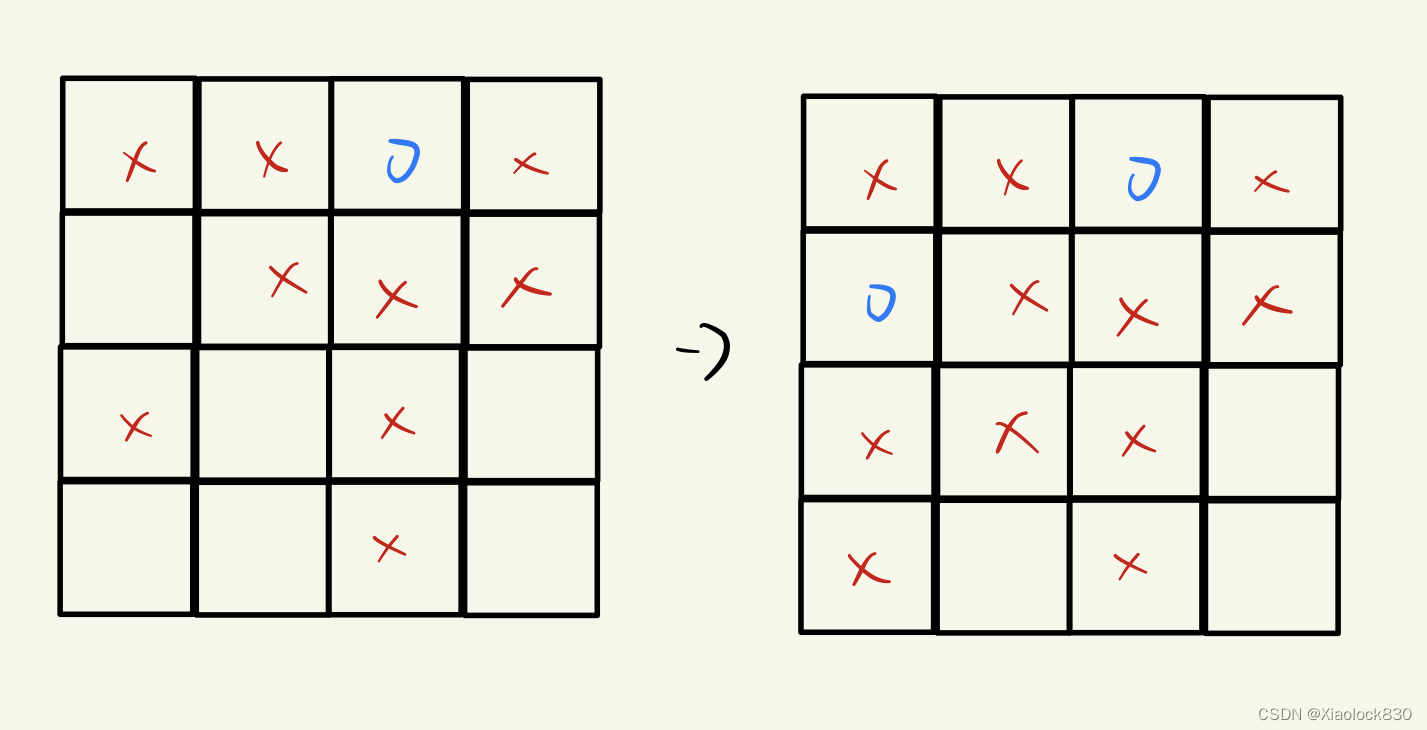
按照顺序，第三个皇后放在第三行第四列上，可以发现最终也可以得到最终的结果

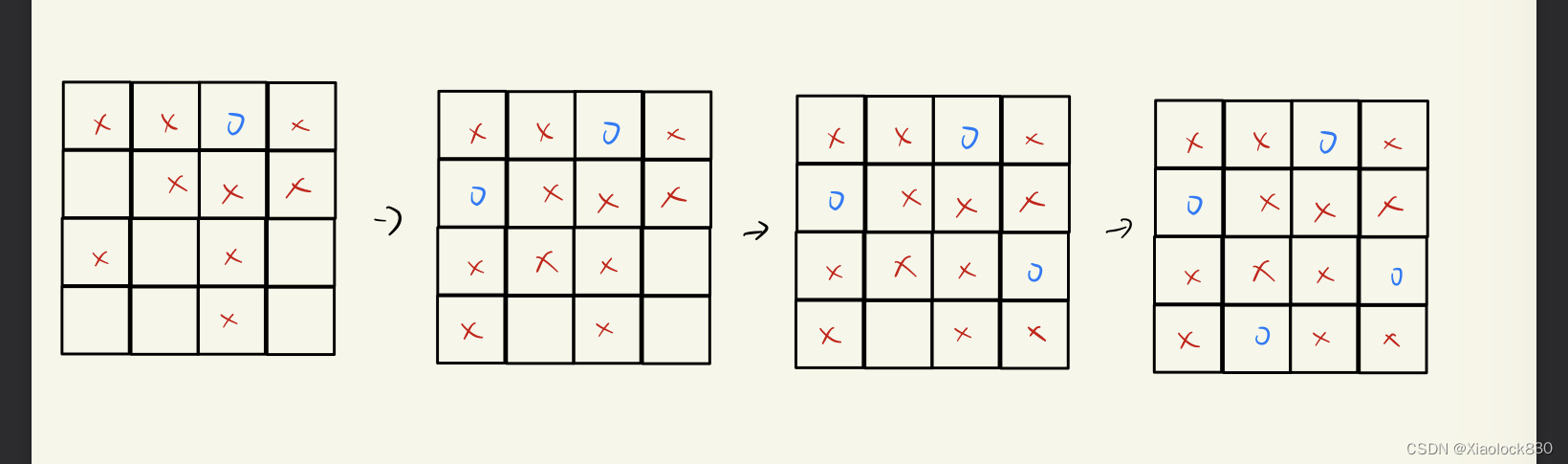
事实上，把第一个皇后放在第一行第三列上和放在第一行第二列上是对称的情况，因此得到的结果也是对称的

而将第一个皇后放在第一行第四列上和放在第一行第一列上是对称的情况，因此也得不到最后的结果

按照上面的思想，可以写出下面的代码

代码

class Solution {
    static class Pair{
        public int x;
        public int y;

        public Pair(int x, int y){
            this.x = x;
            this.y = y;
        }
    }

    static void DFS(List<List<Pair>> result, List<Pair> curRet,
                int curRow, int n){
        //每一行都有元素，当前结果是可行的
        if(curRow == n){
            result.add(new ArrayList<>(curRet));
            return;
        }
        //遍历每一列
        for (int i = 0; i < n; i++) {
            if(isValidPos(curRet, curRow, i)){
                curRet.add(new Pair(curRow, i));
                //处理下一行
                DFS(result, curRet, curRow + 1, n);
                //回溯
                curRet.remove(curRet.size() - 1);
            }
        }
    }

    /**
     * 判断当前位置是否有效
     * @param curRet
     * @param row
     * @param col
     * @return
     */
    private static boolean isValidPos(List<Pair> curRet, int row, int col) {
        //查看每一个已经存储的点与该点是否有冲突
        for (int i = 0; i < curRet.size(); i++) {
            Pair pair = curRet.get(i);
            if(pair.y == col || pair.x + pair.y == row + col ||
                pair.x - pair.y == row - col){
                return false;
            }
        }
        return true;
    }

    private static List<List<String>> transResult(List<List<Pair>> result, int n){
        List<List<String>> finalResult = new ArrayList<>();
        for (int i = 0; i < result.size(); i++) {
            //一种方案
            List<Pair> curRet = result.get(i);
            List<StringBuffer> stringList = new ArrayList<>();

            //先将所有位置都设置为.
            for (int j = 0; j < n; j++) {
                StringBuffer stringBuffer = new StringBuffer();
                for (int k = 0; k < n; k++) {
                    stringBuffer.append(".");
                }
                stringList.add(stringBuffer);
            }

            for (int j = 0; j < curRet.size(); j++) {
                //一种方案中的位置
                Pair pair = curRet.get(j);
                //再将对应位置设置为Q
                stringList.get(pair.x).setCharAt(pair.y, 'Q');
            }

            //重新创建一个ret，存储StringList中StringBuffer.toString后的字符串
            List<String> ret = new ArrayList<>();
            for (int j = 0; j < stringList.size(); j++) {
                ret.add(stringList.get(j).toString());
            }
            finalResult.add(ret);
        }
        return finalResult;
    }

    public static List<List<String>> solveNQueens(int n) {
        List<List<Pair>> result = new ArrayList<>();
        List<Pair> curRet = new ArrayList<>();
        DFS(result, curRet, 0, n);
        return transResult(result, n);
    }
}