第1章 特征工程
1、为什么需要对数值类型的特征做归一化?
(1)消除量纲,将所有特征统一到一个大致相同的区间范围,使不同指标之间具由可比性;
(2)可以加快梯度下降收敛的速度,归一化后让等高线的分布更加均匀,类似于一个圆,减少求解过程中参数寻优的震荡,更加笔直的找到最优解。

常用的归一化方式有两种:
(1)线性函数归一化(min-max scaling):
x
n
o
m
=
X
−
X
m
i
n
X
m
a
x
−
X
m
i
n
x_{nom} = \frac{X-X_{min}}{X_{max}-X_{min}}
xnom=Xmax−XminX−Xmin
将数映射到[0,1]之间,实现对原始数据的等比缩放。但存在量纲,故此方式仅适用于数据不符合正态分布、不涉及距离度量、协方差计算的时候,例如图像处理RGB转化为[0 255]范围。
(2)零均值归一化(z-score normalization):
z
=
x
−
μ
σ
z = \frac{x-\mu}{\sigma}
z=σx−μ
其中
μ
\mu
μ为均值,
σ
\sigma
σ为方差,使特征的均值变为0,方差变为1。将有量纲的表达式变为无量纲的表达式,适用于分类、聚类算法中,需要使用距离来度量相似性或PCA进行降维的时候。
注:决策树模型不适合归一化,它使用的信息增益比跟特征是否归一化无关。
2、怎样处理类别型特征?
类别特征是只能在有限选项内取值的特征,通常以字符串形式输入。故除决策树外,其余模型使用前需要将其转化为数值型特征才能处理。
(1)序号编码(Ordinal Encoding)
使用具有大小关系的数值ID,来处理类别间具有大小关系的数据。例如,低、中、高,会用1、2、3表示。
(2)独热编码(One-hot Encoding)
使用稀疏向量,来处理类别间不具有大小关系的特征。例如,红、黄、蓝用(1,0,0)、(0,1,0)、(0,0,1)。
注意:(1)使用稀疏向量来节省空间(2)配合特征选择来降低维度
(3)二进制编码(Binary Encoding)
是对One-hot的改进,先用序号编码给每个类别赋予一个类别ID,然后将类别ID对应的二进制编码作为结果。
实际上:利用二进制对ID进行哈希映射,最终得到0/1特征向量,且维数少于独热编码,节省空间。
3、什么是组合特征?如何处理高维组合特征?
为提高复杂关系拟合能力,将一阶离散特征两两组合,构成高阶组合特征。
对于高维组合特征可能会面临学习参数规模过大问题,一种处理方式是将组合前的各个特征用更小的低维特征向量来表示,然后用这个低维向量组合特征。(类似于矩阵分解)
4、怎样有效地找到组合特征?
基于决策树的特征组合寻找。
其决策树可采用梯度提升决策树,思想是每次都在之前构建的决策树的残差上构建下一棵决策树。
5、有哪些文本表示模型?它们各有什么优缺点?
6、在图像分类任务中,训练数据不足会带来什么问题?如何缓解数据量不足带来的问题?
数据量不足可能会产生过拟合现象,模型在测试集上的泛化效果不强。
处理方式:
(1)基于模型的方法,采用降低过拟合风险的措施,例如简化模型、正则化等。
(2)基于数据的方法,进行数据扩充(Data Augmentaton),即根据一些先验知识,在保持特定信息的前提下,对原始数据进行适当变换以达到扩充数据集的效果。例如,对图像空间进行变化。对图像进行特征提取后再其特征空间内进行变化,利用通用的数据扩充或上采样技术。借助已有的其他模型或数据进行迁移学习。
7、Word2Vec是如何工作的?它和隐狄利克雷模型有什么区别与联系?
* 补充
8、
第2章 模型评估
1、准确率的局限
2、精确率与召回率的权衡
3、平方根误差的“意外”?
4、什么是ROC曲线?
5、如何绘制ROC曲线?
6、如何计算AUC?
7、ROC曲线相比P-R曲线有什么特点?
8、为什么在一些场景中要使用余弦相似度而不是欧氏距离?
(1)欧氏距离体现数值上的绝对差异,而余弦相似度体现方向上的相对差异。
(2)欧式距离的数值受维度的影响,范围不固定。余弦相似度更关注相对差异,即向量之间的角度关系。不论是在高维还是低维空间,依然保持“相同时为1,正交时为0,相反时为-1”的性质。
(3)例如,用户A(1,0)和用户B(0,1),采用欧氏距离会很小,采用余弦相似度会很大。如果想要表示用户之间的相对差异时,余弦相似度会更好。
再比如,用户A(1,10)和用户(1,100),采用欧氏距离会很大,采用余弦距离会很近。如果更关注数值绝对差异,使用欧氏距离会更好。
9、余弦距离是否是一个严格定的的距离?
10、为什么要进行在线A/B测试?
11、如何进行线上A/B测试?
12、如何划分实验组和对照组?
13、模型评估过程中的验证方法及其优缺点?
14、自助法采样在极限情况下会有多少数据从未被选择过?
15、超参数有哪些调优方法?
16、过拟合和欠拟合具体是指什么现象?
17、能否说出几种降低过拟合和欠拟合风险的方法?
* 补充
18、
第3章 经典算法
1、线性回归
(1)机器学习中有显示解的模型是哪个?
线性回归
2、逻辑回归
3、决策树
决策树是一种自上而下,对样本数据进行树形分类的过程,由结点和有向边组成。结点分为内部结点和叶节点,其中每个内部结点表示一个特征或属性,叶结点表示类别。常被用于分类问题和回归问题。
(1)决策树有哪些启发函数?
从若干不同的决策树中选取最优的决策树是一个NP完全问题,因此长采用启发式学习的方法去构建一颗满足启发式条件的决策树。
常用的决策树算法有ID3(最大信息增益)、C4.5(最大信息增益比)、CART(最大基尼指数)。
ID3:
(1)采用信息增益作为评价指标,会倾向于取值较多的特征。信息增益反映的是给定条件以后不确定性减少的程度,特征取值越多就意味着确定性越高,条件熵越小,信息增益越大。但容易产生过拟合现象,导致泛化能力弱。
(2)ID3只能处理离散型变量。可以再每个节点上产生出多叉分支,且每个特征在层级之间不会复用。
(3)ID3对样本特征缺失值比较敏感。
(4)ID3通过剪枝来权衡树的准确性与泛化能力。
C4.5:
(1)是对ID3进行的优化,引入信息增益比,一定程度上对取值比较多的特征进行惩罚,避免ID3出现过拟合的特性,提升决策树的泛化能力。
(2)C4.5可以处理连续型变量。通过对数据排序之后找到类别不同的分割线作为切分点,根据切分点把连续属性转换为布尔型,从而将连续型变量转换为多个取值区间的离散型变量。可以再每个节点上产生出多叉分支,且每个特征在层级之间不会复用。
(3)C4.5对样本特征缺失值可以处理。
(4)C4.5通过剪枝来权衡树的泛化能力。
CART:
(1)分类回归树(Classification and Regression Tree),不仅可以用于分类,也可以用于回归任务。
(2)CART在构建时每次都会对特征进行二值划分,因此可以很好地适用于连续型变量。CART每个结点只会产生出两个分支,因此最后会形成一颗二叉树,且每个特征可以重复使用。
(3)CART对样本特征缺失值可以处理。
(4)CART直接利用全部数据发现所有可能的树结构进行对比。
(2)如何对决策树进行剪枝?
4、SVM
(1)在空间上线性可分的两类点,分别向SVM分类的超平面上做投影,这些点在超平面上的投影任然线性可分吗?
对于任意线性可分的两组点,它们在SVM分类的超平面上的投影 都是线性不可分的。
方法一: 反证法
使用反证法来证明,若有两组线性可分的点,在超平面上投影和仍然线性可分。那么,可以找到一个更优的超平面将原来的两组点分割开来,但当投影到该超平面时,可以发现投影上的点不能线性分离。(前提SVM仅依赖于支持向量)
方法二: 超平面分离定理(Separating Hyperplane Theorem, SHT)
对于不想交的两个凸集,存在一个超平面,将两个凸集分离。对于二维的情况,两个凸集间距离最短两点连线的中垂线就是一个将它们分离的超平面。
(2)是否存在一组参数使SVM训练误差为0?
(3)训练误差为0的SVM分类器一定存在吗?
(4)加入松弛变量的SVM的训练误差可以为0吗?
(5)线性回归和逻辑回归的区别是什么?
区别:
(1)线性回归处理回归问题,逻辑回归处理分类问题。
(2)逻辑回归的因变量取值是一个二元分布,给定自变量和超参数后,模型学习得到的是因变量的期望,基于此期望来处理预测分类问题。线性回归中求解的是多项式,假设预测模型可以用来近似真实模型,目标便是让预测模型与真实模型之间的误差最小,使用此方式来处理回归问题。
(3)逻辑回归中的因变量是离散的,线性回归中的因变量是连续的。
相同:
(1)二者都使用了极大似然估计来对训练样本建模。线性回归使用最小二乘法,实际上就是在自变量与超参数确定,因变量y服从正态分布的假设下,使用极大似然估计的一种简化。而逻辑回归中通过似然函数的学习来得到最佳的参数。
(2)在求超参数的过程中,都是用梯度下降法。
(6)当使用逻辑回归处理多标签的分类问题时,有哪些常见做法,分别应用于哪些场景,它们之间又有怎样的关系?
第4章 降维
第5章 非监督学习
1、K-means聚类
聚类是在事先并不知道任何样本类别标签的情况 下,通过数据之间的内在关系把样本划分为若干类别,使得同类别样本之间的相 似度高,不同类别之间的样本相似度低。
基本思想:通过迭代方式寻找K个簇(Cluster)的一种划分方案,使得聚类结果对应的代价函数最小。(代价函数通常为欧氏距离)
(1)简述K-means算法的具体步骤
(1)数据预处理,进行归一化(0-1均值、线性均值)、离群点处理(基于统计)
(2)随机选取K个簇中心
(3)定义代价函数(一般为欧氏距离)
(4)进行迭代重复选取每个样本分配到距离最近的簇,然后重新计算簇中心。直至簇中心不再变化或者达到规定的迭代次数。
(2)K-means算法的优缺点是什么?如何对其进行优化
缺点:
(1)受初值和离群点的影响每次的结果不稳定。
(2)结果通常不是全局最优而是局部最优解,效果受初始值的影响大。
(3)无法很好地解决数据簇分布差别比较大的情况
(4)不太适用于离散分类等
优点:
(1)对大数据集,K-means算法相对是可伸缩和高效的,它的计算复杂度是O(NKt)接近于线性,其中N是数据对象的数量,K是聚类的簇数,t是迭代的轮数。
(2)尽管最终得到的是局部最优解,但一般情况下此解已可满足聚类的需求。
调优:
(1)数据归一化和离群点处理
(2)合理选择K值
根据经验或多次试验选取。
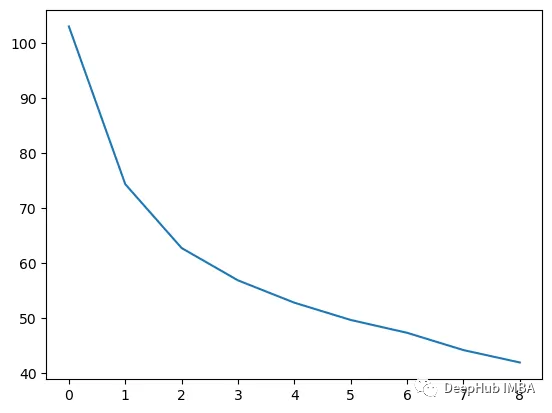
手肘法是一个经验方法,选择拐点处的K值,缺点就是不够自动化。Gap Statistic方法是比先进的方法,可以不需要用肉眼进行判断,而只需要找到最大的Gap Statistic所对应的K值即可,因此该方法也适用于批量化作业。Gap Statistic定义为
G
a
p
(
K
)
=
E
(
l
o
g
D
k
)
−
l
o
g
D
k
Gap(K)=E(logD_k)-logD_k
Gap(K)=E(logDk)−logDk
其中,
D
k
D_k
Dk为分为之前分为K簇时对应的损失函数。
该方法一般通过蒙特卡洛模拟产生,我们在样本所在的区域内按照均匀分布随机地产生和原始样本树一样多的随机样本,并对这个随机样本做K均值,得到一个
D
k
D_k
Dk;重复多次就可以得出
E
(
l
o
g
D
k
)
E(logD_k)
E(logDk)的近似值。
G
a
p
(
K
)
Gap(K)
Gap(K)的物理含义可视为随机样本的损失与实际样本的损失之差。
(3)采用核函数
传统的欧氏距离度量方式,使得K-means算法本质上假设了各个数据簇的数据具有一样的先验概率,并呈现球形或者高维球形分布,但这种分布在实际生活中并不常见。对于非凸的数据分布形状时,可能需要引入核函数来优化,这时的算法称为核K-means算法。
主要思想是通过一个非线性映射,将输入空间中的数据点映射到高维的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
(3)针对K-means算法的缺点,有哪些改进的模型?
K-means++算法
ISODATA算法
(4)证明K-means算法的收敛性
高斯混合模型
第6章 概率图模型
第7章 优化算法
机器学习算法 = 模型表征 + 模型评估 + 优化算法
1、有监督学习涉及的损失函数有哪些?请列举并简述它们的特点。
- 0-1损失函数
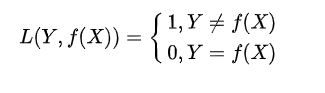
L 0 − 1 ( f , y ) = 1 f y ≤ 0 L_{0-1}(f,y)=1_{fy≤0} L0−1(f,y)=1fy≤0
其中 1 p 1_p 1p 是指示函数,当 p p p 为真时取1, p p p 为假时取0。可以很直观地反映分类的错误率,但由于是非凸、非光滑的特点,使得该算法很难直接对该函数进行优化。
-
Hinge Loss 铰链损失函数(0-1损失函数的代理损失函数)
L h i n g e ( f , y ) = m a x { 0 , 1 − f y } L_{hinge}(f, y) = max\{0, 1 - fy\} Lhinge(f,y)=max{0,1−fy}
其中 f y ≥ 1 fy≥1 fy≥1 时,不对其做任何惩罚输出为0; f y < 1 fy<1 fy<1 时,输出 1 − f y 1-fy 1−fy。通常被用于最大间隔算法(maximum-margin),而最大间隔算法又是SVM(支持向量机support vector machines)用到的重要算法(注意:SVM的学习算法有两种解释:1. 间隔最大化与拉格朗日对偶;2. Hinge Loss)。它是0-1损失函数相对紧的凸上界,但在 f y = 1 fy=1 fy=1 处不可导,因此不能用梯度下降法进行优化,而是用次梯度下降法。

-
Logistic损失函数(0-1损失函数的代理损失函数)
L l o g i s t i c ( f , y ) = l o g 2 ( 1 + e − f y ) L_{logistic}(f, y) = log_2(1 + e^{-fy}) Llogistic(f,y)=log2(1+e−fy)
它是0-1损失函数的凸上界,且该函数出处光滑,可以使用梯度下降法进行优化。但该损失函数对所有的样本点都有所惩罚,因此对异常值相对更敏感一些。
- Cross Entropy交叉熵损失函数( f ∈ [ − 1 , 1 ] f \in [-1,1] f∈[−1,1] 时,0-1损失函数代理函数)
 L
c
r
o
s
s
e
n
t
r
o
p
y
(
f
,
y
)
=
−
l
o
g
2
(
1
+
f
y
2
)
L_{cross \ entropy}(f, y) = - log_2(\frac{1 + fy}{2})
Lcross entropy(f,y)=−log2(21+fy)交叉熵损失函数也是0-1损失函数的光滑凸上界。
L
c
r
o
s
s
e
n
t
r
o
p
y
(
f
,
y
)
=
−
l
o
g
2
(
1
+
f
y
2
)
L_{cross \ entropy}(f, y) = - log_2(\frac{1 + fy}{2})
Lcross entropy(f,y)=−log2(21+fy)交叉熵损失函数也是0-1损失函数的光滑凸上界。

2、凸优化基本概念
(1)机器学习中的优化问题,哪些是凸优化问题,哪些是非凸优化问题?请举例。

凸优化例子:线性回归、Logistic 回归、SVM
非凸优化例子:PCA、深度神经网络模型
、L1正则化与稀疏性
稀疏性说白了就是模型的很多参数为0。相当于是对模型进行依次特征选择后,只留下一些比较重要的特征,提高模型的泛化能力,降低过拟合的可能。
在实际应用中,机器学习模型的输入动辄几百上千万维,稀疏性就显得更加重要,谁也不希望把这上千万维的特征全部搬到先上去,因为在线上可能需要毫秒级的响应时间下完成千万维特征的特区以及模型的预测。
(1)L1正则化使得模型参数具有稀疏性的原理是什么?
L2的正则项约束后的解空间是圆形的,L1的正则项约束的解空间是多边形的。而多边形的解空间更容易在尖角处与等高线碰撞出系数解。
第8章 采样
第9章 前向神经网络
、深度神经中的激活函数
对于线性不可分问题,需要使用非线性变换对数据的分布进行重新映射。对于深度神经网络,我们在每一层线性变换后叠加一个非线性激活函数,以避免多层网络等效于单层线性函数,从而获得更强大的学习与拟合能力。
(1)常用激活函数及其导数
1. Sigmoid
f
(
x
)
=
1
1
+
e
−
x
f(x)=\frac{1}{1+e^{-x}}
f(x)=1+e−x1
对应的导数为
f
′
(
x
)
=
f
(
x
)
(
1
−
f
(
x
)
)
f'(x)=f(x)(1-f(x))
f′(x)=f(x)(1−f(x))
2. Tanh
f
(
x
)
=
t
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}
f(x)=tanh(x)=ex+e−xex−e−x
对应的导数为
f
′
(
x
)
=
1
−
(
f
(
x
)
)
2
f'(x)=1-(f(x))^2
f′(x)=1−(f(x))2
注:Tanh相当于Sigmoid的平移:
t
a
n
h
(
x
)
=
2
s
i
g
m
o
i
d
(
2
x
)
−
1
tanh(x)=2sigmoid(2x)-1
tanh(x)=2sigmoid(2x)−1
3. ReLU
f
(
x
)
=
m
a
x
(
0
,
x
)
f(x)=max(0,x)
f(x)=max(0,x)
对应的导数为
f
′
(
x
)
=
{
1
,
x
>
0
0
,
x
≤
0
f'(x)= \left \{\begin{array}{cc} 1, &x > 0 \\ 0, &x≤0 \end{array}\right.
f′(x)={1,0,x>0x≤0
(2)为什么Sigmoid和Tanh激活函数会导致梯度消失的现象?
Sigmoid和Tanh激活函数的倒数在x趋近于很大或很小时都会趋近于0,从而出现“梯度消失”。

(3)ReLU系列的激活函数相对于Sigmoid和Tanh激活函数有什么优点?它们有什么局限性以及如何改进?
优点
(1)从计算角度来说,Sigmoid和Tanh激活函数需要计算指数,复杂度高,ReLU只需要一个阈值即可得到激活值。
(2)ReLU的非饱和性可以有效地解决梯度消失问题,提供相对宽的激活边界。
(3)ReLU的单侧抑制提供了网络的系数表达能力。
局限性
会导致神经元容易死亡的问题,当负梯度经过ReLU时会被置为0,且在之后不回被任何数据激活。在训练中,如果学习率设置较大,会导致超过一定比例的神经元不可逆转的死亡,进而参数梯度无法更新,整个训练过程失败。
改进
未解决上述问题,设计了LReLU(Leaky ReLU)
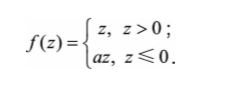
LReLU相对于ReLU来说,在z<0时其值不为0,而是一个斜率为a的线性函数,这个a是一个很小的正常数,这样子既实现了单侧抑制,又保留了部分负梯度信息以至于不会完全丢失。但另一方面,就在于如何确定合适的a值。一般来说会通过多次重复训练来找到合适的值。

进一步改进
PReLU(Paramtetric ReLU):将斜率a作为网络中可学习的参数,进行反向传播训练,与其他含参数网络层联合优化。
RReLU(Random ReLU):增加了“随机化”机制,斜率a作为一个满足某种分布的随机采样,测试时再固定下来。在一定程度上能起到正则化的作用。
、多层感知机的反向传播算法
()平方损失函数和交叉熵损失函数分别适合什么场景?
平方损失函数适合输出为连续型数值,并且最后一层不含Sigmoid或Softmanx激活函数的神经网络.
- 原因:

交叉熵损失适合二分类或多分类的场景。