一、前言

本文主要讲了最短路问题，以及解决最短路问题的Floyd算法概念与两道简单的相关例题。

二、FLoyd算法

1、最短路问题

最广为人知的图论问题。
简单图的最短路径

① 树上的路径：任意2点之间只有一条路径

② 所有边长都为 1 的图：用 BFS 搜最短路径，复杂度O(n+m)

普通图的最短路径

① 边长：不一定等于 1，而且可能为负数

② 算法：Floyd、Dijkstra、SPFA 等，各有应用场景，不可互相替代

【最短路算法比较】

2、Floyd算法

最简单的最短路径算法，代码仅有5行
存图：最简单的矩阵存图
易懂，比暴力的搜索更简单易懂
效率不高，不能用于大图
在某些场景下有自己的优势，难以替代。

def Floyd():
    for k in range(1,n+1):
        for i in range(1,n+1):
            for j in range(1,n+1):
                if dp[i][k]+dp[k][j]<dp[i][j]:
                    dp[i][j]=dp[i][k]+dp[k][j]

3、Floyd的特点

Floyd算法：“多源” 最短路算法，一次计算能得到图中每一对结点之间 (多对多) 的最短路径。
Dijkstra、 Bellman-Ford、 SPFA算法："单源” 最短路径算法 (Single sourceshortest path algorithm)，一次计算能得到一个起点到其他所有点 (一对多) 的最短路径。
在截止目前的蓝桥杯大赛中，Floyd算法是最常见的最短路径算法。

4、Floyd算法思想：动态规划

动态规划：求图上两点 i、j 之间的最短距离，按 “从小图到全图” 的步骤，在逐步扩大图的过程中计算和更新最短路。

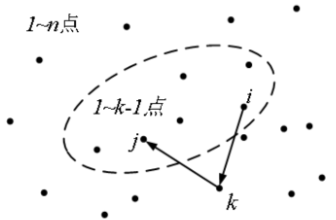
定义状态：dp[k][i][j]，i、j、k 是点的编号，范围 1~n。状态 dp[k][i][j] 表示在包含 1~k 点的子图上，点对 i、j 之间的最短路。

状态转移方程：从子图 1~k-1 扩展到子图 1~k

dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] +dp[k-1][k][j])

虚线圆圈：包含1~k-1点的子图。
dp[k-1][i][j]：虚线子图内的点对 i、j 的最短路；
dp[k-1][i][k]+dp[k-1][k][j]：经过 k 点的新路径的长度，即这条路径从 i 出发，先到 k，再从 k 到终点 j。
比较：不经过 k 的最短路径 dp[k-1][i][j] 和经过 k 的新路径，较小者就是新的 dp[k][i][j]。

k 从 1 逐步扩展到 n：最后得到的 dp[n][i][j] 是点对 i、j 之间的最短路径长度。
初值 dp[0][i][j]：若 i、j 是直连的，就是它们的边长；若不直连，赋值为无穷大。
i、j 是任意点对：计算结束后得到了所有点对之间的最短路。

【方程的简化】（这里留个眼）

dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j])

用滚动数组简化：

dp[i][j]=min(dp[i][j], dp[i][k] + dp[k][j])

【Floyd算法总结】

1）在一次计算后求得所有结点之间的最短距离。
2）代码极其简单，是最简单的最短路算法。
3）效率低下，计算复杂度是 O(n^3)，只能用于 n <300 的小规模的图。
4）存图用邻接矩阵 dp[][] 。因为 Floyd 算法计算的结果是所有点对之间的最短路，本身就需要 n^2 的空间，用矩阵存储最合适。
5）能判断负圈。负圈：若图中有权值为负的边，某个经过这个负边的环路，所有边长相加的总长度也是负数，这就是负圈。在这个负圈上每绕一圈，总长度就更小，从而陷入在负圈上兜圈子的死循环。
Floyd算法很容易判断负圈，只要在算法运行过程出现任意一个 dp[i][j]<0 就说明有负圈。因为 dp[i][j] 是从 i 出发，经过其他中转点绕一圈回到自己的最短路径，如果小于零，就存在负圈。

三、例题

1、蓝桥公园（lanqiaoOJ题号1121）

【题目描述】

小明来到了蓝桥公园。已知公园有 N 个景点，景点和景点之间一共有 M 条道路。小明有 Q 个观景计划，每个计划包含一个起点 st 和一个终点 ed，表示他想从 st 去到 ed。但是小明的体力有限，对于每个计划他想走最少的路完成，你可以帮帮他吗？

【输入描述】

输入第一行包含三个正整数 N, M, Q。第 2 到 M+1 行每行包含三个正整数 u, v, w，表示 u、v 之间存在一条距离为 w 的路。第 M+2 到 M+Q-1 行每行包含两个正整数 st, ed，其含义如题所述。

1<=N<=400, 1<=M<=N*(N-1)/2, Q<=10^3, 1<=u, v, st, ed<=n, 1<=w<=10^9

【输出描述】

输出共 Q 行，对应输入数据中的查询。若无法从 st 到达 ed 则输出 -1。

def floyd():
    global mp
    global N
    global M
    global Q
    for k in range(1,N+1):
        for i in range(1,N+1):
            for j in range(1,N+1):
                mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j])
        
N,M,Q=map(int,input().split())
mp=[[1100000000]*(M+2) for _ in range(N+2)]
for _ in range(M):
    u,v,w=map(int,input().split())
    w=min(mp[u][v],w)               #考虑重边，选最小权值那条
    mp[u][v]=w
    mp[v][u]=w
floyd()
for _ in range(Q):
    st,ed=map(int,input().split())
    if mp[st][ed]==1100000000:      #st无法到达ed
        print(-1)
    elif st==ed:                    #有可能兜一圈回到起点呢，所以要特判
        print(0)
    else:
        print(mp[st][ed])

2、路径（2021年初赛 lanqiaoOJ题号1460）

填空题

【题目描述】

小蓝的图由 2021 个结点组成，依次编号1至2021。对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为75。

请计算，结点 1 和结点 2021 之间的最短路径长度是多少。

【常规的floyd】：运行时间长达30分钟！

from math import *
def lcm(x,y):
    return x//gcd(x,y)*y    #求最小公倍数
dp=[[int(0x3f3f3f3f3f3f3f3f) for _ in range(2022)] for _ in range(2022)]

def floyd():
    global dp
    for k in range(1,2022):
        for i in range(1,2022):
            for j in range(1,2022):
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])

for i in range(1,2022):
    for j in range(1,2022):
        if abs(i-j)<=21:
            dp[i][j]=lcm(i,j)
floyd()
print(dp[1][2021])

【简化版floyd】

from math import *
def lcm(x,y):
    return x//gcd(x,y)*y    #求最小公倍数
dp=[[int(0x3f3f3f3f3f3f3f3f) for _ in range(2022)] for _ in range(2022)]

def floyd():
    global dp
    for k in range(1,2022):
        #for i in range(1,2022):
        for i in range(1,2):
            for j in range(1,2022):
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])

for i in range(1,2022):
    for j in range(1,2022):
        if abs(i-j)<=21:
            dp[i][j]=lcm(i,j)
floyd()
print(dp[1][2021])

我们只求点 1 到其他点的最短路就行！这实际上这变成了 Bellman-ford 算法。

【Bellman-ford更简洁的写法】

from math import *
def lcm(x,y):
    return x//gcd(x,y)*y    #求最小公倍数
dp=[int(0x3f3f3f3f3f3f3f3f)]*2022   #dp[i]:点i到点1的最短路径
d[1]=0
for i in range(1,2022):     #点i
    for j in range(i+1,i+22):   #和i有边的点j
        if j>2021:
            break
        dp[j]=min(dp[j],dp[i]+lcm(i,j))     #更新最短路
print(dp[2021])

以上，FLoyd算法的入门与应用

祝好

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/387556.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！