❤️作者主页:微凉秋意
✅作者简介:后端领域优质创作者🏆,CSDN内容合伙人🏆,阿里云专家博主🏆
✨精品专栏:C++面向对象
🔥系列专栏:数据结构与课程设计
文章目录
- 🔥前言
- 串的基础知识
- 串的存储结构
- 顺序存储
- 链式存储
- 基本操作的实现
- 求子串
- 字符串比较
- 返回子串位置
- 字符串模式匹配
- 朴素模式匹配算法
- KMP 算法
- 求 next 数组(手算)
- next 数组优化为nextVal
🔥前言
今天补充数据结构专栏的文章,前阵子一直在准备考研,期间也是复习了很长时间的数据结构知识,对于一些结构也有了更深刻和独特的理解。今天就把有关 “串” 的基本操作以及比较热门的
KMP算法做一个系统的总结,后期也会更新树、图以及考研热门算法的文章,建议大家订阅学习。
串的基础知识
先了解有关串的一些知识,方便以后遇到某些术语时能够心领神会。
串的定义:
串,即字符串(String)是由零个或多个字符组成的有限序列,串中的字符个数n称为串的长度。n = 0 时的串称为空串
串的术语:
子串:串中任意个连续的字符组成的子序列。
主串:包含子串的串。
字符在主串中的位置: 字符在串中的序号。
子串在主串中的位置:子串的第一个字符在主串的位置
比如:
S = ‘iPhone 11 Pro Max?’
‘iPhone’ 和 'Pro M' 都是串 S 的子串,S 是子串‘iPhone’ 的主串
'1' 在S 中的位置是8(第一次出现,下标从1开始计算)
字符集编码:每个字符在计算机中对应一个二进制数,比较字符的大小其实就是比较二进制数的大小,这点在后续的字符串比较方法中会有体现。
串的存储结构
顺序存储
采用静态数组实现(定长顺序存储):
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN]; // 每个分量存储一个字符
int length; // 串的实际长度
}SString;
采用动态数组实现(堆分配存储):
typedef struct {
char* ch;
int length;
}HString;
// 初始化操作
HString S;
S.ch = (char*)malloc(MAXLEN * sizeof(char)); // 使用堆分配,使用过后需要手动 free 掉
S.length = 0;
在我们自己定义串的时候可以在
ch[0]的位置存储串的长度,这样可以使字符的位序和数组的下标相同,但是要注意此时的长度取值范围仅在0~255之内,这是char类型能存储的最大长度。
链式存储
链式存储的形式一般都与单链表的存储形式一致,所以牢固掌握单链表很重要,有关文章在此专栏也有提供。
typedef struct StringNode {
char ch; // 每个结点存一个字符
struct StringNode* next;
}StringNode, *String;
如果每个结点只能存储一个字符,这样的数据结构的存储密度就太低了,因为 32 位操作系统下指针的大小为 4 个字节。因此可以适当的提高每个结点的存储容量,如:
typedef struct StringNode {
char ch[8]; // 每个结点存多个字符
struct StringNode* next;
}StringNode, *String;
顺序存储和链式存储的优缺点可以参考链表和顺序表的优缺点,从增删改查的效率上考虑即可。
基本操作的实现
这里采用顺序存储的方式来实现基本操作,即:
#define MAXLEN 255
typedef struct {
char ch[MAXLEN];
int length;
}SString;
另外,舍弃ch[0],从下标 1 开始存储字符。
求子串
对应方法:SubString(&Sub,S,pos,len):用Sub 返回串 S 的第pos 个字符起长度为 len 的子串
具体实现:
bool SubString(SString& Sub, SString S, int pos, int len) {
if (pos + len - 1 > S.length) // 子串越界
return false;
for (int i = pos; i < pos + len; i++) {
Sub.ch[i - pos + 1] = S.ch[i]; // 左边从下标 1 开始赋值
}
Sub.length = len;
return true;
}
字符串比较
对应方法:StrCompare(S,T):若S>T,则返回值>0;若S=T,返回值=0,若小于,则返回值<0
具体实现:
int StrCompare(SString S, SString T) {
for (int i = 1; i <= S.length && i <= T.length; i++) {
if (S.ch[i] != T.ch[i]) // 如果不相等,直接用减法的结果当成比较结果
return S.ch[i] - T.ch[i];
}
return S.length - T.length; // 此时比较字符串长度,用减法结果表示即可
}
返回子串位置
对应方法:Index(S,T):若主串S中存在与串T值相同的子串则返回他在主串中第一次出现的位置,否则返回0。
具体实现:
int Index(SString S, SString T) {
SString P;
for (int i = 1; i <= S.length - T.length + 1; i++) {
SubString(P, S, i, T.length);
if (StrCompare(P, T) == 0) {
return i;
}
}
return 0;
}
这里稍微的“偷懒”了一下,但是代码逻辑很清晰:
- P 串是主串 S 中长度为 T串长度的子串,赋值方法当然是通过调用之前写的获取子串方法
- 循环中 i 没必要走到主串的长度,只要 i 加上 T 的子串长度不大于 主串即可
- 调用字符串比较函数,只要P 与 T 相等,返回 i 值就是子串在主串中第一次出现的位置
字符串模式匹配
定义:在主串中找到与模式串相同的子串,并返回其所在位置。
两种算法:朴素模式匹配 与 KMP 算法
朴素模式匹配算法
这种方式可以称之为暴力解法:
- 我们从主串开始遍历,如果位序 1 不匹配,那么从2开始匹配;如果位序1至3都匹配,位序4不匹配,那么主串还是要从位序2继续匹配,而模式串回到位序1
- 因此每次的模式串都要从位序1遍历,而主串的位序会比上一次的位序多1
- 只要处理好主串的位序问题,那么就能暴力解题
具体算法:
int commonCompare(SString &s1, SString &s2) {
int i,j;
for (i = 1, j = 1; i <= s1.length,j <= s2.length;) {
if (s1.ch[i] == s2.ch[j]) {
i++, j++;
}
else {
i = i - j + 2; // 理解此行代码很重要,此写法可以让位序逐渐加 1
j = 1;
}
if (j > s2.length)
return i - s2.length;
}
return 0;
}
KMP 算法
KMP 算法比起朴素匹配算法多了一个重要的 next 数组,而且该数组与主串没有任何关系,我们需要通过模式串来求出 next 数组作为模式串指针指向的重要依据,而且主串的指针不回溯。
图示:

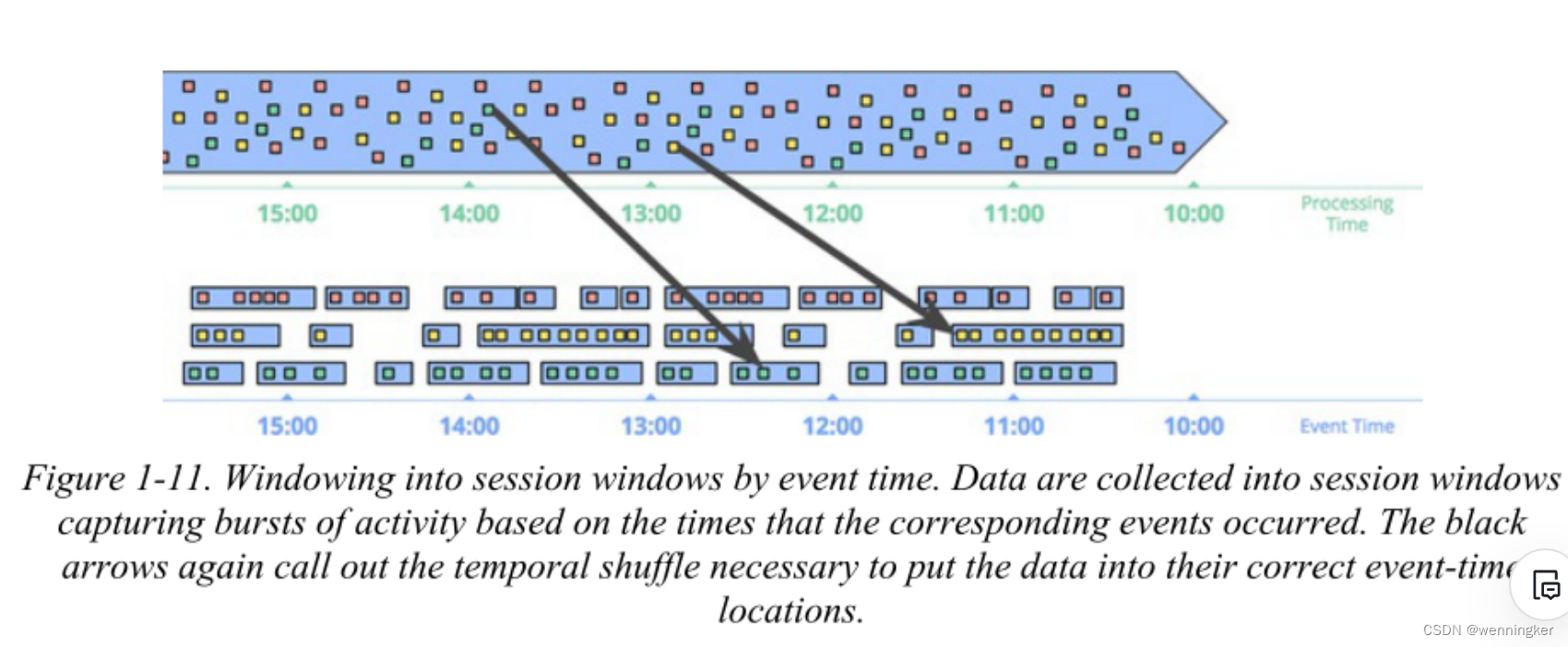
这里我们可以明显看到前四个字符都是匹配的,如果按照朴素模式匹配算法的逻辑,下一次主串指针会指向2,模式串指向1,重复朴素模式匹配操作;但实际上我们是可以知道主串前四个字符与模式串是对应的,因此不必让模式串指向1,而是将模式串向右 “移动”,如果模式串指向3,那说明前两个字符为a、b,这与主串a、a,并不对应,因此可以让模式串指向2,a 与 a 是对应的,那么下一步就是比较 b 与主串的第五个字符,时间效率提高了不少。
具体算法实现:
int Index_kmp(SString& S, SString& T, int next[]) {
int i = 1, j = 1;
while (i <= S.length && j <= T.length) {
if (S.data[i] == T.data[j] || j == 0) {
i++;
j++;
}
else {
j = next[j]; // 模式串的指向改变
}
if (j > T.length) {
return i - T.length;
}
else
return 0;
}
}
求 next 数组(手算)
上面也提到 next 数组是KMP 算法中的核心,因此一定要会手算该数组,其代表的也是当模式串在 j 位置不匹配时,下一步应该指向的位置:j = next[j]。以下图为例:

如果第一个位置就不匹配,那就让 next[j] 的值为0,在写算法时如果 j 为0,那就让主串和模式串的指针都加1 即可;如果第二个位置不匹配,直接让 next[j] 为1,也就是让模式串的第一个和主串的第二个字符比较。以后写 next 数组时,指针1和2的位置分别无脑写0和1。
对于此例也是一样,现在看位序3失配时,next 该为多少:
主串与模式串前两个字符都是 a和b,显然模式串右移一位后a与b并不匹配,因此位序3的next 应为 1。
对于位序4:
前三个字符均为aba,因此模式串移动两位后的 a 可以与主串第三位对应,所以位序4的next应为2。
对于位序5:
右移两位后虽然 a 与 a 对应,但是随后的 b 与 a 不对应,所以其next 还是 2。
对于位序6:
模式串的 ab 与 主串的 ab 对应,因此其 next 为3。
即 next[7] = { ,0,1,1,2,2,3},next[0]舍弃不用。
next 数组优化为nextVal
KMP 算法的优化实际上也就是对next 数组的优化,优化思路如下:

比如第三个位序不匹配时,我们除了知道两者的前两个字符为 ab 外,其次可以知道主串的第三字符一定不是 a,那么模式串的第一个字符 a 就没必要再去和主串的第三个字符比较了,直接让 next 的值为0,下一步主串和模式串的指针都加1。
其余位序也是以同样的思维得到,我算出的数组为:
nextVal[7] = { ,0,1,0,2,1,3}
给出对应的转换函数:
// 优化 next 为 nextVal
void optimize_next(int next[],int nextVal[],SString &T) {
nextVal[1] = 0; // 无脑写0
for (int j = 2; j <= T.length; j++) {
// 字符相等,nextVal 的值应为前面字符对应的nextVal
if (T.ch[j] == T.ch[next[j]]) {
nextVal[j] = nextVal[next[j]];
}
else {
// 字符不等,无法优化,继承next数组的数据即可
nextVal[j] = next[j];
}
}
}
那么到此 串 的知识、基本操作的实现、朴素匹配和KMP算法以及优化就总结完毕了,重点是掌握KMP算法中的手算 next 数组,大家可以自己找主串和模式串进行练习,彻底掌握 KMP 算法。