机器学习管道中的数据定价

Data Pricing in Machine Learning

作者：Pipelines Zicun Cong · Xuan Luo · Pei Jian · Feida Zhu · Yong Zhang

Abstract

机器学习具有破坏性。同时，机器学习只能通过多方协作，在多个步骤中取得成功，就像生态系统中的管道一样，例如为可能的机器学习应用程序收集数据，多方协作培训模型，以及向最终用户提供机器学习服务。数据至关重要，并且渗透到整个机器学习管道中。由于机器学习管道涉及多方，并且为了取得成功，必须形成一个建设性和动态的生态系统，市场和数据定价是连接和促进这些多方的基础。在本文中，我们调查了机器学习管道中数据定价的原则和最新研究进展。我们首先简要回顾一下数据市场和定价需求。然后，我们将重点放在机器学习管道中的三个重要步骤中进行定价。为了了解训练数据收集步骤中的定价，我们回顾了原始数据集和数据标签的定价。我们还在机器学习模型的协作训练步骤中调查了定价，并在机器学习部署步骤中概述了最终用户的机器学习模型定价。我们还讨论了一系列可能的未来方向。

关键字 数据资产 · 数据定价 · 数据产品 · 机器学习 · AI

1.Intro

  构建机器学习市场需要多方合作。

  数据对于机器学习至关重要，机器学习模型尤其是深度模型，依赖于大量的数据进行训练测试。机器学习后续的部署、更新、维护也需要数据的参与。

  获取数据对于机器学习而言远非易事。对于构建机器学习模型的一方而言，有如下挑战：（1）开发训练数据集：收集数据、创建适当标签，确保数据质量的成本都比较高。（2）没有必需的训练数据集：这往往意味着要探索所需数据的外部来源，获取外部数据。（3）向他方提供机器学习服务：需要交换数据。

  由于数据和模型在机器学习管道中是必不可少的，数据和模型交换是多方之间最基本的交互，数据和模型市场成为机器学习管道和生态系统的自然选择，定价成为机器学习管道的核心机制。

  数据产品指的是从数据集派生出来的产品和信息服务。数据商品化促使数据所有者共享他们的数据集用以换取报酬，帮助买方获取高质量，大体量的数据产品。

  Agarwal等人[1]总结了五个属性，使数据成为一种独特的资产。（1）可以以零边际成本复制数据。（2）数据的价值本质上是组合的。（3）数据的价值在不同买家之间差异很大。（4）数据的有用性在于从中得出有价值的信息，这很难先验。由于这些特性，实物商品的定价模型不能直接应用或直接扩展到数据产品，因此需要开发新的原理、理论和方法。

  本文重点关注机器学习模型的管道构建里的三个关于数据和模型供应任务的步骤。分别是：数据收集（定价原始数据集和定价数据标签）、机器学习模型训练（关于提供的数据的贡献定价）、模型部署（定价机器学习模型）

具体如下：

1. 定价原始数据集。构建机器学习模型的第一步是收集训练数据，商品化数据可以很好地用于交易从而获取训练数据集。定价原始数据集的挑战在于：如何设置反映数据集有用性的价格。此外定价模型还可以依据不同的目标（收入最大化、无套利、真实性）进行优化，不过这也是个挑战。

2. 定价数据标签。现在常用众包来实现标签获取，不过这面临一个关键挑战：如何顾及标签的准确性并补偿相应的众包参与人员。这项任务常出现在监督学习中。

3. 协调机器学习中的收入分配。协作进行机器学习很热门，这就会出现多个数据的所有者将数据聚合起来进行模型训练，并共享销售这些模型的收入，但数据集的贡献程度会有差异，因此需要公平的奖励数据所有者的贡献

4. 定价机器学习模型。顾客可以直接购买训练好的机器学习模型。但模型可能会有版本的差异，这也会涉及到价格的差异。

  上述四个任务都是将数据产品的价格与其关联的事务联系起来给客户。但是，由于这些任务有不同的应用场景和定价目标，因此它们是通过正交技术来解决的。

  前两个任务中的现有模型旨在为具有绝对效用函数的训练数据集定价，即数据产品的效用仅取决于产品的属性。重要区别是关于效用函数。由于缺乏基本事实验证，数据标签的效用（例如准确性）很难计算。
第三个任务通过数据集对机器学习模型的边际贡献来评估数据集的效用。因此一个数据集的效用害取决于用于共同构建模型的其他数据集的效用。
最后一个任务的现有方法也采用绝对效用函数。但机器学习模型和数据集具有不同属性，因此开发了新的定价模型。

  当机器学习模型和数据集以端到端的方式定价时，这四个任务是相连的。

2.数据市场与定价

2.1.数据市场

  数据市场是一个允许人们购买出售数据的一个平台。例如，Dawex，Snowflake data marketplace，BDEX，Muschalle 等等。

  数据市场的七类参与者：分析师、应用程序供应商、数据处理算法开发人员、数据提供商、顾问、许可和认证实体以及数据市场所有者。

  数据市场的概念架构：

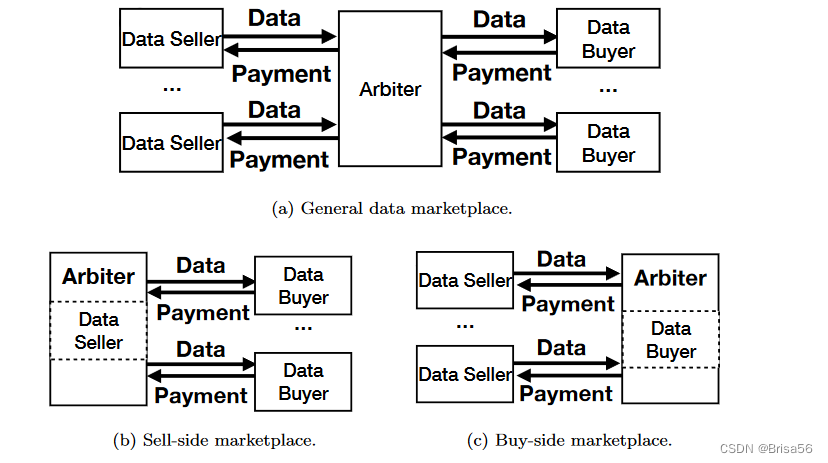
  图a，一般数据市场。数据市场主要由三个实体组成，数据卖方，仲裁者（也称作数据供应商和数据经纪人），数据买方。仲裁器从数据卖家收集数据产品并将其销售给数据买家，买家付款后仲裁者将钱款分发给数据卖方。一般而言，仲裁者被构建为数据市场中的非盈利参与者。

  图b，卖方数据市场。卖方数据市场为一个数据卖方和多个数据买方。卖方市场中，仲裁器由垄断的数据卖方操作，以销售单个卖方的数据产品。在查阅到的文献中，卖方市场由一般数据集和特定类型的数据产品（如XML文档和关系数据库上的数据查询）的定价模型来考虑。

  图c，买方数据市场。买方数据市场有多个数据提供者和一个数据买家。仲裁器由单个数据买方操作，用以从数据供应商处购买数据产品。许多现有研究都考虑了买方市场。例如，deAlfaro等人研究了一个买方市场，其中单个消费者向众包工人支付标签，以标记单个买方的数据集。

2.2.定价策略

  3个重要类别：基于成本的定价，基于客户价值的定价，基于竞争的定价。

• 基于成本的定价

  • 产品的价格是通过在成本中添加特定数量的加价来确定。
  • 常在个人数据定价中采用，其中成本是对数据所有者的总隐私补偿。
  • 缺点：只考虑内部因素，没有考虑外部因素（竞争，需求等）

• 基于客户价值的定价

  • 主要根据目标客户认为的产品价值来确定产品价格
  • 卖方需要通过客户的意愿和支付能力来估计客户对产品的需求
  • 最常用的数据定价策略

• 基于竞争的定价

  • 根据竞争对手的价格水平和行为预期战略性的确定产品价格
  • 博弈论提供了强有力的工具来实现这种策略，比如非合作博弈：每个卖家都是自私的，并独自设立使卖家利润最大化的价格，竞争的结果要是每个卖家的要价达到纳什均衡。

  还有一些其他定价策略，如以运营为导向的定价，以收入为导向的定价，以关系为导向的定价等等。

2.3.四类数据市场

  Fricker和Maksimov提出了四类数据市场：垄断市场、寡头垄断市场、竞争激烈的市场，买主垄断市场。

• 首先，在垄断中，供应商拥有足够的市场力量来设定价格以最大化利润。
• 其次，在寡头垄断中，少数供应商主导着市场。
• 第三，在竞争激烈的市场中，个别供应商没有足够的市场力量来设定利润最大化的价格，价格往往与边际成本保持一致。
• 最后，在买方垄断中，单个买方作为卖方提供的产品的唯一消费者控制市场。

  大多数研究都假设存在显性或隐性的垄断(买方垄断)市场结构中的数据卖家(数据买家)不关心与他人竞争。Balasubramanian等人考虑了寡头市场中的数据定价。Jiang等人研究了一个完全竞争市场，参与者之间可以直接进行交易。

2.4.数据定价的需求

  来回顾Pei等人提出的六个数据定价的需求。

• 真实性

  • 在真实市场中，所有参与者都是自私的，只提供其最大化效用价值的价格。
  • 真实的市场保证，每个参与者都提供其真实的估值才是一个最佳策略。
  • 真实性简化了所有参与者的策略，并确保了市场的基本公平。

• 收入最大化

  • 收入最大化是一种通过较低价格增加客户量的策略。
  • 被新兴市场的卖家广泛采用，用以建立市场份额和声誉。

• 公平性

  • 在某些情况下，卖方需要合作参与交易。如果联盟产生的收入在卖方之间公平分配，那么数据市场对联盟中的参与者是公平的。

  • 假设一组卖家D=[s1,s2,…,sn]合作参与的交易得到了收款v。Sharply举出了公平分配的四条公理:

    • 平衡（有效性）：v需要完全分发给D中的卖家。（计算出各个节点的Shapley值最终的和应该与总体联盟的总利益相等，否则无效）
    • 对称性：相同贡献的卖家应该获得相同的钱。
    • 零元素（冗元性）：如果某一卖方的数据对于联盟获得支付v毫无贡献，则不应受到任何货款。
    • 可加性：如果一组卖家的数据可以用于两个任务t1和t2，分别支付v1和v2，那么解决这两个任务t1 + t2的支付应该是v1 + v2。

  • Shapley值的是一种利益分配的方法，按贡献来评估如何分配利益，贡献越大，收益相对越多。事实证明Shapley值ψ(s)是满足四个公理的唯一分配方法。

  • Shapley值ψ(s)定义为对卖方S⊆D\{si}的所有可能子集si的平均边际贡献
    

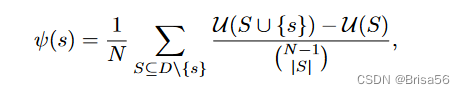
    U(·)是效用函数。上述函数还可以改写为如下形式：
    

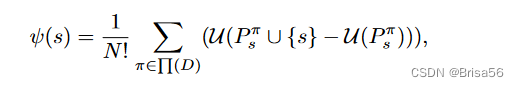
    π ∈ ∏(D)，是一组卖家的排列；
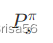
    是π中在卖家s之前的卖家集合。

  • Shapley值具有独特的Shapley公平性，结合其支持不同效用函数的灵活性，使其成为实现公平数据市场的流行工具。

• 无套利定价

  • 套利是利用多个市场之间的价格差异进行的活动。
  • 在数据市场中，数据销售者可能提供多个版本的产品。买家可能会通过购买一些更便宜的产品来规避本身想买的产品的广告价格，这会对卖家产生负面影响。
  • 理想的定价函数应该保证没有套利的可能性。

• 隐私保护

  • 数据市场中，买方、卖方、相关第三方的隐私非常脆弱，可能会以不同的方式披露。
  • 重点关注隐私补偿：出于隐私保护的目的，敏感数据集通常与注入的随机噪声进行交易。具有较少随机噪声的数据集更准确，但可能会泄漏更多隐私，因此应该对数据所有者进行更多补偿。

• 计算效率

  • 有效的计算大量商品和参与者的价格是定价模型的基本要求。
  • 价格应该在关于参与者的数量或数据产品的数量多项式时间内计算。然而，在某些应用场景中，计算具有理想属性的定价函数需要指数级的时间，例如Shapley公平、无套利和收入最大化。
  • koulis等人表明，在关系数据库上计算连接查询的无套利价格通常是NP-hard的。如何有效地确定理想属性的价格是一个技术挑战。

这里提出一个新的机制。

• 贡献激励
  • 众包数据时，一个主要的挑战就是如何确保中报参与者投入精力并提供准确答案。若每个任务只有一个固定价格，那么会有可能参与者值随意提供一个价格，甚至没有解决任务。
  • 一个可取的办法就是众包任务设计适当的奖励，这些任务促使参与者投入努力并提供更高质量的答案。

3.定价原始数据集

针对定价原始数据集，现有的研究考虑四种情形：
  最传统的方法，将数据集作为不可分割的单位，不考虑供应商之间的竞争，数据集的内在属性是决定价格的因素。
  第二种情况，研究如何在竞争市场中对不可分割的数据集进行定价。
  第三种，消费者可以购买整个数据集的一小部分，对消费者而言更灵活了，但会存在套利问题。
  最后一个场景通过隐私补偿对个人数据进行定价

3.1.定价一般数据

机器学习和统计模型容易受到低质量数据的影响。基于质量的数据集定价成了一个自然而然的选择。

  Heckman等人定义了一些列用于衡量数据质量的因素，比如数据的年代、数据准确率、数据量。提出了一个线性模型。将数据集的价格设置为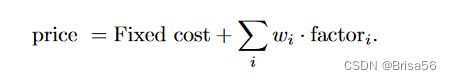
估计模型参数wi是一项艰巨的任务。因为许多数据集没有与之关联的公开价格。

  Yu和Zhang研究了由不同数据质量因素构建的数据集的多版本交易问题。他们假设客户的需求和不同版本的最高可接受价格是公开的。建立了一个双层编程模型来解决这个问题。在第一级，数据卖方确定版本及其价格， 以最大限度地提高总收入。在第二层，一组买家选择数据产品以最大化其效用。求解双层编程模型非常困难。Yu和Zhang[107]提出了一种启发式遗传算法，以数字方式接近它。

3.2.定价众包数据

众包，可以快速低廉的获得机器学习模型的大量训练数据。在众包市场中，任务请求者启动数据收集任务，并根据参与人员报告的成本对其进行补偿。由于工人可能夸大他们的成本，定价模型应该激励工人如实披露他们的成本。

  Yang等人设计了一个用于移动传感数据的反向拍卖机制。这个模型是真实的（如果所有卖家如实报告他们的收集成本）、理性预期的（如果所有卖家都没有负的净利润）、有利的（如果所有买家都没有负的净利润）。
  作者假设一个买方有传感任务集Γ=[T1,T2,…Tn]，每一个任务Ti对与买方他自己有一个价值vi。每一个卖方si选择Γ中的一个任务Γi来完成，对应有一个成本ci。卖方si出价bi卖该数据并提交一个任务投标组（Γi,bi）给买方。在收集完所有投标后，买家选择卖家S的一个子集作为获胜者，并确定支付酬劳pi给每一个胜方si。
  提出的拍卖机制，MSensing，以贪婪的方式选择赢家S。最开始S=∅，它迭代的选择带来了最大非负边际效应的卖家作为胜方。每一个胜方si∈ S都被支付pi。（si的出价bi高于pi将不会赢得拍卖）。具体来说，MSensing在用户S ’ = U \ {si}上运行胜者选择算法。报酬pi是si可以出价的最大价格，这样si就可以在S’中替换一个用户。请注意pi≥bi，这是因为由于成本信息不完整，买方在报价的基础上对卖方提供额外补偿，以激励卖方披露实际成本。MSensing满足了Myerson对真实拍卖机制的描述。

  Jin等人后续工作认为数据购买者对每个传感任务tj都有相应的数据质量要求Qj。作者们提出了一个Vickrey-Clarke-Groves机制，就像真实的反向组合拍卖一样。他们假设每个卖方的数据质量qi是公开的，并且qi对于所有传感任务都是相同的。作者首先考虑了每个卖方仅竞标一组传感任务Γi的情况。拍卖胜方S必须满足每个任务ti的质量要求，也即∑si∈S, 若 tj∈Γi qi ≥ Qj。拍卖的目的是最大限度地提高买卖双方的总效用。作者证明了该设置下的胜者确定是NP-hard，并提出了一种贪婪的胜者选择算法，该算法具有保证与最优总效用的近似比。每位获奖者均由获奖者的关键付款支付。作者在更一般的场景中进一步研究了总效用最大化问题，其中每个卖方都可以竞标多个任务包。他们提出了一种迭代降序算法，可实现接近最优的总效用。但是，拍卖并不真实。

  Koutsopoulos考虑了和Jin等人类似的设置，但是假设一个数据买方只有一个传感任务。作者提出了一个真实的反向拍卖，在保证数据质量要求的同时最大限度降低买方的预期成本。作者假设数据买方事先了解每个卖方的单位参与成本ci的分布。si 的参与单位 xi 是一个正实值，表示从 si 购买了多少数据。给定卖方的出价，数据买方通过求解线性规划模型来确定拍卖获胜者及其参与单位，该模型在数据质量约束下最小化了总预期付款。向选定的获奖者支付关键款项。所有如实竞标的卖家都形成贝叶斯纳什均衡。

3.3.定价数据查询

基于查询的定价模型根据用户的需求量身定制数据购买。客户可以通过数据查询购买数据集中他们感兴趣的部分，并根据他们发出的查询收费。虽然这种市场机制为买方提供了更大的灵活性，但设计不够仔细的定价模式可能会为套利打开漏洞，使买方能够以低于公布价格的成本获得查询结果。

  给定一个数据库 D 和多个查询包 S = { Q1，… … ，Qm } ，如果 Q 的答案只能从 S 中查询包的答案中计算出来，则查询包 Q 由 S 决定。如果广告价格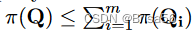
则定价函数是无套利的，也就是说，不能从另一组查询包中更便宜地得到一个查询包 Q 的答案。

  第一个无套利的基于查询的数据定价的正式框架是由 Koutis 等人提出的。其主要思想是，数据卖方首先可以指定一个数据库上的几个视图 V 的价格，然后通过算法来决定一个查询包 Q 的价格。从理论上证明了如果 V 中的视图之间不存在套利情形，则存在唯一的无套利和无折扣的定价函数 π (Q)。具体来说，π (Q)是确定 Q 的 V 的最便宜子集的总价格，这可以通过查询确定性找到。它们还显示了评估价格函数的复杂性。遗憾的是，对于大量的实际查询，定价模型是 NP-hard的。他们为特定类别的连接查询、链式查询和循环查询开发了多项式时间算法。

  随后，Koutis 等基于上述想法开发了一个原型定价系统，QueryMarket。他们将定价模型表示为一个整数线性规划(ILP) ，目标是使购买视图的总成本最小化。购买的视图Vp必须满足以下要求：对于查询答案 Q (D)中的元组 t，Vp 中必须存在能产生 t 的视图子集，对于 Q 中的每个关系 R，至少应该购买 R 上的一个视图。对于 Q (D)中不存在的元组 t，Vp 中必须存在一个能表示 t不属于 Q (D)的视图子集。尽管设置中的定价问题通常是 NP-hard的，但 QueryMarket 表明，对于较小的数据集，大量的查询仍然可以在实践中定价。为了处理查询 Q 可能需要来自多个卖家的数据库的情况，他们引入了卖家之间的收入分享策略。具体来说，每个卖方获得查询价格 π (Q)的一部分，这与卖方在 ILP 的所有最低成本解决方案中获得的最大收入成正比。

  Li 等人研究了线性聚合查询的无套利定价模型设计问题。给定一组 n 个实值 x = 〈 x1，. . . . ，xn 〉的数据，对 x 的线性查询是一个实值向量 q = 〈 w1，. . . . . ，wn 〉 ，答案是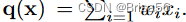

  作者提出了一个市场：数据买家可以购买由买家定义的带有方差约束 v 的单个线性查询 q。查询 Q = (q，v)的回答是 q (x)的无偏估计，方差小于或等于 v。作者首次提出了定价函数 π 的下降速度不能超过1/v 的命题，即
。然后，他们提出了一组无套利定价函数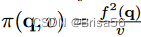
其中函数 f (·)是半范数。最后，他们提供了一个通用框架，用于从现有函数中综合新的无套利定价函数。对于任何无套利定价函数 π1，. . ，πk，如果 f (·)是次加性非降函数，则定价函数 π (Q) = f (π1(Q) ，. . ，πk (Q))也是无套利的。Niu等人列出了一系列著名的无套利定价函数。除了综合定价函数之外，Li 等还研究了一个类似的基于视图的定价框架，就像 Koutis 等所做的那样。通过对文献中的理论结果进行改进，证明了基于视图的线性聚合查询定价模型是 NP-hard的。

  Lin和Kifer研究了一般数据查询的无套利定价。他们提出了三种定价方案：独立于实例的定价、前期相关定价和延迟定价。作者进一步总结了五种套利形式：基于定价的套利，单独的账户套利，后处理套利，偶然套利和几乎肯定的套利。作者指出，Koutris等人的模型，具有基于定价的套利，计算出的价格可能会导致关于D的信息泄露。从理论上讲，他们提出了一个独立于实例的定价函数和一个延迟定价函数，这些函数在所有形式上都是无套利的。。主要的想法是从概率角度来解决定价问题。更有可能显示真实数据库实例的查询的定价更高。

  同样，Deep和Koutris 描述了与信息套利和捆绑套利有关的定价函数的结构，其中信息套利涵盖了Lin和Kifer定义的后处理套利和偶然套利。对于查询的实例独立于定价和依赖于答案的定价，无套利定价函数对于通过询问查询所显示的信息量应该是单调和次附加的。文中给出了无套利定价函数的几个示例，包括加权覆盖函数和香农熵函数。
  Deep和Koutris后来将理论框架实施到实时定价系统QIRANA中，它从不确定性减少的角度计算查询包 Q 的价格。它们假设买方面对的是一组所有可能的数据库实例 S，其模式与真正的数据库实例 D 相同。收到查询答案 E = Q（D） 后，买方可以通过检查 Q（Di） = E 来排除某些数据库实例 Di ∈ S 不可能是 D。消除了越多数据库实例的查询包定价更高，因为它显示了更多关于 D 的信息。他们提出了一个无套利的答案相关定价函数，该函数给每个数据库 Di ∈ S 分配一个权重，并通过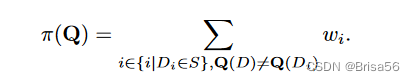
计算查询包的价格。默认情况下，为每个可能的数据库实例 Di 分配相同的权重 wi = P/|S|，其中 P 是数据所有者设置的参数。数据所有者还可以向 QIRANA 提供一些示例查询包及其相应的价格。然后，通过解决熵最大化问题，QIRANA 自动从给定的实例中学习实例权重。选择 S 作为可能的数据库实例的完整集合会导致一个 # P-hard 问题。为了使定价函数易于处理，QIRANA 使用随机抽样的数据库实例作为 S。

  Chawla 等扩展了上图中的定价函数，使卖方收入最大化。他们考虑的设置，供应是无限的，买家是一心一意的，也就是说，一个买家只想购买一个单一的捆绑查询 Q。如果广告中的价格 π (Q)小于或等于买方的估价 vQ，买方将购买 Q。作者采用了一个由一捆查询包和它们的客户价值评估组成的训练数据集。研究了三种定价方案。他们的定价方案的主要思想是，根据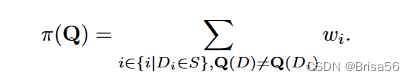
，可以为一捆项目(数据库实例)的查询定价。统一的捆绑包定价，为所有查询捆绑包设置相同的价格。逐一定价使用上图设置查询包的价格，其中权重将从训练数据中学习。XOS 定价学习每个条目 Di 的 k 权重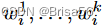
，并将 Q 的价格设为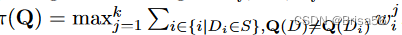
，从理论上研究了各定价方案对最优收益的逼近率。尽管 XOS 定价方案具有最佳逼近率，但实际中逐一定价通常能获得较大的收益。

  Miao 等研究了不完备数据库下的定价选择-投影-自然连接查询问题。基于数据来源的思想，提出了一个无套利定价函数，描述了一段数据的起源及其处理历史。设 t 是查询答案 Q (D)中的元组。T 的谱系 L (t，D)被定义为数据库 D 中对 t 有贡献的元组的集合。作者假设每个元组 t 都有一个基本价格 p (t)。将 Q 的价格设置为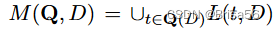
中所有元组成本的加权集合。具体地说，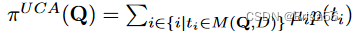
其中 μi 是 ti 的未缺失属性的百分比。作者还提出了一个答案质量感知定价函数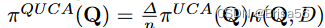
其中 κ (Q，D)是答案质量并且∆是一个常数。然而，π^(QUCA) 并不是无套利的。

  购买数据通常不是一次性交易。客户可以从同一个数据卖方购买多个查询数据。历史感知定价函数不会对已购买过信息的客户收取两次费用。Query-Market会跟踪客户的购买视图，在未来客户再次对这些视图进行查询时避免再次收费。QIRANA和不完整数据库的定价选择-投影-自然连接查询都支持与Query-Market相同的历史感知定价。这些基于历史记录的方法的一个缺点是，卖方必须提供可靠的存储来保留用户的查询历史记录。

  Upadhyaya 等提出了一个最优的历史感知定价函数，也就是说，买家只需为购买的数据支付一次费用。关键的想法是允许买家要求退款已购买的数据。在它们的设置中，查询根据其输出大小定价。卖方为查询答案 Q (D)中的每个元组计算一个标识符(优惠券)。Q (D)和相应的优惠券都发送给买方。如果买方从两个查询中收到相同的元组 t，买方可以通过在两个相应的查询中显示与 t 相关的两个优惠券来要求退款。为了防止购买者从他人那里借取优惠券并获得不合理的退款，每张优惠券都与一个购买者有着独特的联系。通过跟踪优惠券状态，数据卖方保证每张优惠券只使用一次。然而，定价函数没有无套利保证。

3.4.隐私补偿

交易和共享个人数据可能会泄露数据提供商的因此。因此，如何衡量和适当补偿数据提供者的隐私损失是设计个人数据市场的一个重要问题。

  差分隐私是一个严格保障私隐的数学框架。根据差分隐私原理，随机噪音会被注入数据集，使数据购买者可以了解整个数据集的有用信息，但不能准确地了解个人的具体情况。随机噪声的大小影响数据提供者的隐私损失和数据价格。具有较少注入随机噪声的数据集可能泄漏更多的隐私并且定价更高。个人数据的定价模型通常采用成本加成定价策略，卖家首先补偿数据提供商的隐私损失，然后扩大总的隐私补偿，以确定数据购买者的价格。

  Ghosh 和 Roth开始了通过拍卖来定价隐私的研究。他们提议建立一个真实的市场来销售针对二进制数据的单一计数查询。在他们的设置中，数据卖方拥有一个由个人数据 di ∈{0,1}组成的数据集。数据卖方出售一个和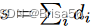
的估计值，并赔偿数据提供者的隐私损失。在差分隐私的框架下，作者将隐私视为一种可以交易的商品。特别是，如果提供者的数据以€-差分私有的方式使用，则应该从提供者购买€-隐私单元。因此，隐私补偿问题可以转化为多单位反向拍卖的变量。作者假设每个数据提供者 i 都有一个隐私成本函数：

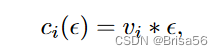
。图中表示以€-差分隐私方式使用数据的成本，其中 vi 是 i 的单位隐私成本。在拍卖中，数据提供者被要求提交他们的要价bi，以便使用他们的数据。Ghosh 和 Roth 考虑两种情况。在第一种情况下，买方对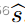
有一个精度要求，即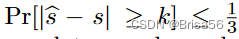
。作者建立了一个观察任务：他们只需要从 m 个人购买数据和使用他们在一个€-差分的隐私方式，其中 m 和只取决于准确性的目标。结果表明，经典的Vickrey-Clarke-Groves拍卖最小化了买方的支付，并保证了拍卖的准确性目标。主要思想是选择 m 个出价最低的个人，并为每个获胜者提供统一的补偿 € · b，其中 b 是第(m + 1)的最小出价。在第二种情况下，买方有一个预算线，并希望最大限度地提高 s 的准确性。作者提出了一种基于贪婪的近似演算法来解决这个问题。

  个人数据的价值和隐私评估可能是相关的。例如，病人可能会给病人的医疗报告定一个比健康人所要求的更高的价格。Ghosh 和 Roth 展示了一个负面的结果，在有这种相关性的情况下，没有任何个体理性的直接机制可以保护隐私。

  在一项后续研究中，Dandekar 等人 考虑了出售线性聚合查询 q = 〈w1， . . . wn〉 超过个人数据 D = 〈d1， . . . ， dn〉 实际值的场景。他们假设数据提供者具有与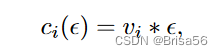
相同的隐私成本函数，并提出了一种真实的逆向拍卖机制，以最大限度地提高预算受限买家的估算器的准确性。真答案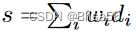
的估计器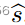
的误差是其平方误差 ( ^s − s）^2。 结果表明，从q中具有较大相应权重的更多提供者计算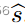
更准确。因此，问题被转化为背包逆向拍卖[95]，在预算限制下最大化所选提供商的总权重。具体而言，作者将预算视为背包的容量，将数据输入di的隐私成本视为其在背包中的权重，wi视为di的值。针对该问题，提出一种逼近比率为5的基于贪婪的算法。

  上述研究[34,19]假设数据购买者可以从每个数据提供者购买任意数量的隐私。然而，如果隐私损失太大，保守的个人可能不想出售个人的数据。Nget 等[77]研究了与 Dandekar 等[19]在更现实的情况下所做的相同的问题，即如果 i 的隐私损失大于阈值 i，那么个体 i 可以拒绝参与估计。他们假设每个数据提供者的隐私成本函数是公开的，并提出了一种启发式的查询价格确定方法。模型首先随机抽样一部分数据提供者。然后，以 i 差分私有方式使用每个采样个体 i 的数据，并相应地计算补偿。如果总报酬大于预算，模型会降低高成本供应商的差分隐私水平，从而达到预算目标。最后，他们通过个性化的差分隐私生成受干扰的查询答案，这保证了每个被选中的个体的差分隐私。他们重复上述步骤多次，并返回最小的平方误差的扰动答案。

  后来，Zhang等[111]提出了一个真实的个人数据市场，在这里每个数据提供商可以指定个人最大可容忍的隐私损失 i。他们首先表明，查询答案的准确性与购买隐私的总金额成正比。在假设所有个人的隐私成本分布是公开的情况下，他们设计了贝叶斯最优背包采购的变体[29] ，其在数据买家的预期预算的约束下最大化预期购买的总隐私。作者通过采用文[29]中的算法来解决这个问题。嘈杂的查询答案是使用个性化差分隐私生成的[50] ，这保证了每个选定的个体 i 的 i-微分私密性。

  Dandekar 等[19]、 Ghosh 和 Roth [34]提出的模型可能受到套利的攻击。Li 等[57]考虑这样一种情况，数据购买者对所购买的嘈杂的查询答案具有方差约束 v。他们假设个人的隐私成本是公开的，并提出了一个将无套利价格分配给线性聚合查询 q 的理论框架。通过将拉普拉斯噪声与期望值0和方差√(v/2)相加，从真实的答案中得到一个不确定的答案。用差分隐私来衡量，如果个人参与查询，个人 i 的隐私损失上界为 €= w/( √(v/2))，否则为0，其中 w 是 q 中最大的绝对权重。提出了几个隐私补偿函数，如 pi (€) = ci·€i，其中 ci 是个人 i 的单位隐私成本。查询的价格是隐私补偿的总和，这被证明是无套利的。

  Li 等人[57]只对参与查询的个人进行补偿。然而，由于两个人的数据可能是相关的，一个没有参与出售的个人的隐私可能会因为另一个人的数据被泄露而被泄露。为了公平地补偿个人的隐私，Niu等人[78]扩展了Li等人[57]的模型，并提出了一个无套利和依赖公平的定价模型。依赖公平性要求数据提供者只要在查询中涉及到与该提供者的数据相关的其他提供者的某些数据，就应该得到隐私补偿。使用依赖差分隐私[60] ，数据提供者 i 由查询引起的隐私损失上限为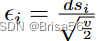
。其中 dsi 是查询对提供者 i 的数据的依赖敏感度。作者提出了一种自底向上和自顶向下的机制来确定隐私补偿和查询价格。自底向上机制以与 Li 等人相同的方式计算补偿，并将查询价格确定为总补偿的倍数。自顶向下机制首先使用用户定义的无套利定价函数确定查询价格，并将买方支付的一部分用于隐私补偿。每个数据提供者都会得到与其隐私损失成比例的补偿分成。

  上面讨论的所有隐私补偿方法都假设有一个值得信赖的平台/代理来与数据购买者交易数据提供者的隐私。但是，数据提供程序不能控制自己数据的使用。

  在这方面，Jin 等人开发了一个真实的群体感应市场，在这里数据所有者可以决定披露多少隐私。在他们的市场，模糊了地理位置的数据所有者是通过拍卖交易。数据所有者首先根据他们自己的隐私偏好向他们的数据注入随机噪音。然后，每个数据所有者用注入的随机噪声的均值和方差以及费用进行投标。买方决定拍卖中标者，以最大限度地提高有关买方预算线的数据准确性。作者指出，这个最佳化问题是 NP-hard的，并提出了一个贪婪的启发式解决方案。主要的想法是迭代地选择数据所有者，使最大的边际效用贡献，直到预算用完。

  在这一部分中，我们回顾了在四种情景下的原始数据集的代表性定价模型，其中考虑了不同的需求。讨论的定价模型的一个局限性是，数据集的定价没有考虑它们的下游应用。Fernandez 等[30]认为，数据集对客户的价值通常是依赖于任务的，不能仅仅通过数据集的内在属性来评估。由于原始数据集的定价模型与原始数据集的下游应用无关，因此这些定价模型可用于建立受监督模型和非监督式学习模型的机器学习过程中。

4.定价数据标签

众包是机器学习任务中收集大规模标记训练数据的一种流行方法[88]。不幸的是，众包数据往往存在质量问题。这主要是由于参与者可能会提交低质量的标签。可以通过以绩效为基础的报酬来阻止他们参与这些任务。然而，由于标签收集缺乏地面真实性验证，如何评价标签的质量和价格相应的标签是一个具有挑战性的任务。在本节中，我们回顾了两种类型的标签定价模型，这些模型旨在激励工人努力工作并提交准确的数据标签。

4.1.黄金任务定价模型

  黄金任务是数据购买者事先知道答案的任务。黄金任务可以在工人评价工人表现的任务中均匀地随机混合，这决定了工人的报酬。由于工人无法区分黄金任务与其他任务，这种策略可以激励工人提供准确的标签。

  Shah和Zhou[88]考虑一个众包设置，工人执行二进制标签任务。作者提出了 一种使用gold任务的乘法定价模型。如果工作人员不确定答案，则该模型允许工作人员跳过分配的任务。对工人u的总付款是根据u在回答的任务上的表现来计算的。工人是自私的，并希望最大限度地提高他们个人的预期付款。 作者假设每个工人都有一个关于任务t的真实标签yt是l的可能性的个人确信度Pr （yt=l）。定价模型旨在激励工人只报告确信度大于阈值p的高置信度标签。总奖励从β开始，对于黄金任务中的每个正确答案，奖励将乘以1/p。然而，如果这些黄金任务中的任何一个答错了，奖励就会降为零，也就是说，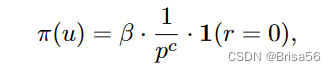
(5)
其中1(·)是一个指示函数，c 和 r 分别是正确答案和错误答案的数量。这种定价模式激励员工只回答他们有足够信心的任务。定价模型是激励相容的，也就是说，当且仅当工人努力报告准确的标签时，工人才能得到最大的预期报酬。这种定价模式也满足了“没有免费午餐”的公理，也就是说，只提供错误答案的员工将得不到任何报酬。在他们的设置中，提出的方法是唯一的激励相容模型，满足“不免费午餐”公理。

  Shah 等人[90]进一步将Shah和Zhou的模型[88]推广到多标签任务。对于每个任务，工作人员可以提交多个他认为最有可能是正确的答案 Y。这种多重选择系统为工人表达自己的信念提供了更大的灵活性，可以比单一选择系统更有效地利用具有部分知识的工人的专业知识。作者假设工人对每个标签都是任务的真正标签的确信度在集合{0} ∪（p，1]中，其中p是固定的和已知的。作者希望鼓励员工只报告带有强确信度的标签集。如果一个工作者的一个答案是正确的，那么这个工作者完成一个黄金任务的奖励是(1-p)^(|Y|-1) ，否则是0。支付给工人的总金额取决于工人对所有黄金任务的奖励产品。

  在后来的研究中，Shah 和 Zhou [89]提出了一个两阶段乘法定价模型，以激励员工自我纠正他们的答案。在第一个阶段，工作人员回答分配的任务。在第二阶段，如果工作者对任务 t 的回答与同行工作者的回答不一致，工作者有机会改变答案。如果任务的初始答案是正确的，那么工人 u 将获得高额奖励，如果更新后的答案是正确的，那么工人 u 将获得低额奖励，如果最终答案是错误的，工人 u 将获得0额奖励。总的报酬是由工人从黄金任务中获得的报酬的产品决定的。从理论上证明了该方法是唯一满足非自由发布公理的激励相容模型。经验表明，与标准的单级设置相比，自校正设置可以显著提高数据质量。

  为了减少收益的差异，上述方法[89,90,88]要求每个工人解决足够数量的黄金任务。这将导致采购预算的浪费，因为黄金任务的答案已经为人所知。

  De Alfaro 等[2]通过结合同伴预测和黄金任务的思想来解决这个问题。他们将工人安排在一个层次结构中，每个工人与其每个子级分享一个共同的任务。一些黄金任务被用来激励高层工作人员的高度努力。假设这些工作者付出了足够的努力来提供高质量的答案，他们的答案可以作为第二层工作者的伪黄金任务，而第二层工作者又可以为下一层提供伪黄金任务，等等。如果工人不同意上一层分担的任务，工人将受到惩罚。由于顶层工作人员是通过真正的黄金任务来评价的，因此他们比其他工作人员得到的评价更准确，这对低层工作人员是不公平的。

  Goel和Faltings的后续工作考虑了工人之间的公平报酬，也就是说，工人的预期报酬与工人回答的准确性直接成比例，与工人的随机同伴的策略和熟练程度无关。其核心思想是评估工人的熟练程度，即工人正确解决任务的概率。Goel和Faltings[36]首先估计一小群工人的熟练程度与黄金任务。然后，小组工人对非黄金任务的回答被用作贡献的黄金任务，其中工人的熟练程度被用作这些任务的可信度。贡献的黄金任务被用来评估更多工人的熟练程度。最后，每个工人的报酬与工人的估计熟练程度成正比，因此熟练程度高的工人会得到高额报酬。这种模式保证，尽最大努力提供准确的标签是每个工人的主导战略。

4.2.基于同行预测的定价模型

基于同行预测的定价模型可以激励工作和准确的数据标签，而无需访问黄金任务。这些模型利用同一任务答案的随机相关性，在工人之间建立了一个博弈，在博弈论中称之为机制。这个游戏的设计使得努力解决任务的工作者可以获得高预期的回报，而垃圾邮件发送者提供随机答案平均没有收到任何报酬。一个定价模型是激励相容的，如果它承认作为一个均衡发挥高度的努力和真实的报告。

  Dasgupta 和 Ghosh [20]发起了努力启发的研究，并提出了 DG 模型来定价二进制标签。数据购买者将一组数据标记任务分配给一组工作者，这样每个任务都由多个工作者标记，每个工作者标记多个任务。它们假设一个工人 ui 要么不投入任何努力，因此提供一个随机标签，要么投入全部努力创建一个具有成本 ci 的标签，并提供一个具有概率 π 的真实标签。在这里，π 被称为 ui 的熟练程度。工人们都是利己主义者，他们想要最大化他们的回报。
  DG 模型根据工人 ui 的报告与对等工作者的报告惊人的一致程度，为分配的任务 t 支付一个工作者 ui。分别用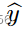
和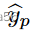
表示 ui 和 up 到任务的答案。该模型支付 ui 一个固定的报酬，减去概率 Pr(ui，up) ，ui 和 up 对随机任务有相同的答案，也就是说，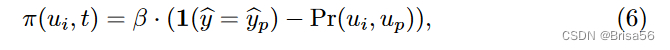
其中 β 是一个非负的支付比例参数，被选择来覆盖工人的努力成本，而 Pr(ui，up)是从提交的标签中近似得到的。支付给工人 ui 的总金额是 ui 为每个任务支付的总金额。
  这种定价模式鼓励人们付出努力，因为对于那些没有解决他们的任务并报告随机/恒定标签的垃圾邮件发送者，他们的预期报酬是零。在所有员工的熟练程度都优于随机猜测的假设下，证明了 DG 模型是激励相容的。尽管定价模型也存在非信息均衡(例如所有员工报告的标签相同) ，但这些均衡对员工的利润较低，因此对员工没有吸引力。

  在多标签的情况下，两个标签 l1和 l2可能是正相关的。Shnayder 等[92]表明，在 DG 模型下，工人可以通过误报11/12来获得更多的利润。相关协议(CA)机制[92]将 DG 模型扩展到多标签任务。在 CA 机制中，需要有关标签相关性的知识。一个标签相关矩阵⊿是从工人提交的文件中学习到的，其中一个元素 ⊿i，j = Pr (li，lj)-Pr(li)·Pr(lj)是标签 li 和 lj 之间的相关度。用 S (·)表示⊿的符号函数，也就是说，如果⊿i，j >则S (li，lj) = 1，否则为0。如果你的报告与同事的报告呈正相关，那么你的工作就会得到奖励。为了惩罚所有工人盲目报告相同标签的情况，如果工人在随机任务中可能与工人保持一致，那么工人将受到惩罚。特别是，向工人 u 报告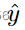

的付款是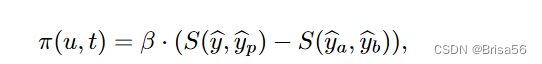
其中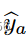
是工人 up给出的任务t的答案。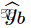
是工人u对随机任务的答案，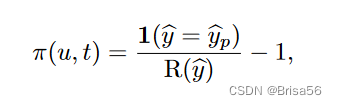
是工人up 对另一个随机任务的回答。
当任务数量较大时，能够准确地学习标签相关性⊿，CA 机制是与最高报酬相容的激励机制。然而，如果两个标签 l1和 l2对 S (·)不可区分，即 ∀li∈Y，S(l1，li)=S(l2，li)则该机制失效。在这种情况下，工人可能误报 l1，l2，但仍然得到相同的报酬。

  Radanovic 等[82]对多标签任务的定价提供了补充的理论结果。他们假设标签只有有限的相关性，即 Pr(op=l2 | o=l1) < Pr(op=l2 | o=l2) ，其中 o 和 op 分别是工人 u 和 工人up 的观察标签。该机制支付报告 y 由工人 u 在一个任务 t 由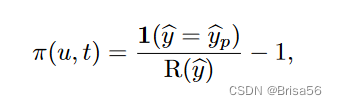
其中 R(^y)是 y 的经验频率，这是从所有提交的计算。结果表明，高度的努力和真实的报道比任何其他均衡都更有利可图。然而，他们关于标签相关性的假设在某些应用中可能不成立[92]。

  上述方法[20,92,82]要求每个任务必须由至少两个工作人员完成，这导致重复的答案，因此不能有效地利用群体。对于二进制标签的设置，Liu 和 Chen [62]建议从工人报告中学习分类器 M，并使用分类器的预测 M (t)作为同行报告。由于工人提交的标签是高噪音的，因此分类器会接受高噪音标签学习技巧的训练[75]。具体来说，他们首先估计提交标签的错误率。然后，利用 Natarajan 等[75]提出的误码率校正损失函数 φ (·)对分类器进行优化。任务 t 的报告 y 的定价基于 -φ (M (t) ，y) ，这样损失大的标签的定价较低。在 M 优于随机猜测的假设下，努力寻找真理标签是最高收益的均衡。
  Liu和Chen[63]研究了序贯标签收集问题，其中标签任务分多个阶段发布。在他们的设置中，一个精确标记的任务对数据购买者有固定的奖励，而一个错误标记的任务对数据购买者没有价值。他们提出了一个激励相容的定价模型，使数据购买者的期望效用最大化，即总报酬和总支付之间的差额。
  他们开发了一个多臂老虎机算法来扩展 DG 模型[20] ，该模型动态调整
中的参数 β。更大的 β 可以鼓励更准确的标签，但是要花更多的钱。由于盗贼算法需要一个静态的环境，如果对手工作者根据他们与机制的相互作用调整策略，这种方法可能无法学习最佳的 β [42,37]。Hu等人[42]通过强化学习来解决问题，这对工人的战略行为更有效。

  在实践中，基于同行预测的模型需要调整付款以避免负付款。这种调整可能会导致垃圾邮件发送者可能会获得积极和高额的奖励。Radanovic和Faltings[81]通过提出一个声誉系统PropeRBoost来调整付款来解决这个问题。PropeRBoost 在多个轮次中向工作人员发布任务，并根据工作人员过去提交的文件计算每个工作人员的声誉分数。在每个回合r中，它首先应用DG模型[20]来计算工人的付款，然后根据相应工人的声誉重新扩展付款。结果表明，当r接近无穷大时，垃圾邮件发送者的平均付款收敛到0。

  在本节中，我们将介绍数据标签的基于黄金任务和基于对等预测的定价模型。开发的定价模型保证了努力报告准确的数据标签是所有工人最有利可图的策略。基于黄金任务的方法的一个主要问题是，这些方法需要足够数量的黄金任务才能获得良好的性能。但是，在某些情况下，获取黄金任务的成本非常高。对于基于同伴预测的方法，多重均衡的存在是一个主要限制，因为工人可能会收敛到一个没有信息的均衡，工人没有全力[93]。

5.机器学习模型协同训练中的定价

协作式机器学习是一种吸引人的范例，其中多个数据所有者通过贡献其数据来协作构建高质量的机器学习模型。由于来自不同数据所有者的数据集可能对训练的机器学习模型有不同的贡献，因此贡献更多有价值数据的数据所有者应该获得更多奖励[94]。在本节中，我们将回顾协作机器学习中的贡献评估和收入分配技术。

5.1.根据Shapley值分配收入

Shapley公平被广泛采用为协作机器学习中公平收入分配的基础。它保证每个参与者收到的付款与参与者对训练的机器学习模型性能的边际贡献成比例。采用沙普利价值的挑战在于其指数计算成本。

  Maleki等人[67]通过提出有界效用函数的排列抽样算法来解决Shapley值的效率问题。根据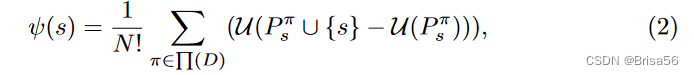
，卖方的Shapley值是所有可能的卖方子集的边际效用贡献平均值，可以通过样本均值来估计。用卖方 Shapley 值的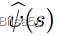
和（€， δ）近似值表示，即[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iGodx5W4-1677805115728)(images/756cfab1c9a6dd20c9f24455571173b8d18776f6cbb3d4875f5c860285620741.png)] 为了计算所有卖者的估计量，通过Hoeffding不等式[40]，我们需要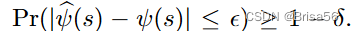
样本并计算效用函数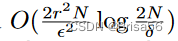

，其中N是卖方的数量，r是效用函数的范围。评估效用函数本身，例如计算测试准确性，计算成本很高，因为它需要训练机器学习模型。因此，该方法无法扩展到大量卖家。

  Ghorbani和Zou [33]扩展了Maleki等人的蒙特卡洛方法[67]，以在监督学习中对单个数据点进行定价，并提出了截断基和基于梯度的近似方法。他们基于截断的方法通过忽略大型联盟来减少效用评估的数量。作者认为，将Shapley值估计为测试数据集上预测性能U中的固有噪声就足够了，这可以作为U的自举方差来测量。此外，通过向大型训练数据集 S 再添加一个训练数据点 s 而导致的性能变化可忽略不计。因此，如果 S 的效用接近整个数据集 D 的效用，则 s 对 S 的边际贡献在实践中可以被视为 0，因此其计算可以被截断。他们基于梯度的方法通过减少训练时间加快了效用函数的评估，其中模型只需通过训练数据进行一次训练即可。他们通过一次对一个数据点s执行梯度下降来更新模型，s的边际贡献是模型性能的变化。这两种近似方法在近似的Shapley值中引入了估计偏差，并且不能保证近似误差。

  Jia等人[46]提出了两种近似算法，其中 Shapley 值具有可证明的误差界，显著减少了效用评估的数量。第一种算法在特征选择中采用了分组测试的思想[114]。用 βi 表示一个布尔随机变量，用于表示卖方 si 是否在卖方的随机样本中。Β1，. . ，βN 的抽样分布被设计成卖方 si 和卖方 sj 之间的 Shapley 值差为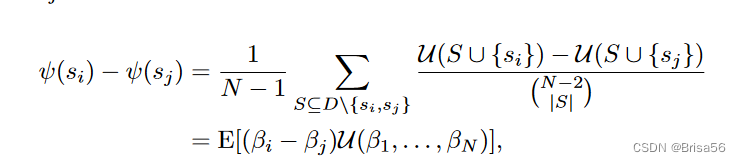

其中U（β1， . . ， βN） 是出现了的卖家的评估的效用，D是所有卖家。卖方的 Shapley 值可以通过求解可行性问题，从所有数据对之间的估计 Shapley 差异中推导出来。它们证明该算法返回具有 O(N(logN)^2)效用求值的（€， δ）近似值。第二种算法基于他们的观察，即 Shapley 值近似稀疏，也就是说，大多数值都围绕平均值。利用这一特性，他们将稀疏信号恢复的思想应用于压缩传感[83]，并开发了一种算法，该算法仅通过O(N(logN))实用程序评估产生（€， δ）近似值。
  Jia等人[45]进一步发现，在未加权的kNN分类器中使用的数据点的Shapley值只能在O（NlogN）时间内精确计算。给定一个带有标签 ytest 的测试点 xtest，他们将 kNN 分类器的效用定义为 ytest 的可能性，即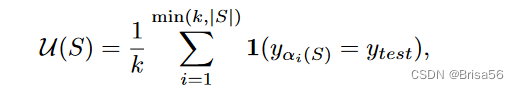
其中 αi（S）是训练数据的索引，它是数据点 S 集中最接近 xtest 的第 i 个索引。特殊效用函数可以高效计算两个数据点 xαi（S） 和 xαi+1（S） 之间的Shapley差值，即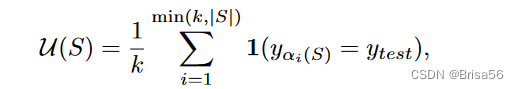
。他们首先计算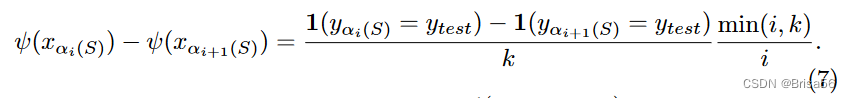
，然后利用等式 7 以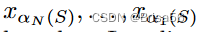
的顺序递归计算 Shapley 值。他们进一步开发了一种基于局部敏感哈希[21]的（，δ）近似算法，仅具有亚线性复杂性。主要思想是只计算检索到的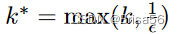
最接近 xtest 的邻居的 Shapley 值，而忽略其余数据点，因为它们的 Shapley 值太小。此外，他们提出了一种具有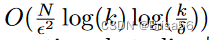
时间复杂度的蒙特卡罗近似算法， 用于加权kNN分类器。

  上述研究[45,46,33]通过模型在验证数据集上的表现来评估模型的效用。Sim 等[94]考虑了没有可用的验证数据集的情况，并建议使用模型参数的信息增益作为效用函数。用 θ 表示模型参数。对数据 D 进行训练后，信息增益 IG(θ) = H(θ)-H(θ|D)是 θ 不确定性的降低，其中 H (·)是熵函数。除了Sharply公平外，还提出了收入分配的三个附加激励条件，即个人理性、大联盟的稳定性和群体福利。他们还提出了 p-Shapley 公平性，即给卖方 si 分配一个奖励 π(si) = kψ(si)^p。通过调整参数 p ∈[0,1] ，它们可以在实现不同的激励条件之间进行折中。每个参与者都会得到一个机器学习模型作为奖励，而不是金钱奖励。为了实现不同级别的奖励，模型通过在训练标签中注入不同级别的噪声进行训练。

  联合学习[7,68]使多个分散的参与者能够协作训练一个机器学习模型，同时将他们的训练数据保持在本地。参与者提供的数据集按照中央服务器确定的顺序使用。使用 Shapley 值评估参与者的贡献会在分散的参与者之间产生很高的沟通成本。此外，Shapley 值忽略了数据源的顺序。为了适应这些挑战，Wang 等[103]提出了联合 Shapley 值。用 U (si + sj)表示该模型的实用性，该模型首先对 si 的数据进行训练，然后对 sj 的数据进行训练。设它是联邦学习过程中的一组被选中的参与者。参与者 si 在第 t 轮的联合 Shapley 值定义如下。

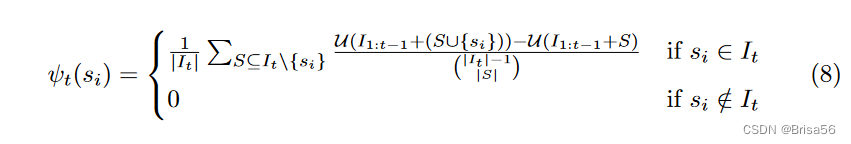
si的联合Shapley 值是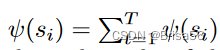
其中 T 是联邦学习中的总回合数。作者表明，联合Sharply值满足Sharply公平的平衡和加法公理。另外两个公理，对称性和零元素，在每一轮中都得到满足。他们扩展了排列抽样和组测试近似方法[46]来计算联合Shapley值。

  联邦学习的参与者花费一些成本来贡献他们的数据集，例如隐私成本[41]和能源成本[51]。Yu等人[108]提出了一种公平的联邦学习收入分配机制，该机制共同考虑了参与者的成本和贡献。在回合 t 中，每个参与者 si 都有一个公共成本 ci（t）并获得奖励 πi（t）。si 的后悔 ri（t） 是 si 的总成本和总回报之间之差的函数。ri（t）的大值表明si没有很好地补偿si产生的成本。笔者认为，每轮参与者的支付应达到贡献公平和后悔公平。贡献公平性要求每个参与者的支付πi（t）和Shapley值ψt（si）应正相关，即∑i πi（t）ψt（si）应最大化。后悔公平性要求参与者应该有相似的遗憾，即参与者之间后悔的差异应该最小化。参与者的付款是通过解决与预算约束相关的优化问题来确定的。从理论上讲，他们表明参与者的时间平均后悔是t→ ∞常量值的上限。

  Shapley 值容易受到数据复制攻击。数据提供者可以零成本复制他/她的数据，并充当额外的提供者，以获得额外的不合情理的奖励。Agarwal等人[1]通过惩罚类似的数据集来抑制复制来解决这个问题，也就是说，复制稳健的Shapley值被定义为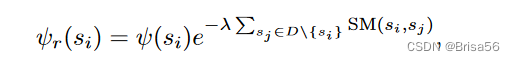
其中 SM 是相似性度量，λ 是常量。然而，所提出的复制稳健的Shapley值不再满足沙普利公平中的平衡公理。

  Han等人[38]研究了具有子模块效用函数的数据市场中的复制攻击。它们表明，攻击者获得的总奖励相对于攻击者的复制次数单调增加。他们发现，对攻击者的额外奖励主要来自攻击者的复制对小卖家群体的边际贡献。为了解决这个问题，作者建议在计算Shapley值时降低这些贡献。他们的方法保证了攻击者通过更多的复制获得更小的奖励。

  Ohrimenko等人[79]设计了一个复制健壮的协作数据市场，要求每个参与者支付参与费。此方法不鼓励复制，因为攻击者收到的额外奖励无法覆盖攻击者的参与成本。

5.2.其他收入分配方法

除了Shapley价值之外，协作机器学习中还有其他一些收入分配方法。

  Leave-one-out [18] 是评估数据重要性的常用方法。它将在完整数据集上训练的模型的性能与在完整数据集上训练的性能减去一个点进行比较。性能下降定义为数据点的值，即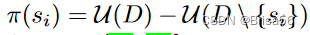
Leave-one-out通常由影响函数 [18， 52] 近似，该函数测量模型如何随着训练点的权重更改而变化，而无需重新训练模型。Richardson等人[85]应用影响函数来奖励联邦学习的参与者贡献的数据点。结果表明，定价模型是激励兼容的。[84， 46] 中还研究了将影响函数应用于价格数据点。与 Shapley 值相比，一般而言，留一出方法效率更高，因为它们不需要模型重新训练。但是，遗漏方法可能无法准确评估数据点的值。无论基准面有多重要，这些方法都可能为两个完全等效的数据点之一分配一个较低的值，因为通过包含另一个基准面仍然可以实现高性能[106]。

  Yan和Procaccia [104]设计了一个基于核心[35]的数据定价模型，这是合作博弈论中著名的收入分配解决方案。该解决方案旨在实现参与者如何相互协作的最大稳定性。核心要求每个联盟 S 的总奖励应至少等于效用 U（S），即 ∀S ⊆ D，∑ si∈S π（si） ≥ U （S），其中 π（si） 是参与者 si 的奖励，D 是所有参与者的集合。当无法实现这样的奖励时，最小核心通过允许S的效用与S的总奖励之间的最小差异来放松约束。特别是，最小核心通过求解以下线性程序来计算对每个参与者的付款。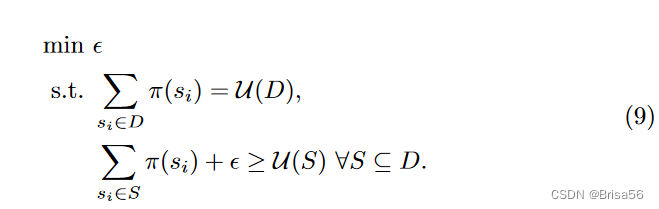
等式9中的约束数量相对于参与者数量呈指数级增长。Yan和Procaccia [104]通过提出一种具有保证近似误差的蒙特卡罗近似算法来解决效率问题。他们的近似方法对相对较少的联盟进行采样，并求解采样联盟上的等式9。如果等式9有多个解，则选择具有最小l2范数的解。他们的收入分配满足了沙普利公平的平衡、对称和零元素公理。

  Yoon等人[106]提出了一种强化学习算法来评估数据点的价值。他们学习一个数据值估计器，该估计器估计数据值并选择最有价值的样本来训练目标分类器。它们共同学习数据值估计器和相应的分类器，这使得分类器和数据值估计器能够相互提高性能。但是，这种方法不能保证参与者之间的收入分配公平。

  大多数现有的收入分配方法是在监督机器学习模型联合训练的设置中开发的。参与者将根据其数据集对联合训练的机器学习模型的实用性的贡献获得奖励。为了使现有的定价模型适应联合训练无监督机器学习模型的场景，主要的挑战是开发一个参与者都能同意的效用函数。对于一些传统的无监督机器学习模型，有一些被广泛接受的性能指标可以作为效用函数。例如，Silhouette Coefficient(剪影系数) [86] 和Calinski-Harabasz index(卡林斯基-哈拉巴斯指数) [12] 被广泛用于评估地面实剖分类未知时聚类算法的性能。然而，为一些无监督模型开发效用函数，例如预先训练的深度语言模型[26，9]，可能具有挑战性，因为它们在许多下游机器学习任务中的评估方式不同。

  在本节中，我们将回顾机器学习模型的协作训练中的定价模型。主要思想是根据每个参与者的数据集对联合训练的机器学习模型的性能的贡献来定价。Shapley基于价值的方法保证了参与者之间的公平收入分配，但计算效率和可扩展性较差。一些替代方法[106，104]享有更好的效率或联盟稳定性，但失去了公平性的保证。

6.定价机器学习模型

许多不同的应用程序和方案都需要机器学习模型。许多用户和公司没有从头开始构建机器学习模型，而是由于缺乏专业知识和计算资源而转向购买训练有素的机器学习模型[109，16]。在本节中，我们将回顾机器学习模型的定价模型，并讨论机器学习模型和原始数据集之间的定价差异。

6.1.定价模型

机器学习模型定价是一个新兴的研究领域。据我们所知，现有的研究主要集中在无套利和收入最大化定价上。

  Chen等人[16]提出了一个无套利和收入最大化的机器学习模型市场。在他们的环境中，模型所有者向不同的买家出售机器学习模型的多个版本。卖方首先在整个原始数据集上训练最佳模型。然后，卖方通过在最优模型的参数中添加具有不同方差的高斯噪声来生成不同版本的最优模型。生成的模型实例的预期错误率相对于注入噪声的方差单调增加。无套利定价功能可保证买方无法通过支付更少的费用来获得高性能模型。在他们的机制下，定价函数是无套利的，当且仅当该函数相对于噪声方差的逆向是单调和亚加性的。不幸的是，他们的定价模型仅适用于使用严格凸目标函数训练的机器学习模型。
  Chen等人[16]进一步研究了机器学习模型定价中的收入最大化，这些模型与一组买家的需求和估值有关。他们表明，确定最佳价格是coNP-hard的。为了克服计算硬度，他们通过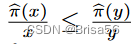
放宽附加约束π(x+y) ≤ π(x)+π(y)
，其中 x ≤ y 和 ̂ π 是最优定价函数π的近似值。它们表明 ̂ π 是无套利的，并且∀x>0，π(x)/2 ≤ ̂ π（x） ≤ π（x）。他们提出了一种动态规划算法，用于在O（n^2）时间内计算̂ π，其中n是模型版本的数量。

  Liu等人[61]提出了一个端到端的模型市场，它共同考虑了数据所有者的隐私成本和模型购买者的需求。经纪人从数据所有者那里收集数据，并生成机器学习模型的多个版本进行销售，其中包含不同的训练数据子集和不同的隐私级别。收入完全分配给数据所有者。客观扰动[14]用于训练具有所需微分隐私水平的模型，从而将量化的随机噪声注入模型的目标函数中。每个数据所有者都要求使用所有者的数据来训练具有 €-差异隐私的模型的最低补偿，即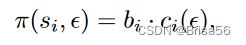
其中 bi 与 si 相对于所有卖方数据集的 Shapley 值成正比，ci（€） 是 si 的隐私成本。理想的定价模型应保证收入最大化，在不同的隐私级别方面无套利，并涵盖对数据所有者的补偿。计算最优定价函数是coNP-hard的，因此他们提出了一种动态规划算法来近似地解决问题。定价模型的局限性在于它无法根据动态客户需求调整价格，这可能会限制经纪人的收入。

  Agarwal等人[1]考虑对机器学习模型市场进行在线拍卖，这是真实的，收入最大化。他们假设买家一次来一个，每个人都想为买家的预测任务购买一个机器学习模型。用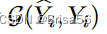
表示模型的预测质量 ̂ Yi 对买方 i 的验证数据集 Yi。我从模型中获得的买方奖励是μi ·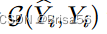
，其中μi是买方i对单位业绩的私人估值。分别用 pi 和 bi 表示经纪人的要价和买方 i 的出价，表示单位性能。经纪人根据价格差异 pi − bi 为买方 i 生成一个嘈杂的机器学习模型。具体而言，模型在具有量化注入随机噪声的数据集上进行训练，使得模型的性能按比例降级为 pi − bi。买方 i 由函数 RF（pi、bi、Yi）收取费用，该函数是按照Myerson的支付函数规则 [71] 设计的。买方我通过投标bi收到的效用是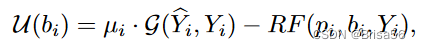
其中 ̂ Yi 是返回的噪声模型的预测。结果表明，如实出价买方的估值μi可以最大限度地提高买方i的效用。作者应用乘法权重方法[3]从历史收入中计算价格pi。他们表明，定价机制实现了最大的收入。

6.2.原始数据产品与机器学习模型的定价

在高层次上，机器学习模型和原始数据集的定价共享一系列常见的需求和技术。但他们的定价模式至少在四个方面存在本质差异。

  第一，机器学习模型的定价单位通常是明确定义和固定的。机器学习模型通常作为一个整体定价和销售。客户可以通过 API 调用购买机器学习模型或使用机器学习模型，其中每个调用都有固定的价格。相比之下，原始数据集可以以多种粒度使用。例如，客户可能对去年美国客户的销售信息感兴趣。但是，另一位客户可能希望在圣诞节期间购买销售信息。这种灵活性使得原始数据产品的版本更容易，并实现了更灵活的定价机制。例如，根据显示的信息量，可以将不同的价格分配给同一数据库上的不同查询[25]。

  其次，模型市场中的版本控制比数据市场中的版本控制更难。由于数据集具有强大而灵活的聚合性，因此可以通过按不同维度聚合来轻松生成数据集的不同版本。生成不同版本的机器学习模型需要更复杂的技术[16]，因为准确控制多个版本之间的差异具有挑战性。

  第三，原始数据集对客户的价值通常比机器学习模型更难衡量。通常，原始数据集用于训练机器学习模型。数据集的最终价值不仅取决于其内在属性，还取决于数据集用于的特定任务和分析方法[30]。因此，客户通常很难理解数据集的价值。许多机器学习模型是为特定任务而设计的，并被人们直接用于支持决策[1]。人们更容易验证和理解这种机器学习模型的价值。例如，客户可以根据分类模型的预测准确性来评估分类模型。

  最后，在模型市场中，防止套利通常比在原始数据市场更难。正如 Tram’er 等人 [100]、Yu 等人 [109] 所表明的那样，机器学习模型可能被攻击者通过合理数量的 API 调用窃取。具有大量查询实例的客户可能会首先从目标机器学习模型购买一些预测。然后，客户可以使用接近等效的输出作为目标模型来训练本地模型，并使用本地模型来预测剩余的查询实例，几乎不需要任何成本。

  在本节中，我们将回顾机器学习模型的定价。我们首先重新审视无套利和收入最大化定价模型。然后，我们将讨论机器学习模型产品和原始数据集产品之间的几个主要区别，包括定价单位、版本控制、套利预防和客户估值。

7.结论和未来方向

在本文中，我们调查了端到端机器学习管道中的数据定价。我们考虑了机器学习管道中可能涉及定价的三个重要步骤，即原始数据收集和标签，协作训练机器学习模型和机器学习模型市场。我们系统地回顾了这些步骤中的代表性研究，讨论了定价原则并审查了现有方法。端到端机器学习管道在当前的大数据和人工智能经济时代扮演着越来越重要的角色。据我们所知，这是关于机器学习管道中数据定价的首次调查。

  数据定价仍处于早期阶段。未来的工作面临许多研究挑战。我们在这里列出了其中的一些。

  首先，现有的研究集中在机器学习管道的每个单独阶段设计适当的奖励模型。缺乏对端到端收入分配解决方案的系统研究。正如我们在调查中介绍的那样，机器学习模型的制造过程涉及多方，包括数据所有者，数据处理者，机器学习模型设计人员和其他可能的参与者。每一方在管道的一个阶段提供增值贡献并获得奖励。一个自然的问题是如何在各方之间分配制造预算。为了回答这个问题，我们需要一种机制来衡量和比较不同组织在不同阶段的贡献。我们还需要一个能够根据供需变化动态调整预算分配的系统。

  其次，几乎所有协同模型训练的定价模型都将收入分配作为合作博弈来制定，并利用Shapley价值进行分配。他们通过四个公理来证明Shapley值的使用是合理的，即平衡，对称，零元素和可加性。然而，Yan和Procaccia[104]认为，数据估值的可加性的必要性是值得商榷的。除了可加性公理之外，合作博弈论中许多其他著名的分配也可以满足其他三个公理。与Shapley价值相比，其他解决方案有其优点和局限性。例如，标准化的Banzhaf值[13]计算每个玩家的付款作为玩家对其他玩家的所有联盟的平均边际贡献。尽管归一化Banzhaf值不满足加性公理，但它对数据复制攻击的鲁棒性比Shapley值[38]更可靠。在稳健性比可加性更重要的市场中，标准化的Banzhaf值比Sharply值更可取。不同类型的数据市场可能有不同的目标[30]，因此需要不同的公理。因此，我们需要更好地了解不同市场中的必要公理，并探索特定市场的收入分配解决方案。

  第三，机器学习任务的细粒度数据获取没有得到充分探索。在实践中，来自两个卖家的数据集可能具有相似或重叠的部分。预算有限的数据购买者可能不想购买过多类似的数据点，因为训练数据集的多样性对于机器学习模型的性能至关重要[30]。基于查询的定价模型[53]允许数据购买者仅购买数据集中感兴趣的部分。但是，现有的基于查询的定价模型仅针对垄断市场中的关系数据集而设计。在与竞争卖家的通用数据集市场中支持基于查询的定价带来了新的挑战和机遇。例如，对于数据购买者来说，探索如何在数据卖家之间分配预算以最大限度地提高所购买数据集的效用是很有趣的。对于数据销售商来说，根据供求关系为其数据集的不同部分分配价格非常重要，这样数据卖家及其数据集就可以在市场上保持竞争力。

  最后，需要开发严格的数据定价模型评估方法。许多现有的定价模型只是在过于简化的实验环境中评估的，其中许多假设都是对市场参与者的行为做出的。然而，理论上合理的模型在实践中可能不起作用，因为某些模型假设可能会中断。例如，在现实世界的市场中，参与者可能有对抗性、无知或建立联盟的行为。然而，这些行为对定价模型性能的影响在详细分析中在很大程度上被忽视了。因此，正如Fernandez等人[30]所建议的那样，应该开发一个可以模拟市场参与者不同行为的模拟平台。该平台可以帮助我们研究目标环境中定价模型的优势和局限性，并选择最佳部署模型。