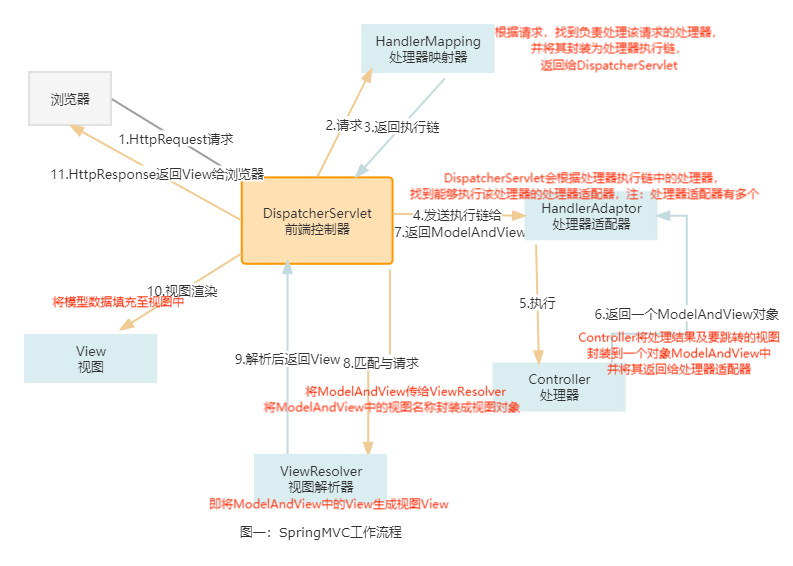
https://vjudge.net/problem/Gym-103118B/origin

在猫的国度里,有n个城市。猫国国王想要修n -1条路来连接所有的城市。第i市有一家ai经验价值的建筑公司。要在第i市和第j市之间修建公路,两个城市的建筑公司需要相互合作。但是,在修路的过程中,两家施工公司可能会因为沟通不畅而发生冲突,会造成建筑材料的浪费。从形式上讲,在第i个城市和第j个城市之间修建公路将浪费ged(ai, aj)建筑材料。你能帮助猫国国王选择建造n - 1条连接所有城市的道路,并最大限度地减少建筑材料的浪费吗?为了减少输入大小,猫国的国王给你一个随机整数生成器和3个参数L, R,种子。下面的C语言代码展示了如何生成n个整数a1, a2,…, an, a[i]存储第i个城市建筑公司的经验值。您可以在提交的文件中直接使用代码。
题解:
这道题本身并不是一道难题,
本身就一个最小生成树求出最小距离即可
但是边数n^2,正常求边肯定会t
关键是能否想到n > 某一个之后,答案只会是n - 1
正常来想的话是很难想到这一点的,由于我本身也不太明白,所以无法证明这一点
但是我么可以通过打表发现,当n > 5后,答案就都是n - 1了
(打表是一种很重要的思想,并且这题只用输入四个数即可,是和容易打表的,遇到一些难以解决的问题时,打表不失为一种好的选择)
此外通过他给我们的函数发现

如果R = L那么所有a[i]均为L那么答案就是(n-1)*L
#include<iostream> #include<algorithm> #include<string> #include<cstring> #include<vector> #include<map> #include<queue> using namespace std; #define int long long const int N = 4e6 + 10; typedef pair<int, int> PII; unsigned long long seed; int R,L; unsigned long long xorshift64() { unsigned long long x=seed; x^=x<<13; x^=x>>7; x^=x<<17; return seed=x; } int f[N]; int gen(){ return xorshift64()%(R-L+1)+L; } int n; int a[N]; struct node { int l,r,x; friend operator <(const node &a,const node &b) { return a.x < b.x; } }p[N]; int find(int x) { if(f[x] == x) return x; return f[x] = find(f[x]); } void solve() { cin >> n >> L >> R >> seed; for(int i = 1;i <= n;i++) a[i] = gen(); if( L == R) { cout <<(n - 1)*L; return ; } if(n > 5) { cout << n - 1<<"\n"; return ; } int cnt = 0; for(int i = 1;i <= n;i++) { for(int j = i + 1;j <= n;j++) { p[++cnt].l = i; p[cnt].r = j; p[cnt].x = __gcd(a[i],a[j]); } } for(int i = 1;i <= n;i++) { f[i] = i; } sort(p+1,p+1+cnt); int ans = 0; int w = 0; for(int i = 1;i <= cnt;i++) { int x = find(p[i].l); int y = find(p[i].r); if(x != y) { f[y] = x; ans += p[i].x; w ++; } if(w == n-1) break; } cout << ans; } signed main() { // ios::sync_with_stdio(0); // cin.tie(0);cout.tie(0); int t = 1; // cin >> t; //scanf("%lld",&t); while (t--) { solve(); } } //3 F //5 B //6 F //9 F //10 B //12 F //15 FB //18 FB