1 曲线曲线

1.1 直线/二次曲线

直接解析法计算交点。

1.2 二次曲线/二次曲线

// Todo

1.3 其他类型

// Todo

2 曲线曲面

2.1 直线/二次曲面，二次曲线/平面

直接解析法计算交点。

2.2 二次曲线/二次曲面

// Todo

2.3 其他类型

// Todo

3 曲面曲面

3.1 平面/二次曲面

直接解析法计算交线。

3.2 二次曲面/二次曲面

// Todo

3.3 其他类型

（1995年4月）隐式曲面／参数曲面的求交算法 （冉瑞江 王亚平 唐荣锡/北航飞行器制造工程系）

思路：

• 1.将n次代数曲面方程用齐次坐标的表示；
• 2.将参数曲面用NURBS表示，然后插入重复节点，变成一组有理Bezier曲面，平且改写成齐次幂级数形式；
• 3.将2中的齐次坐标表示代入1中，得到关于参数u、v的方程。（该方程就表示uv参数域的一条平面曲线）；

然后分析讨论平面代数曲线$F(u,v)=0$的性质。

追踪：
在跟踪之前，对于每一个特征初始点，记录其连接次数，即从该点开始或者终止的单调分枝数。

估算下一个点：用切线、或者用密切圆的方法计算近似点
计算精确的下一个点：

注意：一点想法和改进，这个地方需要两次迭代计算两个最近点，会不会是效率降低？
我使用的方法是，直接把当前点作为初始值，放入方程组中迭代，会得到一个精确交点。这样计算次数会不会少一些？但是存在一种可能，就是可能得到的新的点离当前初值点跑了一些距离。不知道本文中用两个最近点的迭代会不会存在这种问题？

文中说到：跟踪时要 注 意 不 要 进 入 交 线 的另一 分枝 和 重 复 跟 踪 同 一 交线分枝， 算 法可 靠性的关键在于适当控制步长和精度 。

// 这和我当时做求交考虑到的不谋而合。

// 这个地方我当时做求交的时候也考虑到了，为了避免这种情况，会在出参数域的时候做一个判断，当跨出参数域的那一刻，与边界计算出精确的交点，并停止继续计算边界外的交点。

（1997年12月）平面向量场与曲率分析在曲面求交中的应用（宁涛 马德昌 王亚平 唐荣锡/北航飞行器制造工程系）

在 曲面 求 交 的 跟 踪 算法 中，主 要 有 三 项关 键 技 术：（1）初 始跟 踪 点集 完 备 性（2） 数 值 方法稳 定 性（3）误差准则一致性。

如果找 到 两 张 曲 面 的所有 共 线法 矢， 沿共线 法 矢 点对 两 曲面 进 行分割，那 么 所得 到 的小曲面 片 没 有交线 环. 这 样 就保 证 了不 遗漏 任何交线 环.

对于相切点的位置追踪方向的计算：

//这个计算方法和我当时做求交的时候，处理相切情况计算切向的方法一样。并且确实可能会出现多解情况，也就是交线会在这个地方出现多个分支。最好根据前一次的跟踪方向，来确定当前走哪个分支，这样计算的交线走向更自然。
跟踪步长的计算方法：

//“ 根据 曲 率估 计 跟 踪步长 是 毫无 意 义 的”。确实如此，在实际工程中，我在估算跟踪步长的时候，虽然通过曲率计算得到估计步长，但还要做其他的限制处理。并且步长的估算公式最好是连续变化的。
对于相切点的位置跟踪步长的计算方法：

// 看起来这个估算曲率的方法也不错。因为曲率本来是用来估算步长的，不需要精确，所以采用本文中的方法似乎是个不错的选择。
// 我做求交采用的是利用更高阶偏微分计算相切点的曲率，计算方法可以从某一篇分析交线的微分的论文中找到。但是采用更高阶偏微分计算曲率计算量比较大，并且不是很稳定，因为可能像nurbs曲面没有连续的更高阶的微分。

曲 面 求 交 的 主 程 序 由三 部分构成：（1）计算 两 张 曲 面 的 包 围 盒，利用包 围盒 进 行求交粗判；（2） 计算 两张 曲 面 形 成的平 面 向 量 场， 用Kriezis方 法 求 出 临界 点。然 后， 利用 曲线/曲 面 求交算 法 计算 初始跟踪点 和 跟踪 方 向。（3）对外部 初 始跟 踪点 和 内 部 初 始 跟 踪 点分别 进行 跟 踪，得到 所有 交 线。外 部初始跟踪点 是 指 至 少在一 张 曲 面 边 界上 的 初 始跟 踪点，内部 初 始 跟 踪点 是指 不 在 任何 一张 曲 面 边界 上 的 初 始跟踪 点.

当跟踪完 所有 外 部 初 始 跟踪 点 后， 所得交线均与曲 面 边 界 有交。如 果此 时 内 部 初 始跟 踪点集非 空， 那 么两 曲 面 有 内部交 线 环。对 内 部 交 线 环的 跟 踪 较 为 简 单， 这 里 不再介 绍。
对外部初始跟踪 点 的 跟 踪 过 程：

// 这里对于外部跟踪点的处理和我当时做求交实现的方法基本一样。
// 或者说其实本文中所描述的求交的理论方法，和我当时在实践中摸索的的实现曲面求交的方法基本完全一致。所以本文很具有实用价值，提到了很多工程实现时的关键问题。

（1999年3月）一种参数曲面与隐式曲面的求交算法（余正 彭群生 马利庄/浙江大学CAD＆CG）

生成$h(u,v)＝0$的等值线，其主要算法步骤如下：
1） 逐个计算每一网格单元与等值线的交点；
2） 连接该单元与等值线的交点，生成该单元内的一等值线的线段；
3） 由一系列单元内的等值线的线段构成该网格中的等值线．
计算单元的各边与等值线的交点，假设函数 h（ u，v） 在单元内呈线性变化，可以采用顶点判定和边上插值的方法计算交点，具体步骤如下：

图(a)二维标量场抽取参数曲面的参数域的等值线，该等值线在参数曲面上的映射，便得到参数曲面与隐式曲面的交线c，如下图（b）。

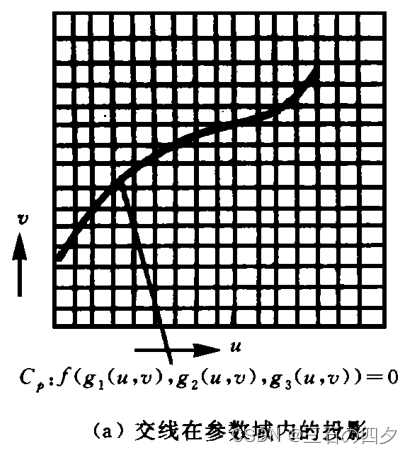
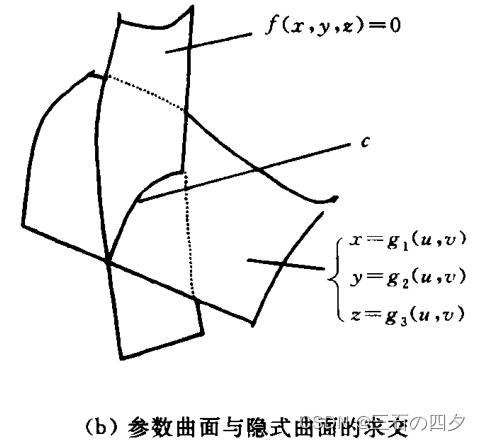
评论：对于计算初始点，用网格法，计算h（ u，v）不用迭代也很快，确实不失为一个好方法。但是网格划分的密度是一个问题，划分太密计算量也很巨大，划分太稀可能会漏掉某些初始点（譬如说小环或者孤立点）。

（2004年）圆环与圆环求交算法中初始点的计算 （王日昀 宁涛 席平 唐荣锡/北航飞行器制造工程系）

在曲面求交方面做了大量的研究并相继推出很多优秀的算法 [1]~[5] 。算法大体上可归为 4 类：
分割法 （subdivision method），网格计算法 (lattice evaluation)，几何法 (geometric method)，追踪法 (marching method)。

先通过某种求交方法确定各交线环上的一个交点，根据交线的几何性质，按照一定步长计算该条交线上下一交点的近似值，再应用迭代法求得精确的交点。沿交线走向不断前进，直至遍历整条交线。追踪法求交的原理如图 1 所示。

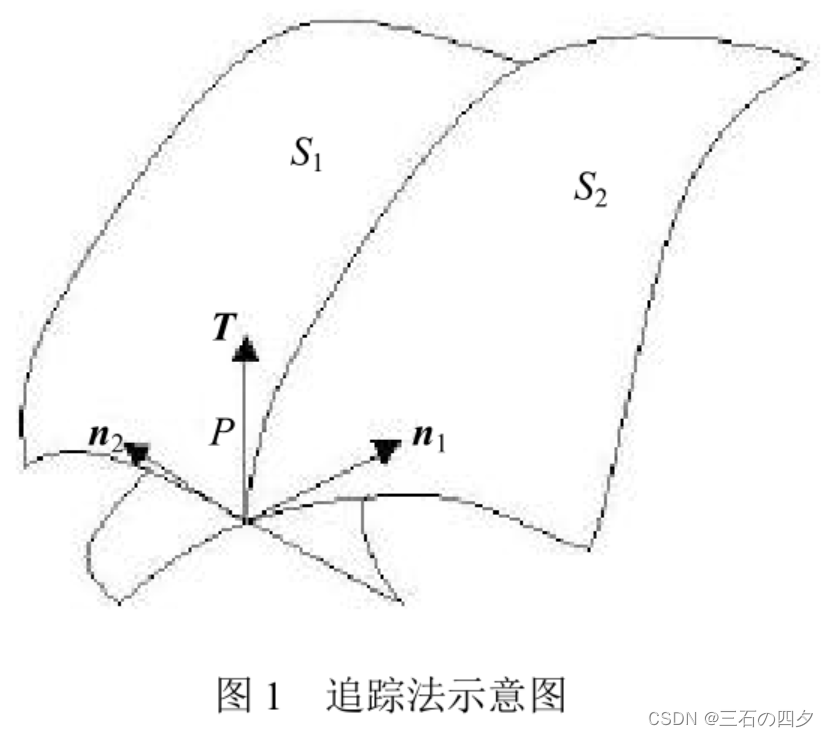
追踪法求交的优点是在求得首交点后搜索交线的其余交点的速度非常快，且适用范围广。参数曲面，只要曲面不存在非正则点，并可以求得曲面上任意点的坐标位置、法矢、切矢等几何信息，就可以用追踪法求交。
缺点：追踪法的问题是目前尚无有效的方法来求得所有交线的初始点。在有些情况下寻求初始点所花费的时间远大于追踪过程所节省的时间，而为了节省寻求初始点的时间，又可能漏掉某些交线，当在孤立交点和比较小的交线环时尤甚。

交线类型分析：
一般曲面相交交线类型包括：开环线，闭环线，尖点，切点。而在圆环与圆环相交中不存在开环线，且尖点也是以切点的形式存在，所以主要任务就是发现所有的切点，并计算出闭环线的初始点。

评论：这个分析方法不是很好，而且会用到了在接近的区域细分，实现起来复杂，性能可能也一般。
我的思路：对于两个圆环面，是否可以考虑第二个圆环面中心圆和内外圆在第一个圆的平面上的投影曲线（二次曲线），然后计算二次曲线之间的交点，估算出大概的相交区域，然后利用附近位置的等参线（截面圆）与另外一个圆环计算交点（作为初始交点），或者在这种区域附近将两个圆环面细分计算初始交点。

（2005年6月）圆环面/球面求交算法 （陈小雕 雍俊海 郑国勤 孙家广/清华计算机科学与技术系）

求交算法在保持拓扑稳定性上仍然存在着两大问题：一是求交分支漏解，二是使用跟踪法时在某些情况下会发生分支跳跃。

本文结合点圆最近距离计算与区间中点测试求交方法［11］提出了统一求解所有三种类型的圆环面/球面求交问题的算法。
（注：球面（球心）与圆环面的最近距离是不是也不难计算？是不是可以利用一下，对求交有帮助？）。正好，论文中也利用了一些方法，计算了球心到圆环面的最小和最大平方距离。

$\Delta ＝l_1^2＋l_2^2＋l_3^2$（6）
其中:
$$\begin{gathered} l_1＝－2r（x_{0}cosu＋y_{0}sinu－R） \\ {l}_2＝－2r{z}_0 \\ {l}_3＝x_0^2＋y_0^2＋z_0^2＋r^2＋R^2－{\delta }^2－2R（x_{0}cosu＋y_{0}sinu） \end{gathered}$$

若$l_1$,$l_2$ 全为0，则圆 U 在球面上或者与球面无交；否则Δ的符号与圆U 和球面的相异交点的个数有如下关系:
Δ＞0有两个相异交点
Δ＝0有一个相异交点
Δ＜0没有交点

式（6） 对交曲线的拓扑结构分析来说很重要，故称它为关键方程。

圆环面和球面最多只有两条交线？？？？

评论：很有效的方法，可以实际中实现用起来。

（2007年）采用“结式法”的圆环面和球面求交算法（谌炎辉 徐武彬/广西工学院机械系）

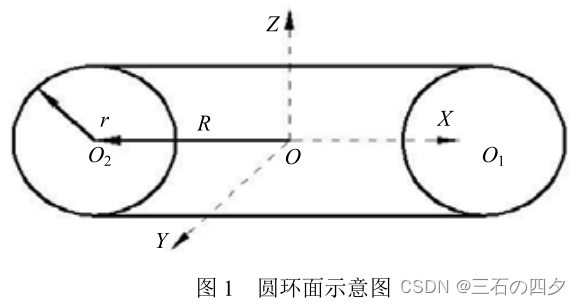
讨论圆环面小圆和球面截圆(指球面在XOZ平面上所截的圆)的位置关系给出了圆环面和球面不相交、交线为圆、交线为孤立点、交线中自交点和尖点及交线的区间等。

评论：这篇文章与上一篇文章基本相似，只不过讲述的偏几何一点（上一篇更偏代数），更容易理解一点。

思路：可用如下两个方向的投影快速判断有没有交和交的大概位置。

（1976）Levin J∙A parametric algorithmfor drawing pictures of solid ob-jects composed of quadric surfaces ［J］∙Communications of the ACM‚1976‚19（10）

（1995）Miller J ‚Goldman R∙Geometric algorithms for detecting and calculating all conic sections in theintersection of any t wo natural quadric surfaces ［J］∙Graphical Models and I mage Processing ‚1995‚57（1） ：55～66

（1989）Peigl L∙Constructive method of intersecting natural quadrics representedin tri mmed surface for m ［J］∙Computer-Aided De-sign ‚1989‚21（4） ：201～212

（1983）Sarraga R∙Algebraic methods for intersections of quadric sur-faces in GMSOLI D［J］∙Computer Vision ‚Graphics and I mage Processing ‚1983‚22（2） ：222～238

（1998）Ki m K‚Ki m M S∙Torus/sphereintersection based on a configu-ration space approach ［J］∙Graphical Models and I mage Process-ing ‚1998‚60（1） ：77～92

（1998）Zuo Zheng∙Intersection ‚classification and application of geo-metric modeling ［ D］∙Beijing ：Tsinghua University ‚1998（in Chinese）（ 左　 征∙几何造型中的求交分类及其应用［ 博士学位论文］∙北京：清华大学‚1998）

等

//Todo
// 未完，更新中

注

注：1.若有写的不当之处还请谅解并指正。2.以上论文标题即为出处引用，后面就不再单独做详细的文献引用。