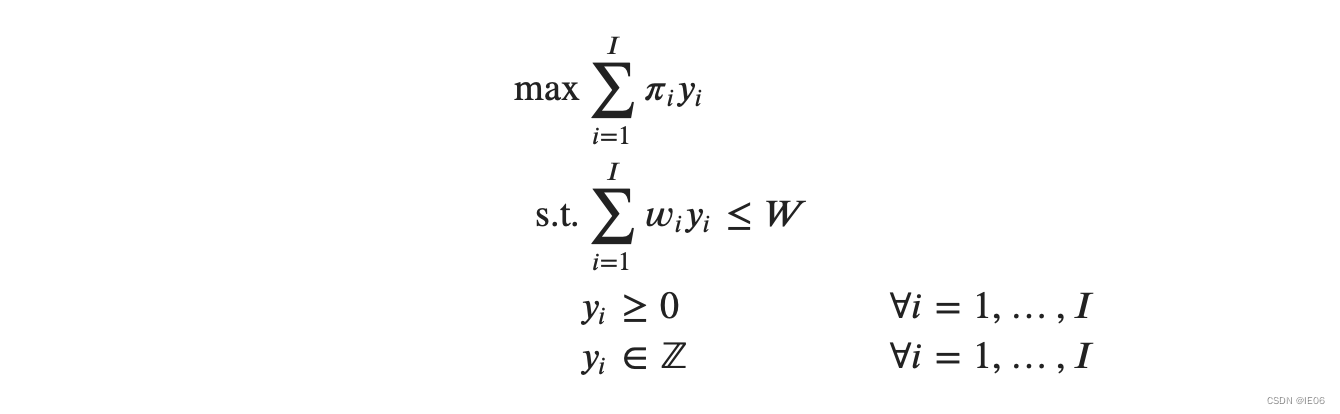文章目录

一、简单数学问题习题练习

1、1 买不到的数目

1、1、1 题目描述

1、1、2 题解关键思路与解答

1、2 饮料换购

1、2、1 题目描述

1、2、2 题解关键思路与解答

二、DP问题习题练习

2、1 背包问题

2、1、1 题目描述

2、1、2 题解关键思路与解答

2、2 摘花生

2、2、1 题目描述

2、2、2 题解关键思路与解答

2、3 最长上升子序列

2、3、1 题目描述

2、3、2 题解关键思路和解答

三、总结

标题：蓝桥杯——数学与简单DP问题习题练习

作者：@Ggggggtm

寄语：与其忙着诉苦，不如低头赶路，奋路前行，终将遇到一番好风景

一、简单数学问题习题练习

蓝桥杯比赛中常见的还有一类数学问题，这些数学问题有的是有公式计算，有的是考察的思维逻辑。我们具体来看例题。

1、1 买不到的数目

1、1、1 题目描述

题目来源：第四届蓝桥杯省赛C++A组,第四届蓝桥杯省赛JAVAC组

题目难度：简单

题目描述：小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式：

两个正整数 n,m，表示每种包装中糖的颗数。

输出格式：

一个正整数，表示最大不能买到的糖数。

数据范围：

2≤n,m≤1000，
保证数据一定有解。

输入样例：
4 7
输出样例：
17

1、1、2 题解关键思路与解答

我们先关插题目，是两个数找到这两个数最大凑不出来的数。当两个数是由除1外还有其他的公约数时，我们发现并不能找到这两个数最大凑不出来的数。也就是当两个数互质时，才能够找出这两个数最大凑不出来的数。这里是有一个公式的，我们假设这两个数分别是p、q，两个数互质，那么求这两个数最大凑不出来的数的公式为：（p-1）*（q-1）-1。我们看一下本题的代码。

#include<iostream>

using namespace std;

int p,q;

int main()
{
    cin>>p>>q;
    
    cout<<(p-1)*(q-1)-1;
    return 0;
}

1、2 饮料换购

1、2、1 题目描述

题目来源：第六届蓝桥杯省赛C++A/C组,第六届蓝桥杯省赛JAVAB组

题目难度：简单

题目描述：乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料，凭3个瓶盖可以再换一瓶C型饮料，并且可以一直循环下去(但不允许暂借或赊账)。请你计算一下，如果小明不浪费瓶盖，尽量地参加活动，那么，对于他初始买入的 n 瓶饮料，最后他一共能喝到多少瓶饮料。

输入格式：

输入一个整数 n,表示初始买入的饮料数量。

输出格式：

输出一个整数，表示一共能够喝到的饮料数量。

数据范围：

0<n<10000。

输入样例：
100
输出样例：
149

1、2、2 题解关键思路与解答

本题目主要考察的是思维逻辑能力。我们要注意的是本题有一个陷阱，就是我们需要注意用瓶盖换瓶子的时候可能会有剩余，下次再换的时候我们的瓶盖数量就是已经换购的饮料数量加喝完上上次剩下的瓶盖数量。我们直接看代码。

#include<iostream>

using namespace std;

int n;

int main()
{
    cin>>n;
    
    int sum=n;
    
    int ret=n;
    while(ret >= 3)
    {
        sum+=ret/3;
        ret=ret/3+ret%3;
    }
    cout<< sum;
    return 0;
}

二、DP问题习题练习

2、1 背包问题

2、1、1 题目描述

题目来源：AcWing

题目难度：简单

题目描述：有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式：

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式：

输出一个整数，表示最大价值。

数据范围：

0<N,V≤1000，
0<vi,wi≤1000。

输入样例：
4 5
1 2
2 4
3 4
4 5
输出样例：
8

2、1、2 题解关键思路与解答

这里我们用闫氏DP分析法进行分析：上述思想的关键就是状态计算。我们不选第 i 个物品时，其前 i-1个物品的总价值和为 f[i-1][j]，那么第 i 个物品的价值也为 f[i-1][j]。如我们选上第 i 个物品时，计算其价值为前 i-1 个物品的价值表示为 f[i-1][j-v[i]]，那么选上第i个物品的价值为 f[i-1][j-v[i]] + w[i]。在两者值减去一个较大的就行。我们看代码的实现。

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N =1010;

int f[N][N];

int n,m;

int v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];
        
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            
            if(j>=v[i])
                f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    
    cout<<f[n][m]<<endl;
    return 0;
}

2、2 摘花生

2、2、1 题目描述

题目来源：《信息学奥赛一本通》

题目难度：简单

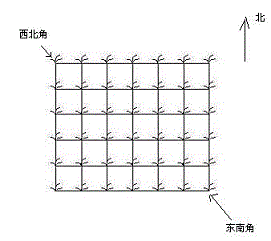
题目描述：Hello Kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty只能向东或向南走，不能向西或向北走。问Hello Kitty最多能够摘到多少颗花生。

输入格式：

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式：

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围：

1≤T≤100,
1≤R,C≤100,
0≤M≤1000。

输入样例：
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例：
8
16

2、2、2 题解关键思路与解答

该题我们同样用闫氏DP分析法：状态计算中的集合划分大部分情况下的依据是最后不相同的一步。这道题就是走到右下角只能是从正上走过来，或者正左走过来。我们只需要选出这两者的较大的一个，再加上右下角的花生数量即可。我们结合着代码一起理解一下。

#include<iostream>

using namespace std;

const int N=110;

int f[N][N],w[N][N];

int n,m;

int main()
{
    int T=0;
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                scanf("%d",&w[i][j]);
            }
        }
        
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j];
            }
        }
        cout<<f[n][m]<<endl;
    }
    return 0;
}

2、3 最长上升子序列

2、3、1 题目描述

题目来源：AcWing

题目难度：简单

题目描述：给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式：

第一行包含整数 N。

第二行包含 N 个整数，表示完整序列。

输出格式：

输出一个整数，表示最大长度。

数据范围：

1≤N≤1000，
−1e9≤数列中的数≤1e9。

输入样例：
7
3 1 2 1 8 5 6
输出样例：
4

2、3、2 题解关键思路和解答

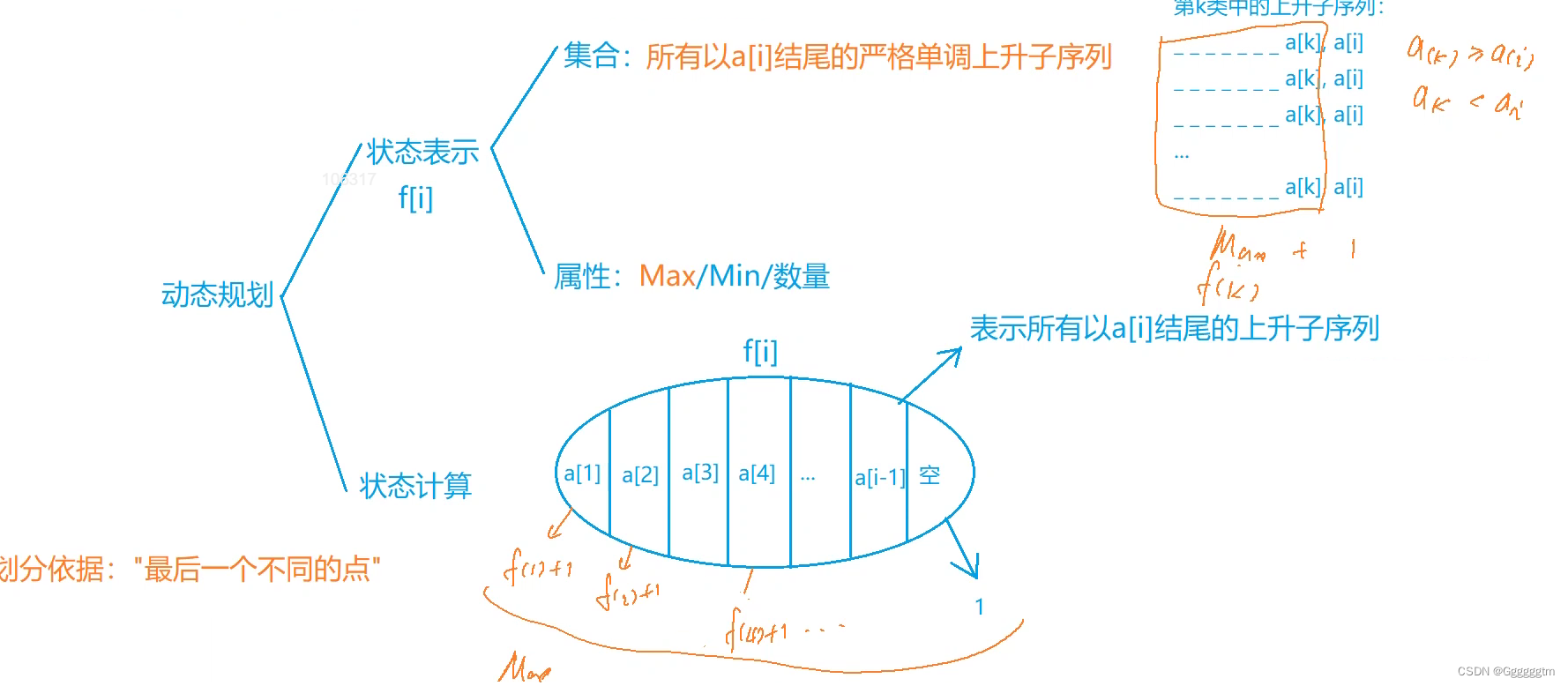
该题目可能会给很多同学造成一个错误的理解。题目中的要求是求数值严格单调递增的子序列的长度最长是多少，指的是不是连续的也行。如上述案例，最大上升子序列为：1，2，5，6。那该怎么求呢？我们用闫氏DP法进行分析：

这里关键的就是我们枚举出以i结尾的最大的长度即可。最后在从不同结尾当中找出最大值。那我们怎么计算出以i结尾的最大长度呢？我们只需要在i之前，且比 a[i] 的就行，更新 f[i] 的值即可。我们结合着代码一起理解一下：

#include<iostream>

using namespace std;

const int N=1010;

int a[N],f[N];

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    
    for(int i=1;i<=n;i++)
    {
        f[i]=1;
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
                f[i]=max(f[i],f[j]+1);
        }
    }
    
    int res=0;
    for(int i=1;i<=n;i++)
        res=max(res,f[i]);
        
    cout<<res;
    return 0;
}