1. 案例建模

我们对cutting stock问题进行建模。rolls的尺寸为W，每个型号的需求量和尺寸分别为d和w，如下：

struct Piece
    w::Float64
    d::Int
end

struct Data
    pieces::Vector{Piece}
    W::Float64
end

function Base.show(io::IO, d::Data)
    println(io, "Data for the cutting stock problem:")
    println(io, "  W = $(d.W)")
    println(io, "with pieces:")
    println(io, "   i   w_i d_i")
    println(io, "  ------------")
    for (i, p) in enumerate(d.pieces)
        println(io, lpad(i, 4), " ", lpad(p.w, 5), " ", lpad(p.d, 3))
    end
    return
end

function get_data()
    data = [
        75.0 38
        75.0 44
        75.0 30
        75.0 41
        75.0 36
        53.8 33
        53.0 36
        51.0 41
        50.2 35
        32.2 37
        30.8 44
        29.8 49
        20.1 37
        16.2 36
        14.5 42
        11.0 33
        8.6 47
        8.2 35
        6.6 49
        5.1 42
    ]
    return Data([Piece(data[i, 1], data[i, 2]) for i in axes(data, 1)], 100.0)
end

data = get_data()

模型为：

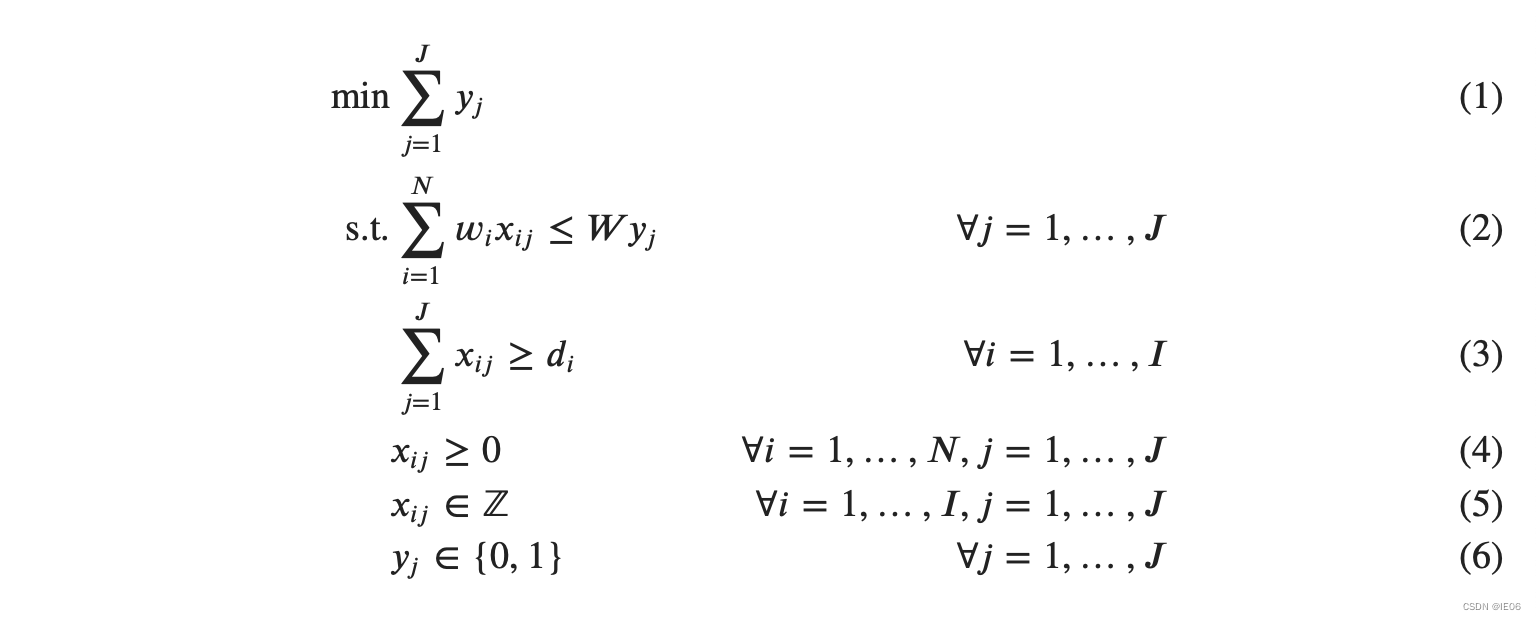
建模入下：

I = length(data.pieces)
J = 1000  # Some large number
model = Model(GLPK.Optimizer)
@variable(model, x[1:I, 1:J] >= 0, Int)
@variable(model, y[1:J], Bin)
@constraint(
    model,
    [j in 1:J],
    sum(data.pieces[i].w * x[i, j] for i in 1:I) <= data.W * y[j],
)
@constraint(model, [i in 1:I], sum(x[i, j] for j in 1:J) >= data.pieces[i].d)
@objective(model, Min, sum(y[j] for j in 1:J))
model

2. 转为列生成

2.1 另一种建模方式

枚举每一roll可能的切割方式𝑝=1,…,𝑃，称为 cutting patterns。 $a_{i,p}$指的是有多少个piece i在cutting pattern p中，则模型为：

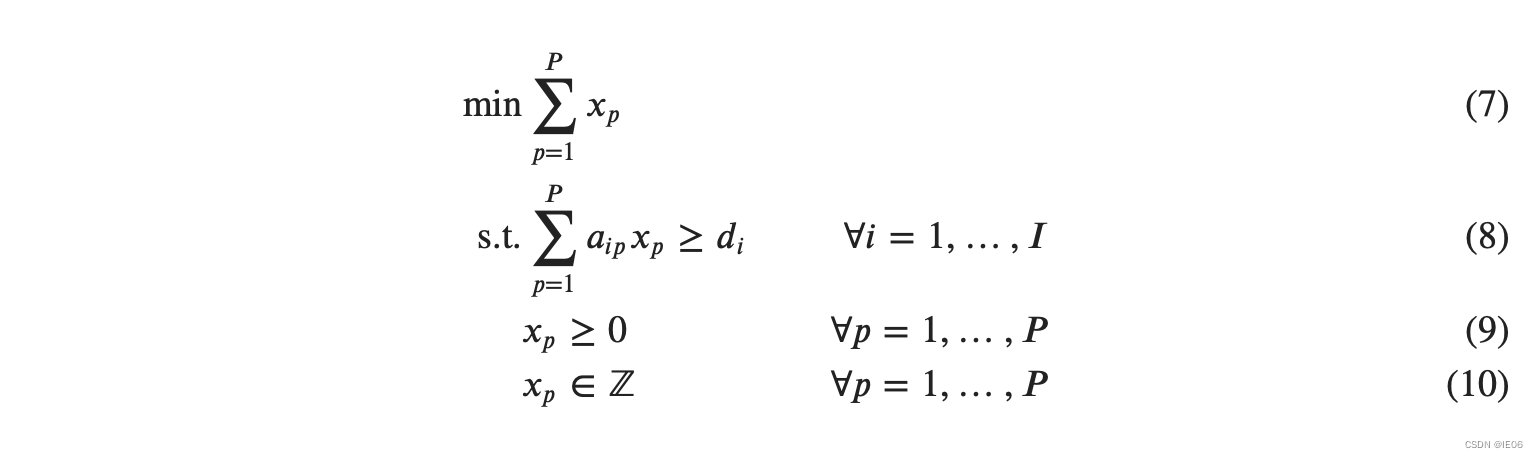
最开始我们只列出少数几种pattern，然后通过一定的方式生成更多的pattern不断求解。初始的pattern可以简单设置，比如每个pattern中只有一个型号：

patterns = Vector{Int}[]
for i in 1:I
    pattern = zeros(Int, I)
    pattern[i] = floor(Int, min(data.W / data.pieces[i].w, data.pieces[i].d))
    push!(patterns, pattern)
end
P = length(patterns)

model = Model(GLPK.Optimizer)
set_silent(model)
@variable(model, x[1:P] >= 0)
@objective(model, Min, sum(x))
@constraint(model, demand[i = 1:I], patterns[i]' * x == data.pieces[i].d)
model

2.2 生成新column的子问题

子问题称为pricing problem，令$y_i$为新的column中第i个型号的数量，则必须满足总尺寸<=W
主问题的对偶解可以理解为：第i个piece每一个单位的需求对应的rolls数目。
那么子问题中的column满足原先$y_i$个需求，总共会节省的rolls数目，将其最大化：

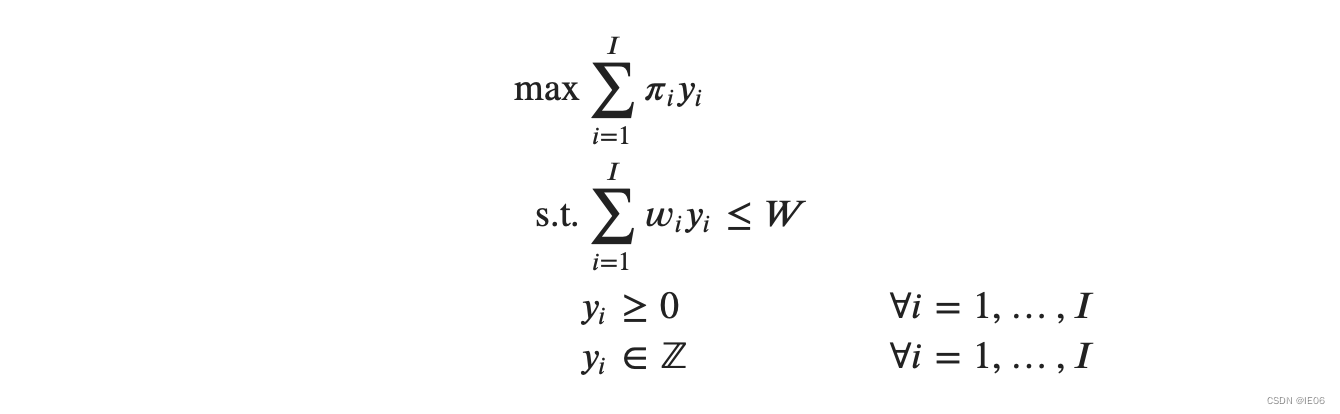
如果这个目标函数>1，那么这就是个省钱的交易。

function solve_pricing(data::Data, π::Vector{Float64})
    I = length(π)
    model = Model(GLPK.Optimizer)
    set_silent(model)
    @variable(model, y[1:I] >= 0, Int)
    @constraint(model, sum(data.pieces[i].w * y[i] for i in 1:I) <= data.W)
    @objective(model, Max, sum(π[i] * y[i] for i in 1:I))
    optimize!(model)
    if objective_value(model) > 1
        return round.(Int, value.(y))
    end
    return nothing
end

2.3 求解过程

while true
    # Solve the linear relaxation
    optimize!(model)
    # Obtain a new dual vector
    π = dual.(demand)
    # Solve the pricing problem
    new_pattern = solve_pricing(data, π)
    # Stop iterating if there is no new pattern
    if new_pattern === nothing
        break
    end
    push!(patterns, new_pattern)
    # Create a new column
    push!(x, @variable(model, lower_bound = 0))
    # Update the objective coefficients
    set_objective_coefficient(model, x[end], 1.0)
    # Update the non-zeros in the coefficient matrix
    for i in 1:I
        if new_pattern[i] > 0
            set_normalized_coefficient(demand[i], x[end], new_pattern[i])
        end
    end
end

patterns数组用来存储每次新添加的组合方式。将结果打印出来：

set_integer.(x)
optimize!(model)
for p in 1:length(x)
    v = round(Int, value(x[p]))
    if v > 0
        println(lpad(v, 2), " roll(s) of pattern $p, each roll of which makes:")
        for i in 1:I
            if patterns[p][i] > 0
                println("  ", patterns[p][i], " unit(s) of piece $i")
            end
        end
    end
end
total_rolls = sum(ceil.(Int, value.(x)))