1.概述

支持向量机（SVM，支持向量网络），是机器学习中获得关注最多的算法没有之一。它源于统计学习理论。
|
|
|

	功能
有监督学习	线性二分类与多分类（Linear Support Vector Classification）非线性二分类与多分类（Support Vector Classification, SVC）普通连续型变量的回归（Support Vector Regression）概率型连续变量的回归（Bayesian SVM）
–	–
无监督学习	支持向量聚类（Support Vector Clustering，SVC）异常值检测（One-class SVM）
–	–
半监督学习	转导支持向量机（Transductive Support Vector Machines，TSVM）

1.1支持向量机分类器是如何工作的

支持向量机所作的事情其实非常容易理解。先来看看下面这一组数据的分布，这是一组两种标签的数据，两种标签分别由圆和方块代表。支持向量机的分类方法，是在这组分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量接近于小，尤其是在未知数据集上的分类误差（泛化误差）尽量小。
超平面
在几何中，超平面是一个空间的子空间，它是维度比所在空间小一维的空间。 如果数据空间本身是三维的，则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。在二分类问题中，如果一个超平面能够将数据划分为两个集合，其中每个集合中包含单独的一个类别，我们就说这个超平面是数据的“决策边界‘“。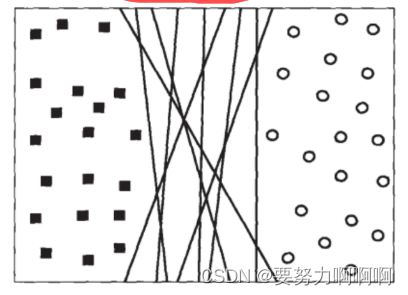
这个例子表现出，拥有更大边际的决策边界在分类中的泛化误差更小，这一点可以由结构风险最小化定律来证明（SRM）。如果边际很小，则任何轻微扰动都会对决策边界的分类产生很大的影响。边际很小的情况，是一种模型在训练集上表现很好，却在测试集上表现糟糕的情况，所以会“过拟合”。所以我们在找寻决策边界的时候，希望边际越大越好。

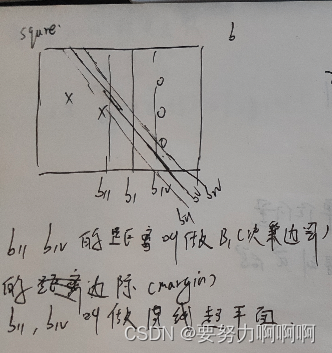
支持向量机，就是通过找出边际最大的决策边界，来对数据进行分类的分类器。也因此，支持向量分类器又叫做最大边际分类器。

1.2线性SVM的拉格朗日对偶函数和决策函数

**将损失函数从最初形态转换为拉格朗日乘数形态。**我们的损失函数是二次的(quadratic)，并且我们损失函数中的约束条件在参数w和b下是线性的，求解这样的损失函数被称为“凸优化问题”(convex optimization problem)。拉格朗日乘数法正好可以用来解决凸优化问题，这种方法也是业界常用的，用来解决带约束条件，尤其是带有不等式的约束条件的函数的数学方法。首先第一步，我们需要使用拉格朗日乘数来将损失函数改写为考虑了约束条件的形式：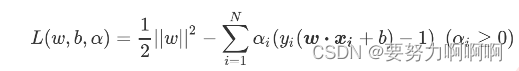
这是一个非常聪明而且巧妙的表达式，它被称为拉格朗日函数，其中 alpha就叫做拉格朗日乘数。此时此刻，我们要求解的就不只有参数向量w 和截距b 了，我们也要求解拉格朗日乘数 ，而我们的 x和 y都是我们已知的特征矩阵和标签。
将拉格朗日函数转换为拉格朗日对偶函数。