😽 PREFACE
🎁欢迎各位→点赞 👍 + 收藏 ⭐ + 评论 📝
📢系列专栏: 算法经典题集
🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用
💪 种一棵树最好是十年前其次是现在
二分
整数二分
机器人跳跃问题
机器人正在玩一个古老的基于 DOS 的游戏。
游戏中有 N+1 座建筑——从 0 到 N 编号,从左到右排列。
编号为 0 的建筑高度为 0 个单位,编号为 ii 的建筑高度为 H(i) 个单位。
起初,机器人在编号为 0 的建筑处。
每一步,它跳到下一个(右边)建筑。
假设机器人在第 kk 个建筑,且它现在的能量值是 EE,下一步它将跳到第 k+1k+1 个建筑。
如果 H(k+1)>E,那么机器人就失去 H(k+1)−E 的能量值,否则它将得到 E−H(k+1)的能量值。
游戏目标是到达第 N 个建筑,在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏,才可以保证成功完成游戏?
输入格式
第一行输入整数 N。
第二行是 N 个空格分隔的整数,H(1),H(2),…,H(N)代表建筑物的高度。
输出格式
输出一个整数,表示所需的最少单位的初始能量值上取整后的结果。
数据范围
1≤N,H(i)≤10^5,
输入样例1:
5
3 4 3 2 4
输出样例1:
4
输入样例2:
3
4 4 4
输出样例2:
4
输入样例3:
3
1 6 4
输出样例3:
3
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, h[N];
bool check(int e)
{
for (int i = 1; i <= n; i++)
{
e = e * 2 - h[i];
if (e >= 1e5) return true;
if (e < 0) return false;
}
return true;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++) cin >> h[i];
int l = 0, r = 1e5;
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << r << endl;
return 0;
}【注意点】
为什么该题可以用二分做呢? 因为题设条件满足单调性,并不是说二分就只能解决单调性,非单调性二分也能做
关于代码的11行是怎么来的,能否去掉?11行的由来是源于数学归纳法的证明,它有两个作用,一是加快代码运行速度,二是避免出现越界。如果把第十一行去掉的话,就要把e的类型改成double。
分巧克力
儿童节那天有 K 位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足:
形状是正方形,边长是整数
大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2的巧克力或者 2 块 3×3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含两个整数 Hi 和 Wi。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
数据范围
1≤N,K≤10^5
1≤Hi,Wi≤10^5
输入样例:
2 10
6 5
5 6
输出样例:
2
分析:通过观察我们发现,巧克力最后分成的总块数k和边长x具有一定关系,当x越大,我们最终分得的小巧克力块数k就越小。边长的大小与最终分得的小巧克力块数k成反比关系。既然我们最终要求的答案x恰好和k有关,并且答案所在的区间又刚好可以由k一分为二成两种不同的性质,因此本道题可以使用二分,k就是我们要找的二分边界,左边的性质我们可以描述为cheak(x)≥k,也就是说左边区间内的边长所分得的小巧克力总块数要大于等于题目要求的块数,因此我们可以由此更新左端点,使得答案区间向右边缩小,这样不仅可以求得更大的边长x,也可以找到恰好满足题意的k。
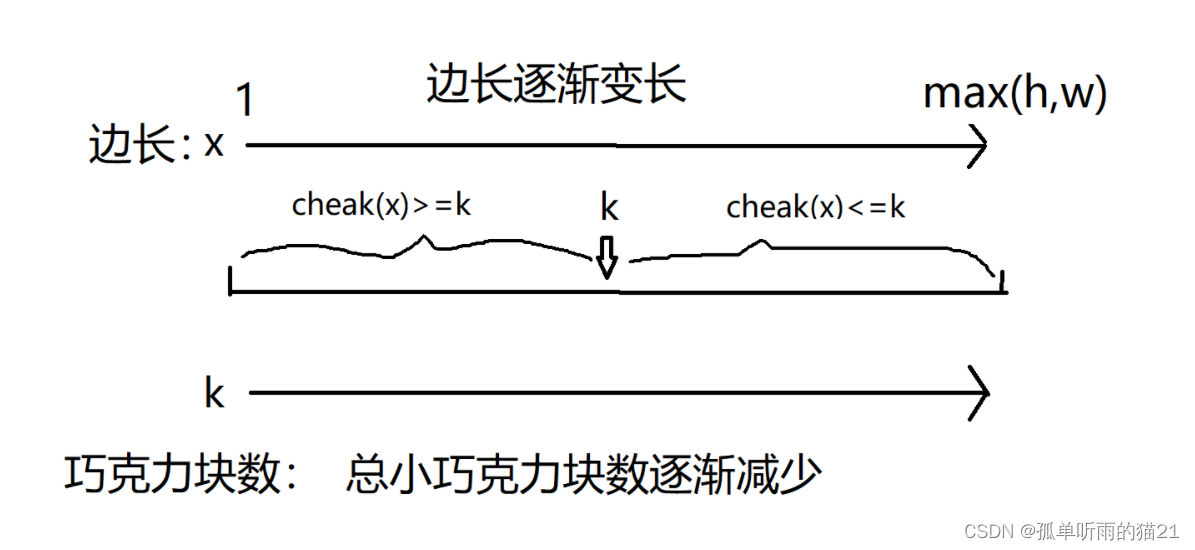
这样,我们的问题就得到了进一步简化,变成了如何设计cheak()函数,使得cheak(mid)可以刚好满足边界k的左边区间性质,这样我们便可以顺理成章的更新左端点,使得整个二分向右查找,最总找到我们所需要的答案x。
#include <iostream>
using namespace std;
int const N = 100010;
int w[N], h[N];//存储长、宽
int n, k;
bool check(int a)
{
int num = 0;//记录分成长度为 a 的巧克力数量
for (int i = 0; i < n; i++)
{
num += (w[i] / a) * (h[i] / a);//每一大块可以分成的边长为 a 的巧克力数量
if (num >= k) return true;//大于要求数量,返回真
}
return false;
}
int main()
{
cin >> n >> k;
for (int i = 0; i < n; i++) cin >> h[i] >> w[i];
int l = 1, r = 1e5;//小巧克力数量边长一定在 1 -- 100000 之间
while (l < r)//二分小巧克力边长范围,找到符合要求的最大值
{
int mid = l + (r - l + 1 >> 1);//因为l = mid ,所以 mid 取 l + r + 1 >> 1,为了防止加和越界,改写成 l + (r - l + 1 >> 1)
if (check(mid)) l = mid;
else r = mid - 1;
}
cout << r << endl;
return 0;
}跳石头

这是一道典型的二分套路题:“最小值最大化”,类似题还有“最大值最小化”。什么是“最小值最大化”呢?在所有可能的最小值中查找最大的那个值
#include <bits/stdc++.h>
using namespace std;
const int N =5e4+10;
int len,n,m;
int stone[N];
bool check(int d)//检查距离d是否合适
{
int num,pos=0;//num记录搬走岩石的数量
for(int i=1;i<=n;i++)//当前站立的岩石
{
if(stone[i]-pos<d) num++;//第i块岩石可以搬走
else pos=stone[i];//第i块岩石不能搬走
}
if(num<=m) return true;//要移动的岩石比m少,满足条件
else return false;//要移动的岩石比m多,不满足条件
}
int main()
{
cin>>len>>n>>m;
for(int i=1;i<=n;i++) cin>>stone[i];
int l=0,r=len;
while(l<r)
{
int mid=l+r+1>>1;
if(check(mid)) l=mid;//满足条件,说明mid小了,调大一点
else r=mid-1;//不满足条件,说明mid大了,调小一点
}
cout<<r<<endl;
return 0;
}实数二分
一元三次方程求解

暴力解法:
判断一个数是否为解的方法:如果函数值是连续变化的,且函数值在解的两边分别是大于0和小于0的,则解必然在它们中间。
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
double y(double x)
{
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
cin>>a>>b>>c>>d;
for(double i=-100;i<=100;i+=0.01)
{
//写法一
double j=i+0.01;
double y1=y(i),y2=y(j);
if(y1*y2<=0) printf("%.2lf ",(i+j)/2);
//写法二
if(abs(y(i))<1e-6) printf("%.2lf ",i);
}
return 0;
}二分:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
double y(double x)
{
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
cin>>a>>b>>c>>d;
for(int i=-100;i<100;i++)//题设条件给了两个根绝对值大于等于1,分200个小区间
{
double left=i,right=i+1;//题设条件给了两个根绝对值大于等于1
double y1=y(left),y2=y(right);
if(y1==0) printf("%.2lf ",left);//判断左端点
if(y1*y2<0)//小区间内有根
{
for(int j=0;j<100;j++)//在小区间内二分
{
double mid=(left+right)/2;
if(y(mid)*y(right)<=0)
left=mid;
else
right=mid;
}
printf("%.2lf ",right);
}
}
return 0;
}