pytorch入门7--自动求导和神经网络

news2024/11/25 20:34:47

深度学习网上自学学了10多天了，看了很多大神的课总是很快被劝退。终于，遇到了一位对小白友好的刘二大人，先附上链接，需要者自取：https://b23.tv/RHlDxbc。
下面是课程笔记。
一、自动求导
举例说明自动求导。
torch中的张量有两个重要属性：data（值）和grad（梯度），当我们在定义一个张量时设requires_grad=True就是说明后续可以使用自动求导机制。
在这里插入图片描述
注意：pytorch里可以设置为自动求导的张量的元素需要是浮点型。
例如，对于e=(a + b) * (b + 1)，可以用一个图表示如下：

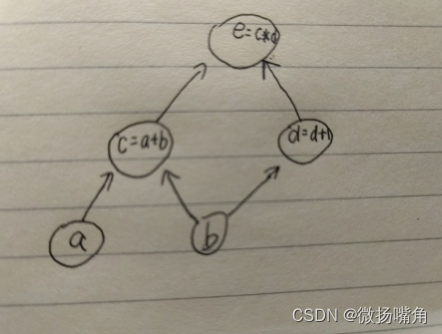
我们定义张量时通常是从下往上定义，即先定义张量a,b,再定义张量e(由张量a,b的关系式组成），这样张量e的值就由a,b得到，这就是前向传播（前馈），通常定义为forward函数：
在这里插入图片描述
当我们要进行求导时，求：

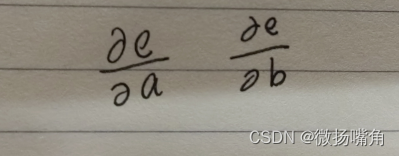
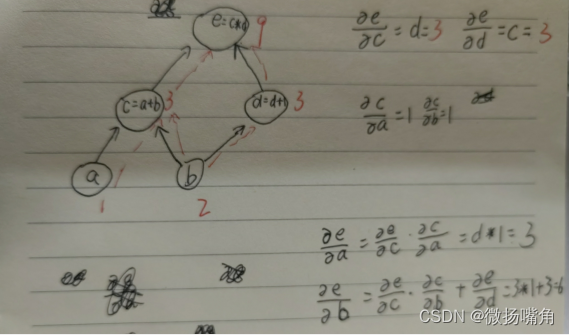
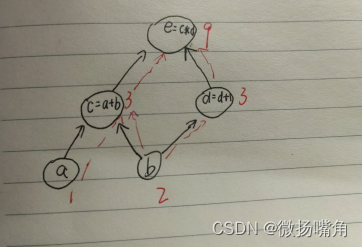
可以看出，求导是从上到下的，逐级相乘再将路径相加。比如求e对b的偏导数，,从b到e有两条路径，每条路径从e开始逐级求导，结果相乘再将多条路径求导结果相加，这个过程加反向传递（反馈），通过pytorch封装好的backward函数实现。
下面的图比我手绘的应该清楚一些：
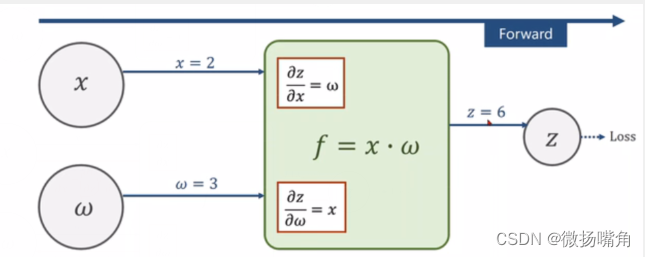
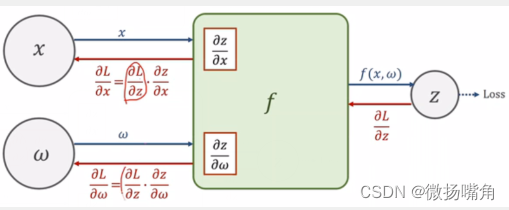
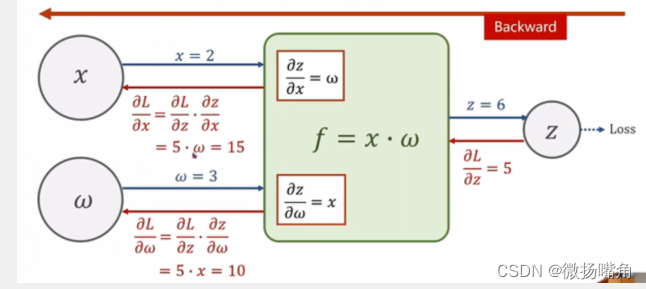
在这里插入图片描述

代码实现如下（以线性逻辑回归为例,y = w * x,给定训练数据集x,y，求最佳参数w拟合x与y的关系函数）：
我们直到在深度学习中，我们都是将损失函数对参数求导，使用梯度下降法等方法使得损失函数最好，从而找到参数的最佳值。

# 训练数据集（人眼可以一下看出y=2*x是最好的拟合，但机器不知道，要一直训练
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0] 

# 参数w，初始值设为1.0
w = torch.tensor([1.0],requires_grad=True)

# 前向传播
def forward(x):
    return x * w

# 损失函数
def loss(x,y):
    y_pred = forward(x) # y_pred即为常说的y_hat，是y在当前w的值下计算的估计值，这里即建立了y_pred与w的关系，可以自动求导
    return (y_pred - y) ** 2

# 训练数据集（梯度下降法）
for epoch in range(1000):
    for x,y in zip(x_data,y_data):
        l = loss(x,y)
        l.backward() # 自动求导，l对w求导，反向传播
        print('\tgrad:',x,y,w,w.grad.item()) # item()用于只含一个元素的tensor中提取值
        w.data = w.data - 0.01 * w.grad.data # **这里使用data属性就是为了防止使用自动求导机制**
        w.grad.data.zero_() # 将上一轮的梯度值清除
    print("progress:",epoch,l.item())

# 测试结果
print("predict(after training)",4,forward(4).item()) # 计算当x=4时，根据训练出的模型求y的估计值

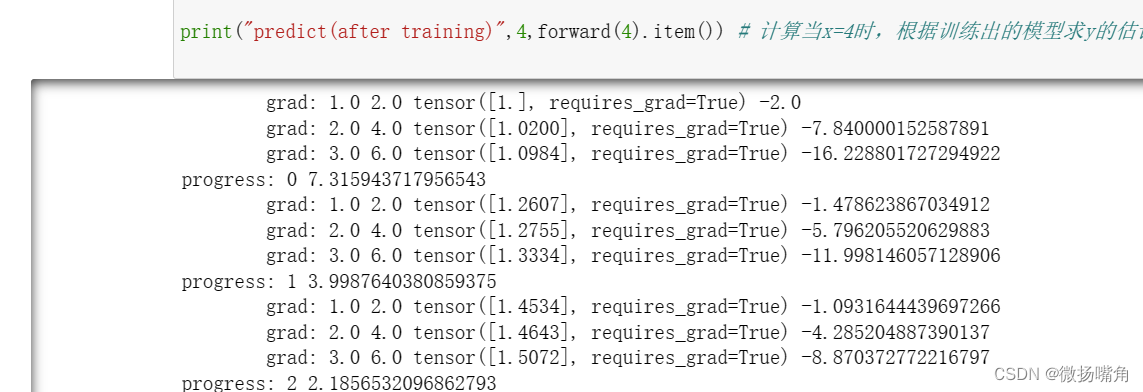
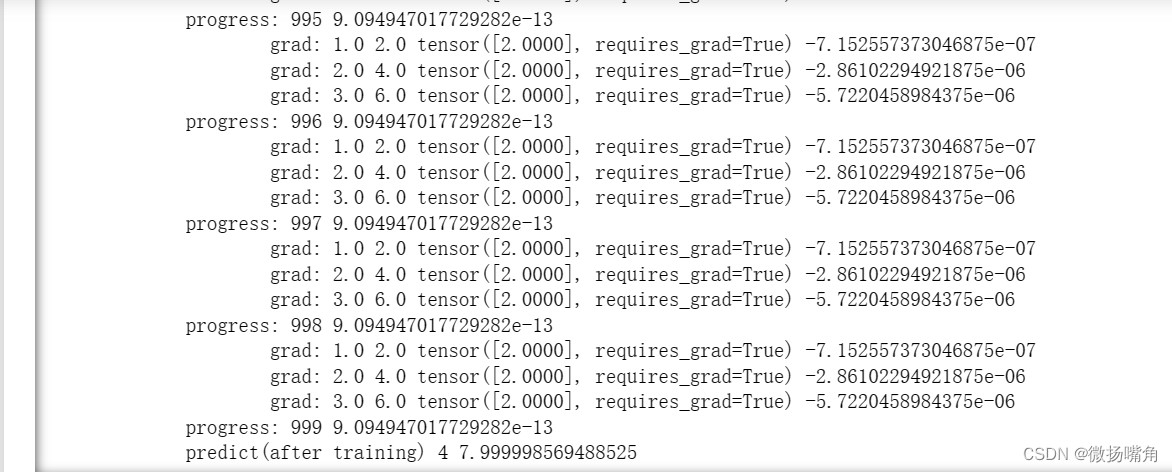
在这里插入图片描述

可以看出w的值一直在增加，直到加到2可以完全拟合训练集中x与y的关系，最后当x等于4时，估计值接近8.

二、神经网络
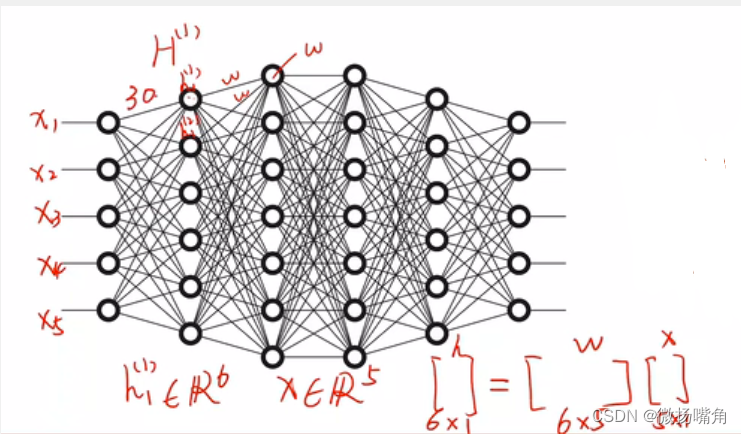
在这里插入图片描述
我们知道，神经网络由多层组成，包括输入层、隐含层和输出层，每一层的包含不同个数的结点，每层的结点其实就是当前我们获得的数据的特征值（features），例如输入层（x1,x2,x3,x4,x5）有五个结点分别表示五个特征值，第一层的隐藏层有六个结点，这是就需要一个6 * 5的矩阵w将x的5个特征值转变为6个特征值。当然也可以添加偏置值b如下图所示:
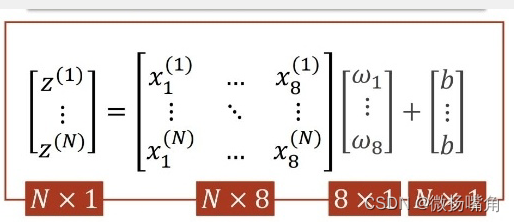
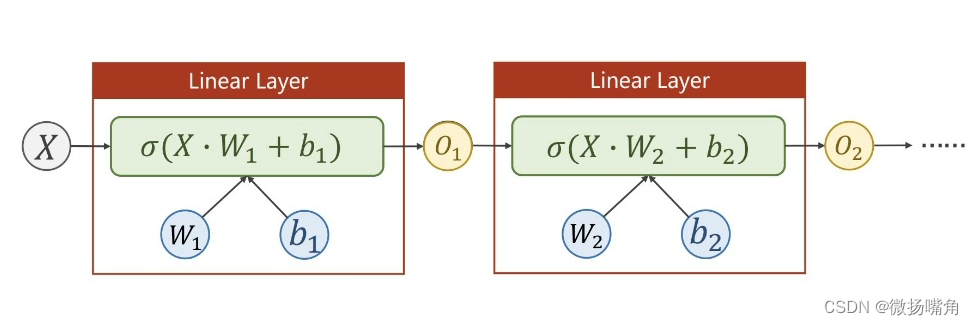
在这里插入图片描述

而这个矩阵w就是我们要训练出包含着某种关系的参数矩阵，再一层一层的变换，每层都有一个参数矩阵，最终到达输出矩阵的四个特征，即(y1,y2,y3,y4)。
为了是我们的神经网络模型更好地拟合非线性函数关系，还可以使用激活函数：
在这里插入图片描述
激活函数前面的文章讲过，这里不再说了。使用sigmoid激活函数如下：

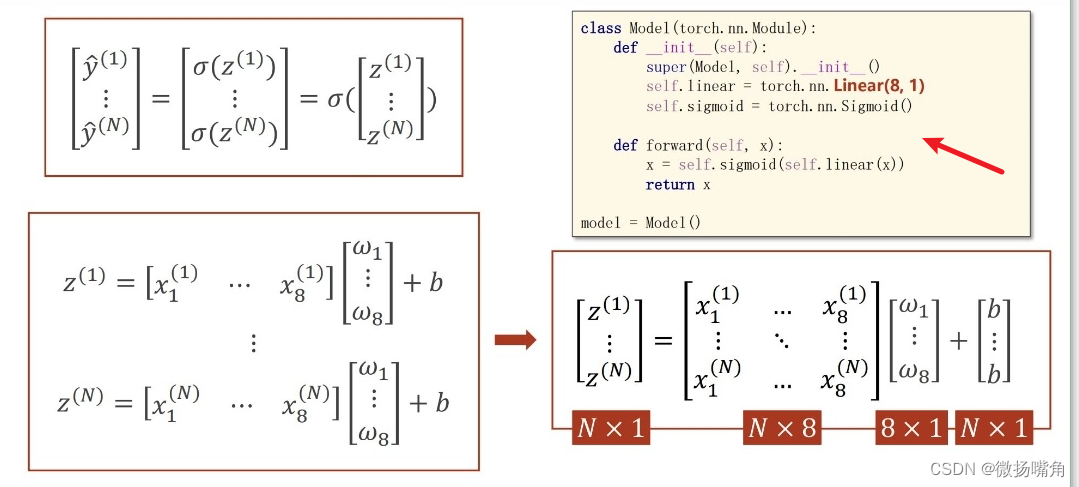
代码实现：
1.单隐藏层的神经网络模型
pytorch对于神经网络的代码封装得很好。

# 训练数据集
x_data = torch.tensor([[1.0],[2.0],[3.0]])
y_data = torch.tensor([[2.0],[4.0],[6.0]])

# 定义一个单隐藏层得神经网络
class LinearModel(torch.nn.Module):# 神经网络的类必须继承类Module
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1,1) # torch.nn.Linear(1,1)表示该神经网络处理的是n * 1的输入，输出也是n * 1。
        # torch.nn.Linear()第三个参数是bias，设置为True即含有偏置值b，为False不适用偏置值，默认值为True。
        
    def forward(self,x):
        y_pred = self.linear(x) # 使用封装好的linear()计算y的预测值
        return y_pred

# 生成神经网络的模型
model = LinearModel()

# 损失函数
criterion = torch.nn.MSELoss(size_average=False) # size_average=False表示损失函数不求平均值

# 优化器（梯度下降）
optimizer = torch.optim.SGD(model.parameters(),lr=0.01) # model.parameters()可以获取神经网络中的所有参数参数矩阵的值，对其进行优化
# lr表示步长
        
# 训练数据集
for epoch in range(100):
    y_pred = model(x_data) # 将数据传入搭建好的神经网络模型得到估计值
    loss = criterion(y_pred,y_data) # 计算损失值
    print(epoch,loss)
    optimizer.zero_grad() # 清除上次的梯度值
    loss.backward() # 自动求导
    optimizer.step() # 优化参数
    
# 输出结果
print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())

# 测试模型
x_test = torch.tensor([4.0])
y_test = model(x_test)
print('y_pred=',y_test.data)

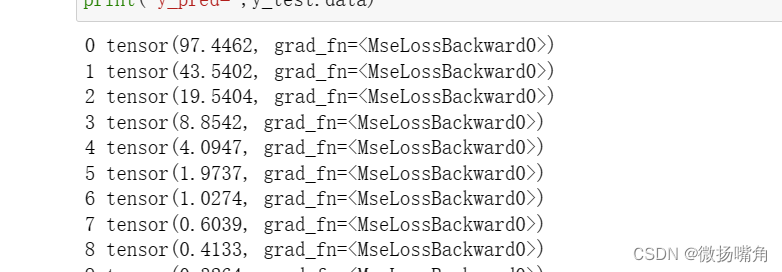
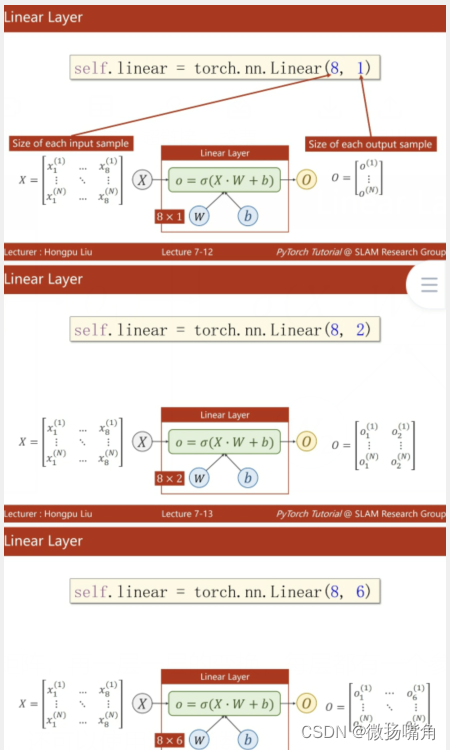
在这里插入图片描述

说明：这里的torch.nn.Linear(1,1)表示该神经网络处理的是n * 1的输入，输出也是n * 1，其它情况使用情况如下：

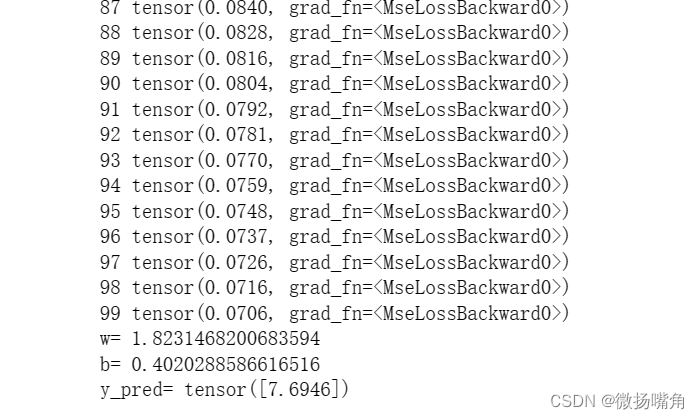
可以看出，训练100轮效果不佳，可以训练1000次看看不同结果。

2.多隐藏层的神经网络模型
与单隐藏层神经网络模型区别如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model,self).__init__()
        self.linear1 = torch.nn.Linear(8,6) # 模型从8维变为6维，再从6维变为4维，再从4维变为1维
        self.linear2 = torch.nn.Linear(6,4)
        self.linear1 = torch.nn.Linear(4,1)
        self.sigmoid = torch.nn.Sigmoid() # 使用sigmoid激活函数
        
    def forward(self,x):
        pred1 = self.sigmoid(self.linear1(x)) # 上一层输出结果传给下一层
        pred2 = self.sigmoid(self.linear2(pred1))
        y_pred = self.sigmoid(self.linear3(pred2))
        return n
    
model = Model()