最近在刷力扣时遇见的问题，自己总结加上看了力扣大佬的知识总结写下本篇文章，我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题，是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些，如果没有掌握一定的方法，DFS 代码容易写得冗长繁杂。

1.1网格问题基本概念

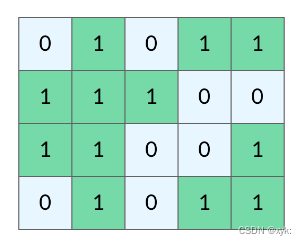
网格问题是由 m×n 个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。 数字为1的格子连接起来就形成一个岛屿。

 1.2 DFS的基本结构

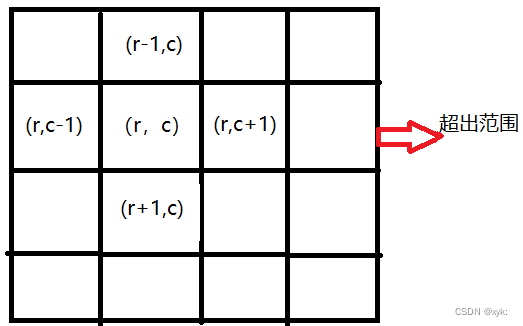
首先我们要确定访问的下一个节点以及停止的边界，那么首先网格结构中的每个格子可以向四周延伸，分别为上，下，左，右，对于格子(r,c)来说，对应的四个坐标分别为(r+1,c)、(r-1,c)、(r,c-1)、(r,c+1)。

 

 其次超出格子的边界是什么?是grid[r][c]出现下标越界异常的格子，也就是那些超出范围的格子。

 

 这样我们就得到了网格DFS遍历的框架代码：

public void infect(char[][] grid,int i ,int j){
//超出范围
        if (i < 0 || i >= grid.length || 
        j < 0 || j >= grid[0].length){
            return;
        }
//访问上，下，左，右
        infect(grid,i+1,j);
        infect(grid,i-1,j);
        infect(grid,i,j+1);
        infect(grid,i,j-1);
}

1.3 如何避免重复遍历

网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。这是因为，网格结构本质上是一个「图」，我们可以把每个格子看成图中的结点，每个结点有向上下左右的四条边。在图中遍历时，自然可能遇到重复遍历结点。

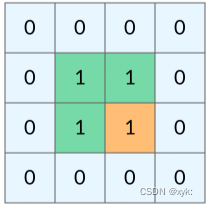
 如何避免这样的重复遍历呢？答案是将已经遍历过的格子的值修改一下，每次走过一个格子就修改格子的值。以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。

public void infect(char[][] grid,int i ,int j){
        if (i < 0 || i >= grid.length || 
        j < 0 || j >= grid[0].length ){
            return;
        }
        grid[i][j] = '2';
        infect(grid,i+1,j);
        infect(grid,i-1,j);
        infect(grid,i,j+1);
        infect(grid,i,j-1);
    }

二、岛屿经典例题

2.1 岛屿数量

岛屿类问题的通用解法、DFS 遍历框架 - 岛屿数量 - 力扣（LeetCode）

• 0 —— 海洋格子
• 1 —— 陆地格子（未遍历过）
• 2 —— 陆地格子（已遍历过）

class Solution {
   public int numIslands(char[][] grid) {
        int islandNum = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1'){
                    infect(grid,i,j);
                    islandNum++;
                }
            }
        }
        return islandNum;
    }
    
    public void infect(char[][] grid,int i ,int j){
        if (i < 0 || i >= grid.length || 
        j < 0 || j >= grid[0].length || grid[i][j] != '1'){
            return;
        }
        grid[i][j] = '2';
        infect(grid,i+1,j);
        infect(grid,i-1,j);
        infect(grid,i,j+1);
        infect(grid,i,j-1);
    }
}

2.2 岛屿的周长

463. 岛屿的周长 - 力扣（LeetCode）

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

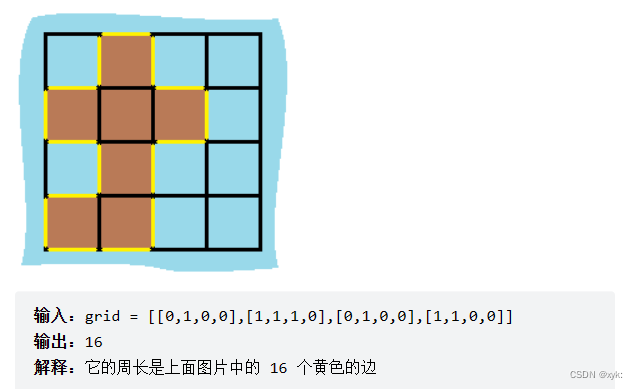
我们可以将岛屿的周长中的边分为两类，如下图所示。黄色的边是与网格边界相邻的周长，而蓝色的边是与海洋格子相邻的周长。

当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候，实际上就经过了一条黄色的边；而当函数因为「当前格子是海洋格子」返回的时候，实际上就经过了一条蓝色的边。

 本题我们可以再次嵌套DFS的框架，但是要增加几处地方，实际上，岛屿的周长是计算岛屿全部的「边缘」，而这些边缘就是我们在 DFS 遍历中，dfs 函数返回的位置。

class Solution {
    public int islandPerimeter(int[][] grid) {
        for (int r = 0; r < grid.length; r++) {
            for (int c = 0; c < grid[0].length; c++) {
                if (grid[r][c] == 1){
                    return dfs(grid,r,c);
                }
            }
        }
        return 0;
    }

    public int dfs(int[][] grid,int r,int c){
        if (r < 0 || r >= grid.length ||
                c < 0 || c >= grid[0].length ){
            return 1;
        }
        if (grid[r][c] == 0){
            return 1;
        }
        if (grid[r][c] != 1){
            return 0;
        }
        grid[r][c] = 2;
        return dfs(grid,r-1,c)+dfs(grid,r+1,c)
                +dfs(grid,r,c-1)+dfs(grid,r,c+1);
    }
}

2.3 单词搜索

79. 单词搜索 - 力扣（LeetCode）

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

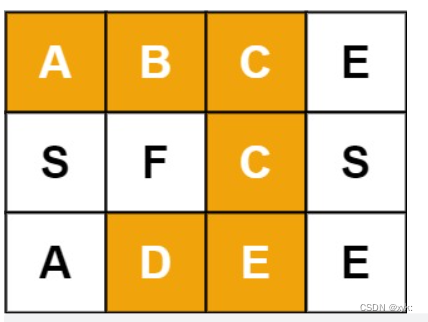
 本题在使用上面的DFS框架时，要加上回溯，因为当搜索一次时，会更改当前的格子的值，

如果我在DFS的过程中不改矩阵的状态，那我就会出现重复搜索的情况啊，这可不行，因此矩阵是必须得改的。那就只剩下一个办法了，每次DFS的过程中修改矩阵，DFS完了再把矩阵给改回去呗，这就是回溯！

那么什么是剪枝呢？所谓剪枝就是我在dfs的时候，如果已经找到一个正确的路径了，换句话说已经得到结果了，其实就没必要继续DFS了，直接返回结果即可。这就是剪枝。

给一下官方的说法：剪枝，就是减小树的规模，尽早排除搜索树中不必要的分支的一种手段。

class Solution {
    private boolean find;
    public boolean exist(char[][] board, String word) {
        if(board == null){
            return false;
        }
        int m = board.length,n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        find = false;

        for(int i = 0;i < m;i++){
            for(int j = 0 ;j < n;j++){
                backtracking(i, j, board, word, visited, 0);
            }
        }
        return find;
    }

    /**
    * i,j,board：棋盘格及当前元素的坐标
    * word: 要搜索的目标单词
    * visited：记录当前格子是否已被访问过
    * pos: 记录目标单词的字符索引，只有棋盘格字符和pos指向的字符一致时，才有机会继续搜索接下来的字符；如果pos已经过了目标单词的尾部了，那么便说明找到目标单词了
    */
    public void backtracking(int i, int j, char[][] board, String word, boolean[][] visited, int pos){
         // 超出边界、已经访问过、已找到目标单词、棋盘格中当前字符已经和目标字符不一致了
        if(i < 0 || i >= board.length || j <0 || 
        j>=board[0].length || visited[i][j] || 
        find || board[i][j] != word.charAt(pos)){
            return;
        }
        if(pos == word.length()-1){
            find = true;
            return;
        }

        visited[i][j] = true;// 修改当前节点状态
        backtracking(i+1, j, board, word, visited, pos+1);  // 遍历子节点
        backtracking(i-1, j, board, word, visited, pos+1);
        backtracking(i, j+1, board, word, visited, pos+1);
        backtracking(i, j-1, board, word, visited, pos+1);
        visited[i][j] = false; // 撤销修改
    }
}

如果对你有帮助，麻烦双击三连一下，谢谢啦！