作者：学Java的冬瓜
博客主页：☀冬瓜的主页🌙
专栏：【C/C++数据结构与算法】
分享：那我便像你一样，永远躲在水面之下，面具之后！ ——《画江湖之不良人》
主要内容：八大排序选择排序中的冒泡排序、选择排序(递归+非递归)，理解快速排序一趟排序的三种算法：挖坑法，左右指针法，前后指针法。还有关于快排优化：三数取中法，小区间优化。

在这里插入图片描述

文章目录

一、冒泡排序
- 1. 思路
- 2. 复杂度
- 3. 代码
二、快速排序
- 1. 思路：
- - 方法：挖坑法、左右指针、前后指针
  - 优化操作：三数取中法、小区间优化
- 2. 复杂度
- 3. 代码
- - 3.1 挖坑法左右指针前后指针(一趟排序)
  - 3.2 三数取中小区间优化递归实现排序
- 4. 补充：测试排序性能方法
- 5. 补充：快排非递归

一、冒泡排序

1. 思路

理解：这是排序中几乎最简单的一个排序。比如要把一组数从小到大排序，就是依次比较两数大小，大的数往后挪，直到最大数放在最后面这就完成了一次冒泡。然后最后边界减一，和之前一样的操作，直到完成n-1次冒泡。最重要的是：注意边界下标的控制！

2. 复杂度

时间复杂度：O(N^2)
如果使用优化版(使用一个变量标记在一趟排序中是否发生了交换，不发生交换，则表示这组数据刚好符合排序要求)，且这组数刚好是按照要求，从小到大排的（和示例代码一致），那么时间复杂度达到O(N)

3. 代码

// 冒泡排序1(优化版)
// 时间复杂度：O(N^2)
void BubbleSort(int* arr, int size)
{
	for (int i = 0; i < size - 1; i++) {
		int exchange = 0;
		for (int j = 1; j < size - i; j++) {
			if (arr[j - 1] > arr[j]) {
				Swap(&arr[j - 1], &arr[j]);
				exchange = 1;
			}
		}
		if (exchange == 0) {
			break;
		}
	}
}

// 冒泡排序2
void BubbleSort(int* arr, int size)
{
	// 利用end控制末尾边界
	int end = size;
	while (end > 0) {
		for (int j = 1; j < end; j++) {
			if (arr[j - 1] > arr[j]) {
				Swap(&arr[j - 1], &arr[j]);
			}
		}
		end--;
	}
}

二、快速排序

1. 思路：

方法：挖坑法、左右指针、前后指针

挖坑法：随机或者选择开头第一个数做key，把右边比key小的数挪到左边，把左边比key大的数挪到右边，这样就找到了key的位置(即把key放入了该放的位置)，然后左右在分【left，key-1】 key 【key+1，right】的区间去递归找到并放入每一个数到排序中该放的数。
左右指针：begin下标从左找比key大的数，end下标从右找比key小的数，然后交换位置，直到begin遇到end，和挖坑法很相似。
前后指针：cur下标在前，prev下标紧跟其后从左到右搜索。cur下标找到比key小的数时，先prev++，然后 Swap(&a[prev]，a[cur]) ；会有两种情况：其一：cur就在prev后一个，prev++后赋值，是自己给自己赋值。其二：cur和prev之间隔着大于key的数，交换就是把cur下标所在的这个比key小的数和prev与cur之间比key大的数交换。结局就是比key小的数放在了前面，大的数移到了后面。

优化操作：三数取中法、小区间优化

三数取中法对有序的有大量数据的数组很有作用，可以大大加大快速排序的效率。
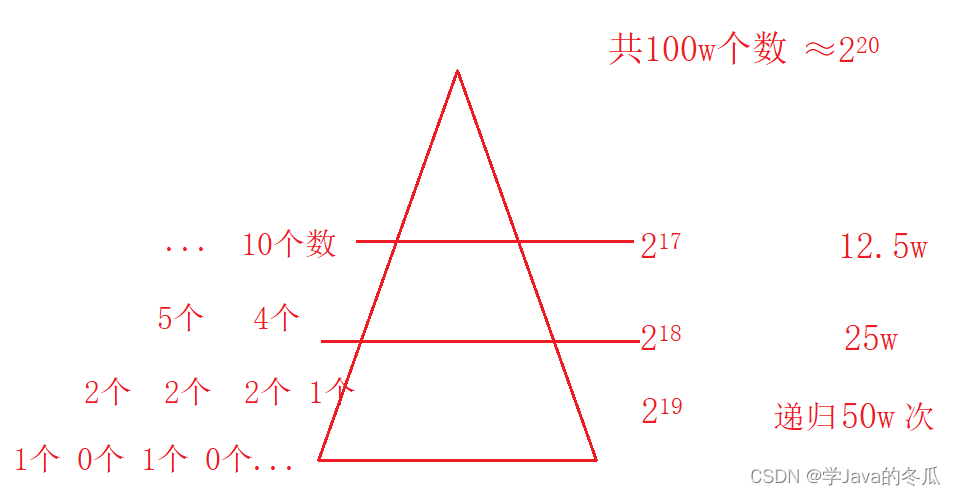
小区间优化目的是：减少函数递归，从而减少栈帧的创建和销毁，提高效率，但是一般不是很明显。比如对长度100w的数组排序，最后三层就占了87.5w次递归。

2. 复杂度

时间复杂度：O(NlogN)。每次挖坑后区间减半，分两边去操作，一共需要排序N个数据，所以，需要选择key共logN次，每个数找它的位置时，要遍历整个数组(长度为N)。所以复杂度为O(NlogN)。

3. 代码

3.1 挖坑法左右指针前后指针(一趟排序)

// 一趟排序
// 法一：挖坑法
int FuncPart1(int* a, int left, int right)
{
	// 三数取中法
	int mid = getMidIndex(a + left, right - left + 1);
	Swap(&a[left], &a[left + mid]);  // 注意范围理解

	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];

	// 1、排序一趟的操作
	while (begin < end)
	{	// 2、右边找小
		while (begin < end && key <= a[end])  // 要加上begin<end的条件，如果从外面的while进入后，
			end--;                                 // 内层的while不判断就操作，会导致begin和end错开，从而出现错误排序
		//Swap(&a[pivot], &a[end]);  //注意：不能直接交换，不然交换时消耗大量时间就达不到快速的效果
		// 2.1、把坑位赋值为这个右边比key小的这个数，再更新坑位pivot
		a[pivot] = a[end];
		pivot = end;

		// 3、左边找大
		while (begin < end && a[begin] <= key)
			begin++;
		//Swap(&a[begin], &a[pivot]);   //注意：不能直接交换，不然交换时消耗大量时间就达不到快速的效果
		// 3.1、把坑位赋值为这个左边比key大的这个数，再更新坑位pivot
		a[pivot] = a[begin];
		pivot = begin;
	}

	// 4、把key这个数放进它的位置
	pivot = begin;
	a[begin] = key;

	return pivot;
}

// 法二：左右指针法
int FuncPart2(int* a, int left, int right)
{

	int mid = getMidIndex(a, right - left + 1);
	Swap(&a[left], &a[left + mid]);

	int begin = left;
	int end = right;
	int keyi = begin;

	while (begin < end) {
		// 找小
		while (begin < end && a[keyi] <= a[end]) {
			end--;
		}
		// 找大
		while (begin < end && a[begin] <= a[keyi]) {
			begin++;
		}
		Swap(&a[begin], &a[end]);
	}
	Swap(&a[begin], &a[keyi]);

	keyi = begin;
	return keyi;
}

// 法三：前后指针法
int FuncPart3(int* a, int left, int right)
{
	int mid = getMidIndex(a, right - left + 1);
	Swap(&a[left], &a[left + mid]);

	int prev = left, cur = left + 1;
	int keyi = left;

	while (cur <= right) {
		if (a[cur] < a[keyi] && ++prev != cur) { // 注解：1只要cur的值小于keyi的值，prev就自增，即prev要标记左边最后比keyi小的数。
			Swap(&a[prev], &a[cur]);           //      2当进入if时，prev刚好在cur的后一个时,就是cur自己赋值给自己。
		}
		++cur;
	}
	// 注意：退出循环时，prev下标的值是最后一个比keyi值小的数，所以交换二者后，keyi就找到它的位置。
	Swap(&a[keyi], &a[prev]);

	keyi = prev;
	return keyi;
}

3.2 三数取中小区间优化递归实现排序

// 三数取中
int getMidIndex(int* a, int n)
{
	int left = 0;
	int right = n - 1;
	int mid = (left + right) / 2;
	if (a[left] < a[mid]) {
		if (a[mid] < a[right]) {
			return mid;
		}
		//a[mid]>a[right]
		else if (a[left] < a[right]) { 
			return right;
		} 
		// a[left]<a[mid] a[mid]>a[right] a[left]>=a[right]
		else {
			return left;
		}
	}
	// a[left] >= a[mid]
	else {
		if (a[mid] > a[right]) {
			return mid;
		}
		// a[mid] < a[right]
		else if (a[right] > a[left]) {
			return left;
		}
		//a[left]>=a[mid] a[mid]<a[right] a[right]<=a[left]
		else {
			return right;
		}
	}
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int pivot = FuncPart3(a, left, right);
	 注意0：在数据量在一定范围内，无序情况下快排比堆排和希尔都快，但有序时，快排要慢很多。
	// 
	 分成区间[left,pivot-1] pivot [pivot+1,right]，递归去实现子区间有序
	//QuickSort(a , left, pivot - 1);
	//QuickSort(a , pivot + 1, right);


	// 小区间优化(n<=10,使用直接插入排序，但是这个方法优化效率不明显)
	if (pivot - 1 - left > 10) {
		QuickSort(a, left, pivot - 1);
	}
	else {
		InsertSort(a + left, pivot - 1 - left + 1);
	}
	if (right - (pivot + 1) > 10) {
		QuickSort(a, pivot + 1, right);
	}
	else {
		InsertSort(a + pivot + 1, right - (pivot + 1) + 1);
	}
}

4. 补充：测试排序性能方法

// 测试性能
void TestOP()
{
	// 使用malloc申请新的空间，那么第二个排序就不会收到第一个排序结果的影响。否则，如果只使用传入的数组，排完一次后就有序了，那么其它排序前，数组就已经有序了。
	srand(time(NULL));  // 产生随机数
	int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	int* a8 = (int*)malloc(sizeof(int) * N);


	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		//a1[i] = i;
		//a1[i] = N-i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
		a8[i] = a1[i];

	}

	long int begin1 = clock();  // 获取毫秒数
	InsertSort(a1, N);
	long int end1 = clock();

	long int begin2 = clock();
	ShellSort(a2, N);
	long int end2 = clock();

	long int begin3 = clock();
	SelectSort(a3, N);
	long int end3 = clock();

	long int begin4 = clock();
	HeapSort(a4, N);
	long int end4 = clock();

	long int begin5 = clock();
	BubbleSort(a5, N);
	long int end5 = clock();

	long int begin6 = clock();
	QuickSort(a6, 0, N - 1);
	long int end6 = clock();

	long int begin7 = clock();
	MergeSort(a7, N);
	long int end7 = clock();


	printf("直接插入：%ld ms\n", end1 - begin1);
	printf("希尔排序：%ld ms\n", end2 - begin2);
	printf("选择排序：%ld ms\n", end3 - begin3);
	printf("堆排序  ：%ld ms\n", end4 - begin4);
	printf("冒泡排序：%ld ms\n", end5 - begin5);
	printf("快速排序：%ld ms\n", end6 - begin6);
	printf("归并排序：%ld ms\n", end7 - begin7);
}

5. 补充：快排非递归

注意：对快排来说(不分递归非递归），逆序会比随机或者顺序慢很多，因为即使使用三数取中法，左右数字全都是需要交换的，复杂度虽然没有到O(N^2)，但比O(NlogN)大很多。
快速排序有了非递归，为什么还要实现非递归呢？非递归最根本的原因就是为了解决栈溢出的问题。排序的数据量很大时(比如1000w个数)，递归的深度会很深，栈帧开销过大，这会让只有十几兆的栈空间不够用，导致栈溢出。
下面的例子是借用数据结构的栈，来模拟实现快排。要看栈可以看这篇博客：栈和队列。
另外，快排非递归也可以利用队列来实现，利用先进先出的规则。比如4 2 9 5 1 3 8，忽略三数取中法，利用栈或队列如下：

// 非递归：
// 快速排序：
int FuncPart(int* a, int left, int right)
{
	 三数取中法
	int mid = getMidIndex(a + left, right - left + 1);
	Swap(&a[left], &a[left + mid]);  // 注意理解范围

	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];

	// 1、排序一趟的操作
	while (begin < end)
	{	// 2、右边找小
		while (begin < end && key <= a[end])  // 要加上begin<end的条件，如果从外面的while进入后，
			end--;                                 // 内层的while不判断就操作，会导致begin和end错开，从而出现错误排序
		//Swap(&a[pivot], &a[end]);  //注意：不能直接交换，不然交换时消耗大量时间就达不到快速的效果
		// 2.1、把坑位赋值为这个右边比key小的这个数，再更新坑位pivot
		a[pivot] = a[end];
		pivot = end;

		// 3、左边找大
		while (begin < end && a[begin] <= key)
			begin++;
		//Swap(&a[begin], &a[pivot]);   //注意：不能直接交换，不然交换时消耗大量时间就达不到快速的效果
		// 3.1、把坑位赋值为这个左边比key大的这个数，再更新坑位pivot
		a[pivot] = a[begin];
		pivot = begin;
	}

	// 4、把key这个数放进它的位置
	pivot = begin;
	a[begin] = key;

	return pivot;
}
void QurickSortNonR(int* a, int n)
{
	Stack st;
	StackInit(&st);
	StackPush(&st, n - 1);
	StackPush(&st, 0);
	while (!StackEmpty(&st)) {
		int left = StackTop(&st);
		StackPop(&st);

		int right = StackTop(&st);
		StackPop(&st);

		int Index = FuncPart(a, left, right);  // 用挖坑法，一趟排序

		// [left, index-1] index [index+1, right]
		// Push先入右，后入左，那Pop先出左
		if (Index + 1 < right) {  // 代表Index右边至少还有两数没排，继续入栈
			StackPush(&st, right);
			StackPush(&st, Index + 1);
		}
		if (left < Index - 1) {
			StackPush(&st, Index - 1);
			StackPush(&st, left);
		}
	}
}