1

A假设比较t次,由于换或不换,则必然有2^t种可能。又设有n个关键字,n!排列组合,则必然有2^t>=n!,带入n即可解出。
2

注意这里没有考虑于哨兵的比较,少了一次,所以按n*(n-1)/2可以解出比较次数是10,B
3

注意这里增量为4要比较完整,A
4

比较次数变成了nlog2n但是移动次数没有改变,还是n^2,所以时间复杂度还是O(n^2)
5

二分的越均匀速度越快,越有序速度越慢,所以A、D
6

从小到大排{11,18,23,68,69,73,93},从大到小排{93,73,69,68,23,18,11},要求最终位置元素可以作为枢纽,只有3、4可以,C
7


每趟都要确定至少1个最终位置的结果,D只有1个32满足

8

可以用队列来代替栈
。
在快速排序的过程中
,
通过一趟划分
,
可以把一个待排序区间分为两
个子区间
,
然后分别对这两个子区间施行同样的划分
。
栈的作用是在处理一个子区间时
,
保存另
一个子区间的上界和下界(排序过程中可能产生新的左
、
右子区间)
,待该区间处理完后再从栈

中取出另一子区间的边界
,
对其进行处理
。
这个功能用队列也可以实现
,
只不过处理子区间的顺
序有所变动而已
。
9

int kth_elem(int low,int high,int k){
int pivot=num[low];
int low_t=low;
int high_t=high;
while(low<high){
while(low<high && pivot<=num[high]) high--;
num[low]=num[high];
while(low<high && pivot>=num[low]) low++;
num[high]=num[low];
}
num[low]=pivot;
if(low==k){
return num[low];
}else if(low<k){
return kth_elem(low+1,high_t,k);
}else if(low>k){
return kth_elem(low_t,low-1,k);
}
}void flag(int a[],int n){
int i=0,j=0,k=n-1;
while(j<=k){
switch(a[j]){
case red:swap(a[i],a[j]);i++,j++;break;
case white:j++;break;
case blue:swap(a[j],a[k]);k--;
}
}
cout<<i<<' '<<k<<endl;
for(int m=0;m<n;m++){
if(m<i) cout<<red<<' ';
else if(i<=m && m<=k) cout<<white<<' ';
else{
cout<<blue<<' ';
}
}
}int best_meet(int n){
int low=0,high=n-1;
int low_t=low;
int high_t=high;
int k=n/2;
bool flag=false;
while(!flag){
int pivot=num[low];
while(low<high){
while(low<high && pivot<=num[high]) high--;
num[low]=num[high];
while(low<high && pivot>=num[low]) low++;
num[high]=num[low];
}
num[low]=pivot;
if(low==k-1){
flag=true;
}else if(low<k){
low_t=++low;
high=high_t;
}else if(low>k){
low=low_t;
high_t=--high;
}
}
int s1=0,s2=0;
for(int i=0;i<k;i++) s1+=num[i];
for(int i=k;i<n;i++) s2+=num[i];
return s2-s1;
}
10



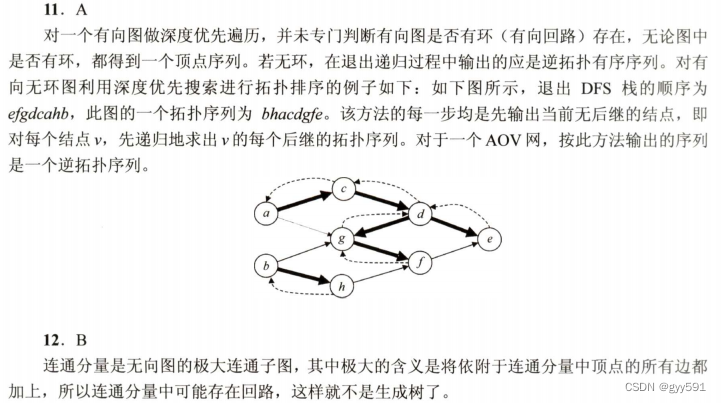
11


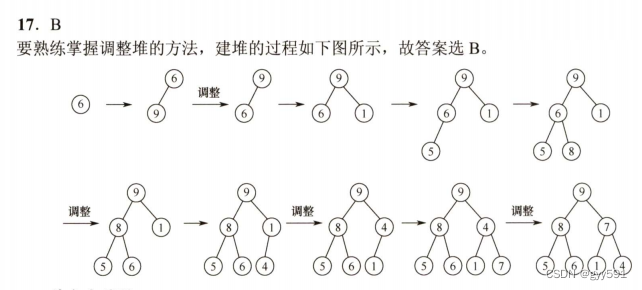
17B,注意是逐个插入,随时调整
12



13

![]()

14


0
15


16

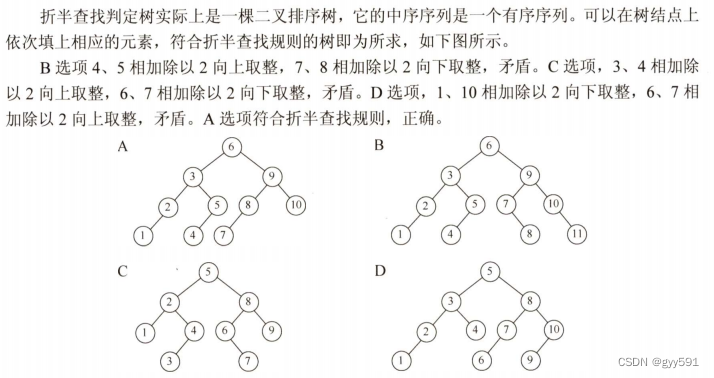
A 折半查找路径是一颗二叉排序树
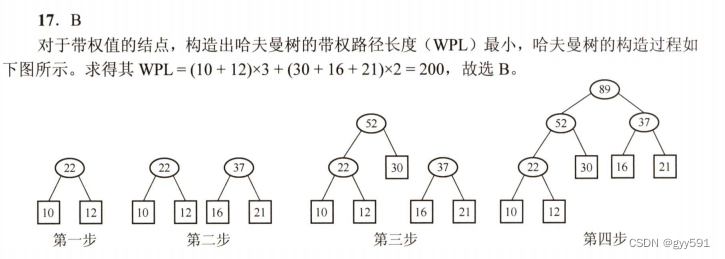
17

18


注意是空间复杂度

19


20


21


22

A,辅助空间都是O(1)无差
23



24

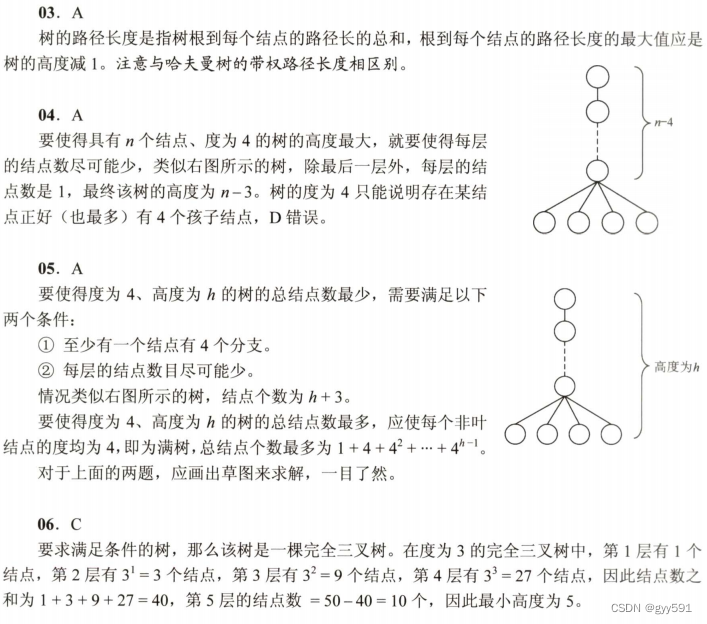



25







26


![]()



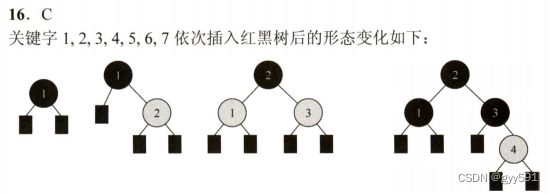


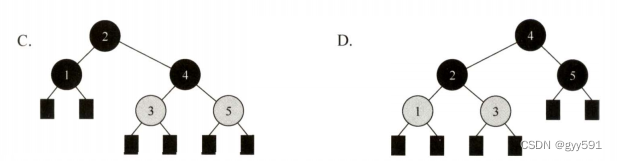
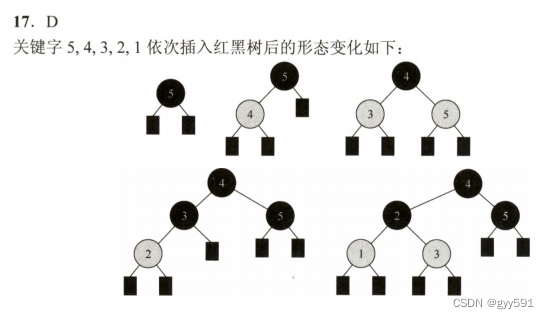

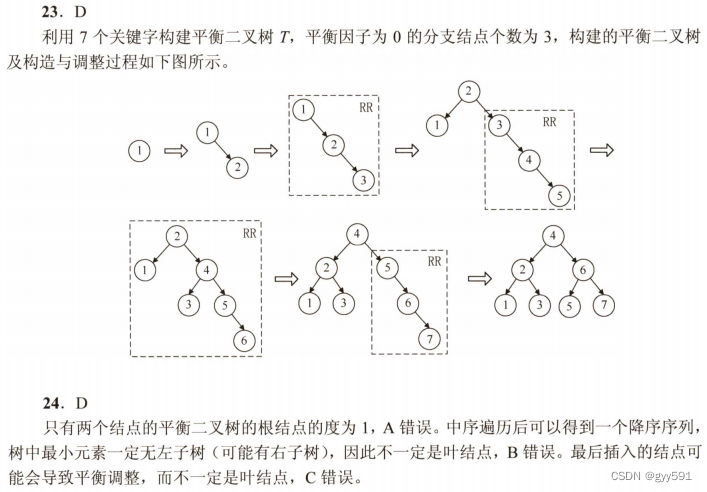
23中根节点也算分支节点


27






28



![]()









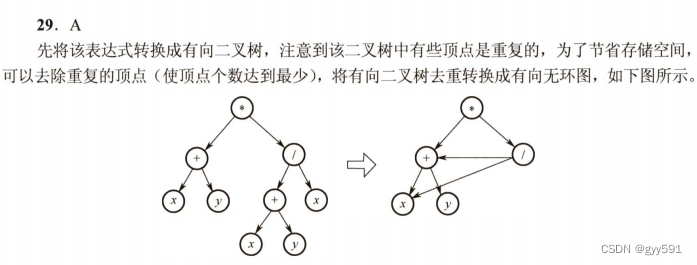
29
![]()
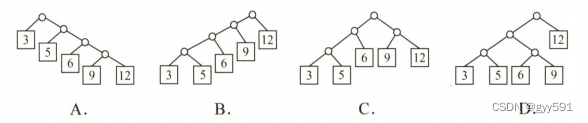








注意不是二叉树了


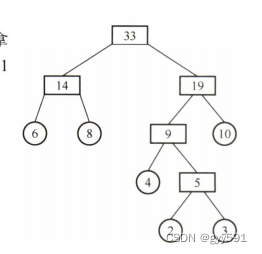
30
![]()






31




32






33







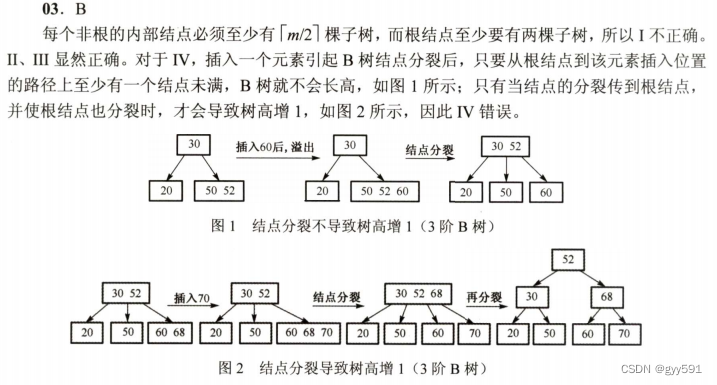




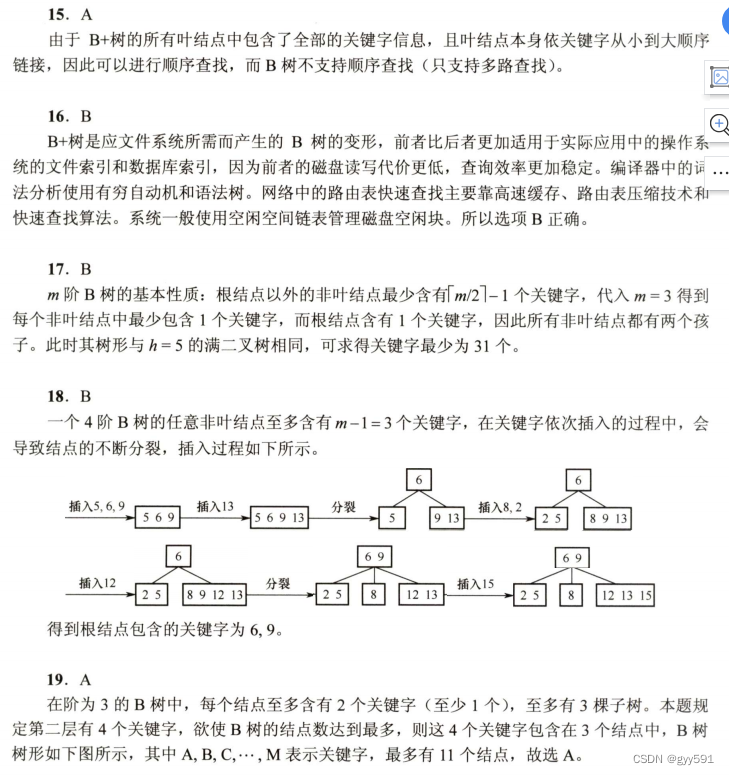

33





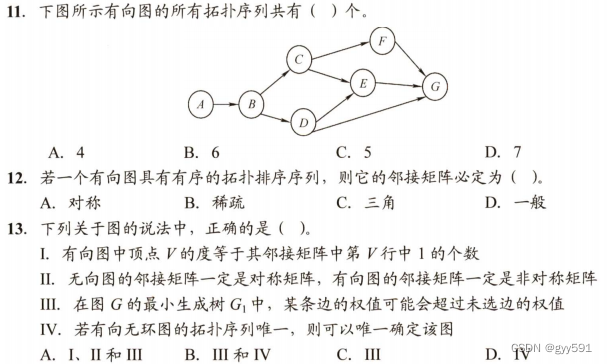

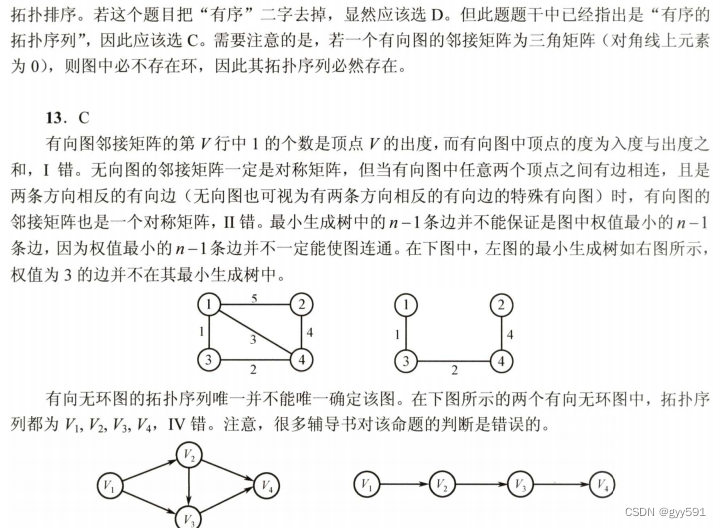



34







![]()