一、前言
目前在大量的灰度图像测试下,基本确定变换系数ratio取值0-25之间时,逆变化后的图还能基本保障效果,而且越接近0效果越好。本文还是以lenna.bmp灰度图为例,实验不再逆变换,而是把变换后的数据直接输出为bmp的灰度值,通过观察变换后的图像,思考两个问题:
1、从变换后的图可以看出我的变换算法与 DCT变换、小波变换是完全不同的,这里大家可以参考小波图像处理和 DCT图像处理(也可以参考 图像DCT变换),这里就不再把lenna.bmp在小波和DCT变换后的图重复贴出来。
2、设定ratio变换后通过统计和分析,给出变换后各个字节值的统计值以及对应的直线散点图,找出针对变换后的规律以及思考压缩方案。
二、不同变换参数下的图例
(2.1)ratio = 5
实验方法是不进行逆变换,直接把变换后的字节输出为bmp的灰度值,也可以理解为频谱信息如下:

从这个图不难看出,通过我的变换算法变换后是和DCT、小波完全不同的结果。
DCT变换的频谱信息如下:

小波变换的频谱信息如下:

显然,与DCT和小波变换是完全不同的,而且无法通过频谱信息得出有效的结论,所以只能从统计的角度给出各个符号出现的概率。
(2.2)ratio = 10,15,20
下图为ratio = 10

下图为ratio = 15

下图为ratio = 20

通过实验,我们能得到的唯一结论就是,频谱信息越来越白,这就是为什么前面的实验我一直都是以统计0xFF的数量来分析的。
三、不同变换参数下各字节统计值的散点图
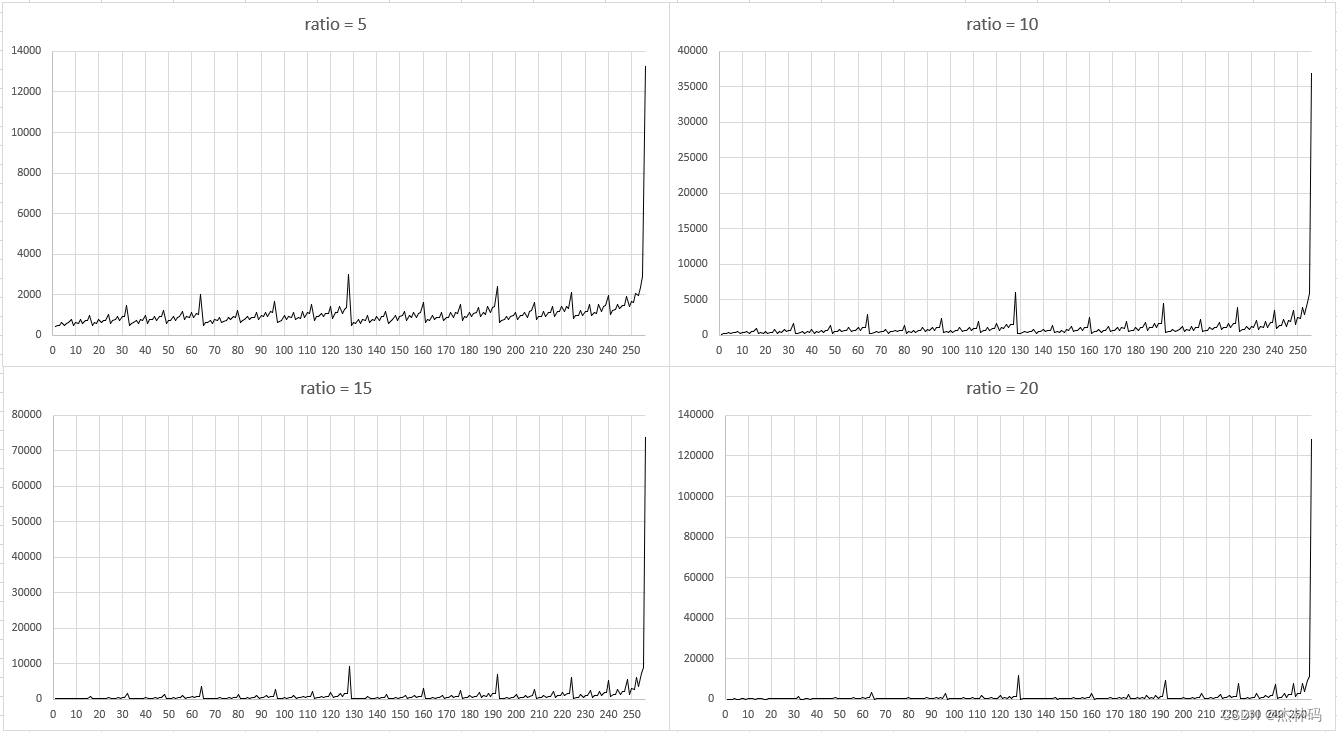
不难得出,各个值的统计特征基本相同,而且0xFF、0x80,0xC0,0xE0以及其他的几个特殊的值会大量出现,但是各个字节出现的位置是随机的,不确定的。所以我的变换算法最适合采用类似哈夫曼编码、算术编码类的方式进行压缩,即不同的字节值根据概率给定不同的码字,以ratio=20为例,0xFF共有128384,如果分配的码字为1,那么利用哈夫曼编码至少可以压缩到16048个字节。
当然,从优化的角度来讲,也可以以行为单位,或块为单位变换,这个将放在后面作为图像压缩和视频压缩的优化方案中。
接下来,我会采用加权概率模型的熵编码进行压缩实验。