前言

在本科毕设结束后，我开始刷卡哥的“代码随想录”，每天一节。自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。
代码随想录此题链接

题目

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

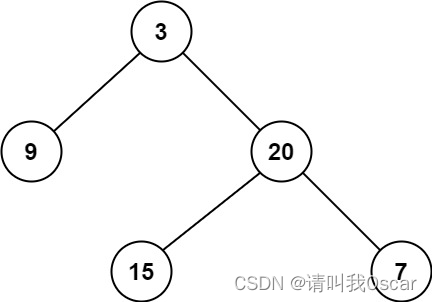
在这里插入图片描述

返回它的最大深度 2。

1.层序迭代

思路

层序遍历所有节点，设置一个记录层数int类型的参数，当遍历一层，此参数+1。
当发现遍历时存在左右孩子均为空的节点（叶子节点），说明当前层就是最小深度
二叉树层序遍历实现思路（使用一个队列(ArrayDeque实现)），两层循环，第一层（最外面那层）负责判断层级有没有遍历完（如果ArrayDeque为空则说明已经遍历完毕），第二层负责将本层的节点遍历完（提前申明一个size值用来记录本层的节点数，只遍历本层的这些节点），并且将下一层节点加入到队列中。（判断当前节点的左右孩子是否为空，若不为空则加入到ArrayDeque中）

2. 本题思路分析：

本题使用层序迭代

3. 算法实现

代码：
层序迭代：

public int minDepth(TreeNode root) {
   if(root == null){
       return 0;
   }
   Deque<TreeNode> nodes = new ArrayDeque<>();
   nodes.offer(root);
   int minDepth = 0;
   while(!nodes.isEmpty()){
       int size = nodes.size();
       for(int i = 0;i < size;i++){
           TreeNode cur = nodes.poll();
           if(cur.left == null && cur.right == null){
               return minDepth + 1;
           }
           if(cur.left != null){
               nodes.offer(cur.left);
           }
           if(cur.right != null){
               nodes.offer(cur.right);
           }
       }
       minDepth++;
   }
   return minDepth;
}