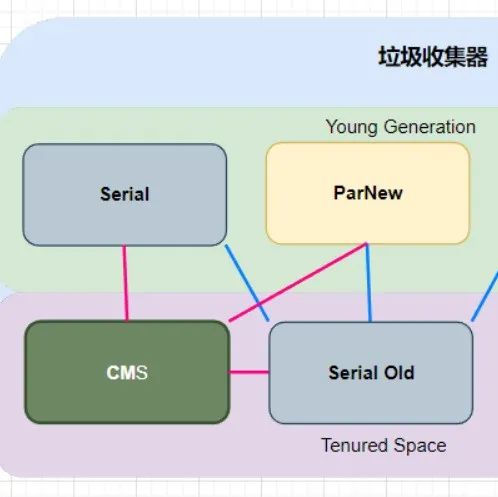
在分类问题中，尤其是在神经网络中，交叉熵函数非常常见。因为经常涉及到分类问题，需要计算各类别的概率，所以交叉熵损失函数与sigmoid函数或者softmax函数成对出现。

1.softmax                

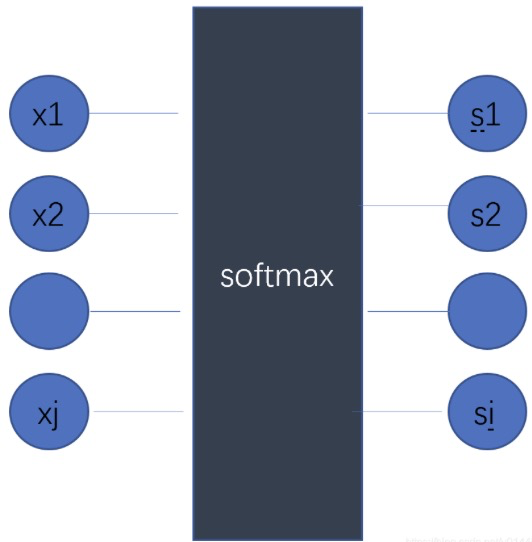
        softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内的概率，进行多分类。

        假设一个数组V，一共有j个元素Vi表示V中的第i个元素，第i个元素的softmax值公式如下。     

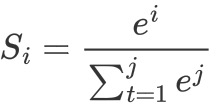
        softmax和交叉熵结合，因为交叉熵的输入是概率，而softmax就可以把网络的输出变成对应等比例的概率。

2.交叉熵损失函数(Cross Entropy Error Function)

        1. 二分类的交叉熵损失函数形式

         2.多分类的交叉熵损失函数形式

3.softmax 求导

3-1 求 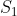对x1的导数 

 3-2 求 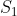对x2的导数 

        特别注意：因为在计算softmax时候，分母中用到了所有的X，分母包括了，，……，​​​​​​​，所以任何一个输出节点 都要对所有x 进行求导。以求 s1 对 x2 的导数为例，过程如下

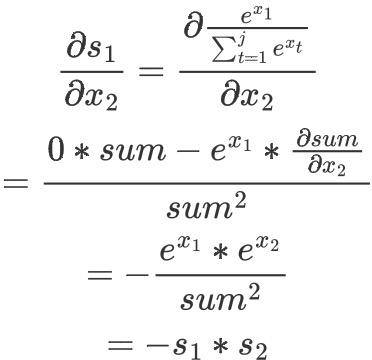
 3-3 softmax 的导数

        所以可以得到，i=j 时 和 i 不等于 j 时的 softmax导数。

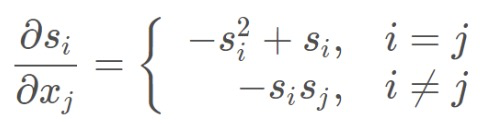
        注意区分：i是softmax之后得到s的下标，j是进入softmax之前x的下标，注意区分，可以看3-1和3-2的实例进行理解。 

4.softmax和交叉熵损失

4-1 计算过程

        分类任务中搭建神经网络时，交叉熵损失函数经常与softmax配合使用，假设有以下三个向量。

        向量𝑦(为one-hot编码,只有一个值为1,其他的值为0)真实类别标签(维度为𝑚,表示有𝑚类别)：

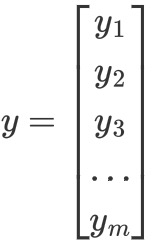
         向量𝑧为softmax函数的输入，和标签向量𝑦的维度一样，为𝑚：

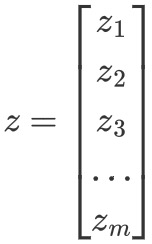
           向量𝑠为softmax函数的输出，和标签向量𝑦的维度一样，为𝑚：

        交叉熵损失函数具体计算公式如下

           损失函数对向量𝑧z中的每个𝑧𝑖求偏导： ​​​​​​​ 

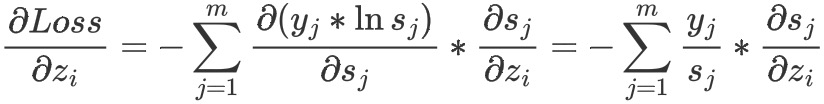
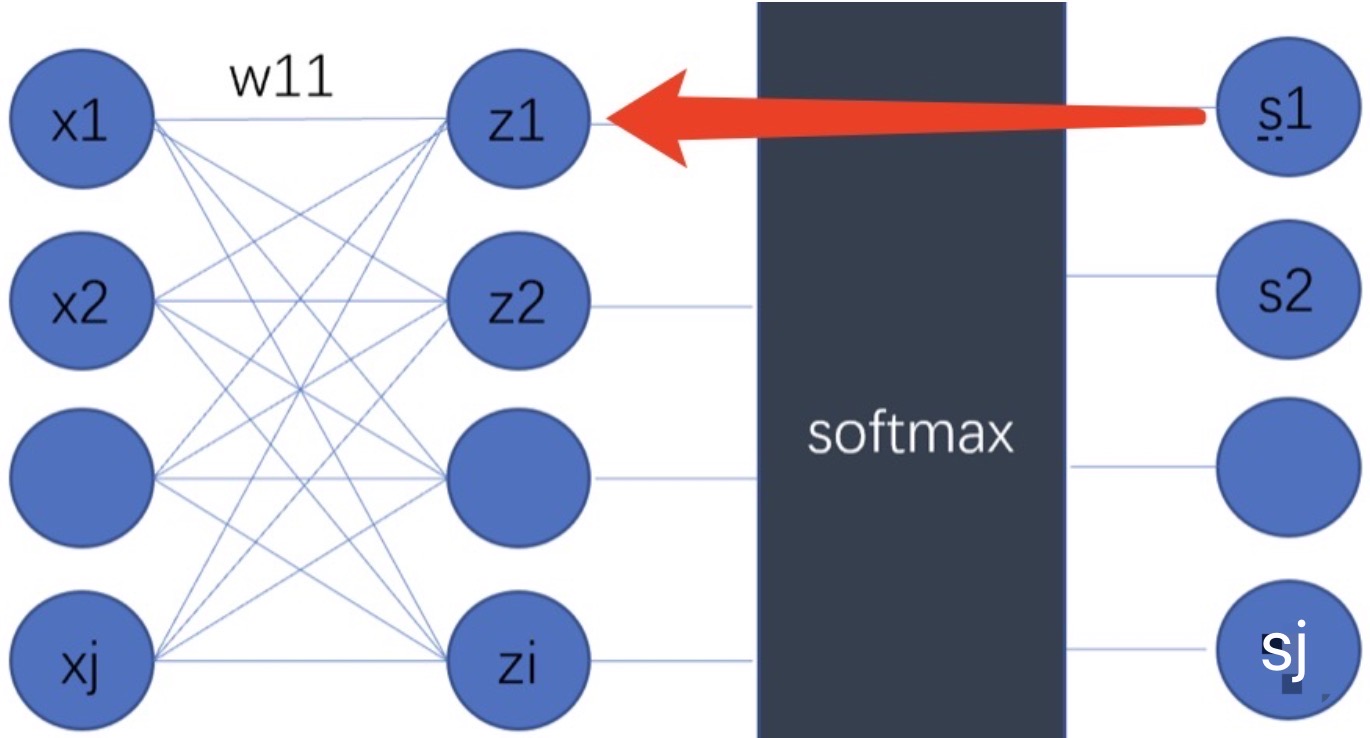
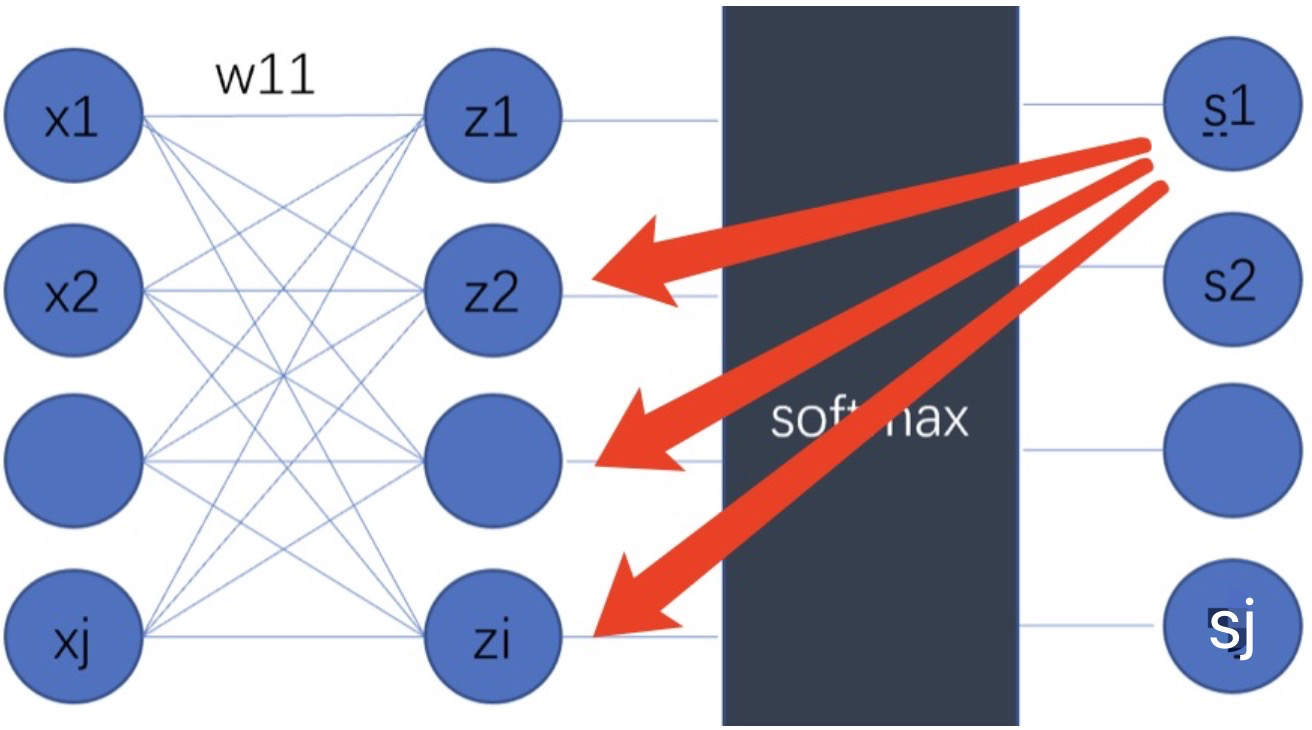
          需计算i等于j和i不等于j的加和，最后的计算结果如下：

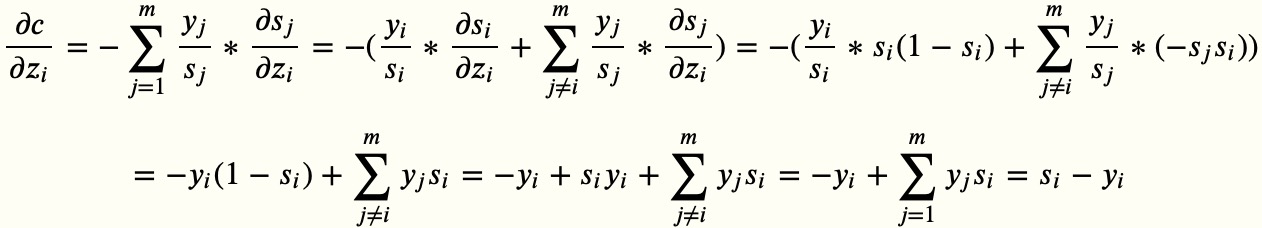
 4-2 实例

        通过计算最后得到的某个训练样本的向量的分数是[1,2,3], 经过softmax函数作用后

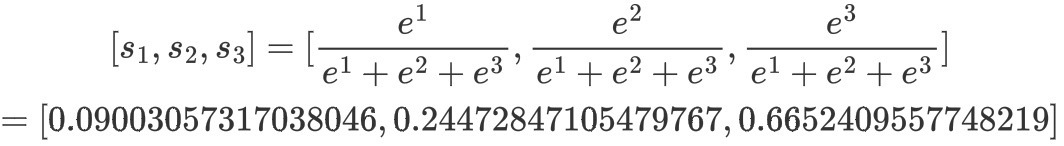
         假设正确的分类结果是那么计算出来的偏导就是（保留三位有效数字）[0.090-0，0.245-1，0.665-0]=[0.090，-0.755，0.665]。

        由计算结果可见，softmax和交叉熵结合之后求导，就是softmax之后的结果减去对应的y值，由此进行反向传播。 

Reference

        1.https://www.cnblogs.com/smallredness/p/11047718.html

        2.安全验证 - 知乎