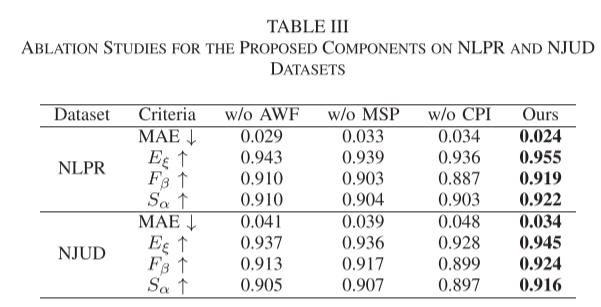
删除二叉搜索树中的节点
链接
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
示例 1:
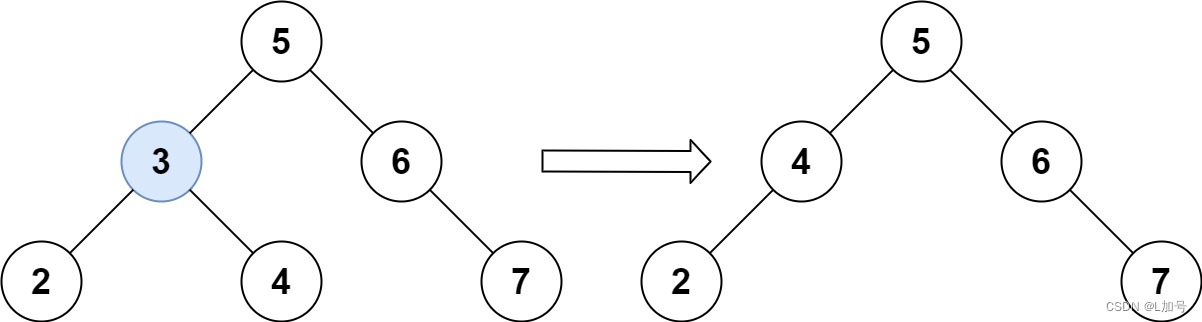
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
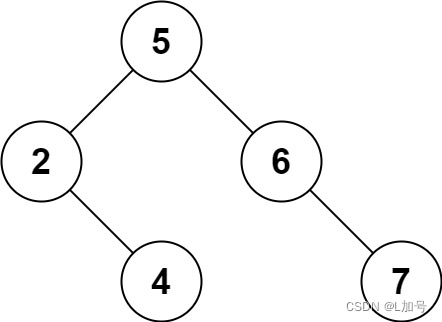
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105
思路
-
参数:节点,删除值
-
返回值:节点
-
终止条件: 找到节点 或 未找到节点
-
单次递归(一条路径)
节点为五种情况
- 未找到节点
- 节点无左右子树
- 节点有左子树,无右子树,则删除节点,左子树补位,返回左子树
- 节点有右子树,无左子树,则删除节点,右子树补位,返回右子树
- 节点左右子树都有,删除节点,右子树补上,将左子树成为右子树的最左边节点的左孩子(将左子树节点成为右子树最小值节点的左孩子)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root==NULL) return root;//未找到节点
if(root->val>key){
root->left=deleteNode(root->left,key);
}
if(root->val<key){
root->right=deleteNode(root->right,key);
}
if(root->val==key){
if(root->left==NULL && root->right==NULL){//节点无左右子树
delete root;
return NULL;
}
else if(root->left==NULL && root->right!=NULL){//节点有左子树,无右子树,
//则删除节点,左子树补位,返回左子树
TreeNode* rightnode=root->right;
delete root;
return rightnode;
}
else if(root->left!=NULL && root->right==NULL){//节点有右子树,无左子树,
//则删除节点,右子树补位,返回右子树
TreeNode* leftnode=root->left;
delete root;
return leftnode;
}
else{//节点左右子树都有,删除节点,右子树补上,
//将左子树成为右子树的最左边节点的左孩子
//(将左子树节点成为右子树最小值节点的左孩子)
TreeNode* cur=root->right;
while(cur->left!=NULL){
cur=cur->left;
}
cur->left=root->left;
TreeNode* node=root->right;
delete root;
return node;
}
}
return root;
}
};