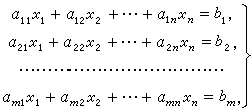目录

前言

1.双关节机械手臂模型

1.1 实际模型

1.2 名义模型

2. 控制律设计

3. 神经网络补偿自适应律设计

3.1自适应律①

3.2自适应律②

4. 仿真分析

4.1仿真模型

4.2 仿真结果

4.3 小结

5学习问题

---

前言

所谓的补偿可以简单的理解为：将扰动的模型估计出来，对这部分已知的扰动数学模型单独设计控制器进行补偿，本章以神经网络自适应补偿对机械手臂模型的不确定进行补偿控制，为外界扰动和未建模扰动归结为总扰动设计自适应律，从而达到模型的跟踪控制。

1.双关节机械手臂模型

1.1 实际模型

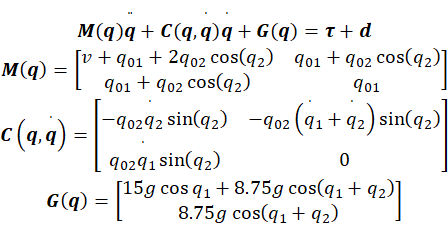
1.2 名义模型

定义名义模型参数为M0(q),C0(q,q')和G0(q)，所以有ΔM=M0-M，ΔC=C0-C和ΔG=G0-G，即：

所以名义机械手臂模型为：

其中：f=ΔM*q''+ΔC*q'+ΔG+d

2. 控制律设计

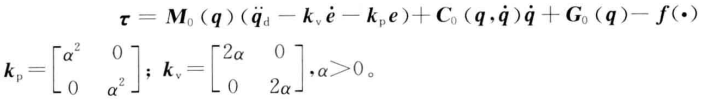
3. 神经网络补偿自适应律设计

对于补偿控制可以理解为对扰动f的逼近，之后在所设计的控制律中以估计值f^呈现

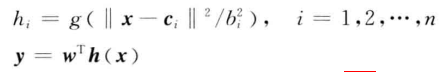
 其中：

①x=[e;de]，如果系统为二阶则x=[e1;e2;de1;de2]，以此类推；

②h为高斯函数的输出，所以c和b即为高斯参数;

③y为神经网络的输出，即逼近扰动f的f^;

④w为神经网络的权值，也是自适应律w'的状态，理论上权值数量越多估计越精确

3.1自适应律①

 其中：

①γ为调节逼近的参数

②P为实对称正定矩阵，其求解方法为：

（1）推导出逼近误差状态空间表达式

 （2）利用满足误差方程的Lyapunov矩阵，通常选取Q为对角矩阵

3.2自适应律②

 其中：k>0，其余与自适应律1同。

4. 仿真分析

4.1仿真模型

名义模型参数：v=15，q01=10，q02=10

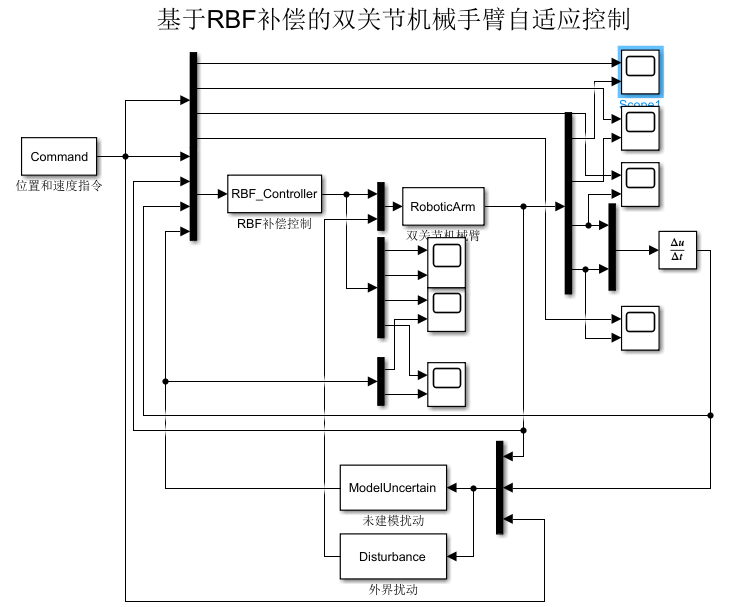
4.2 仿真结果

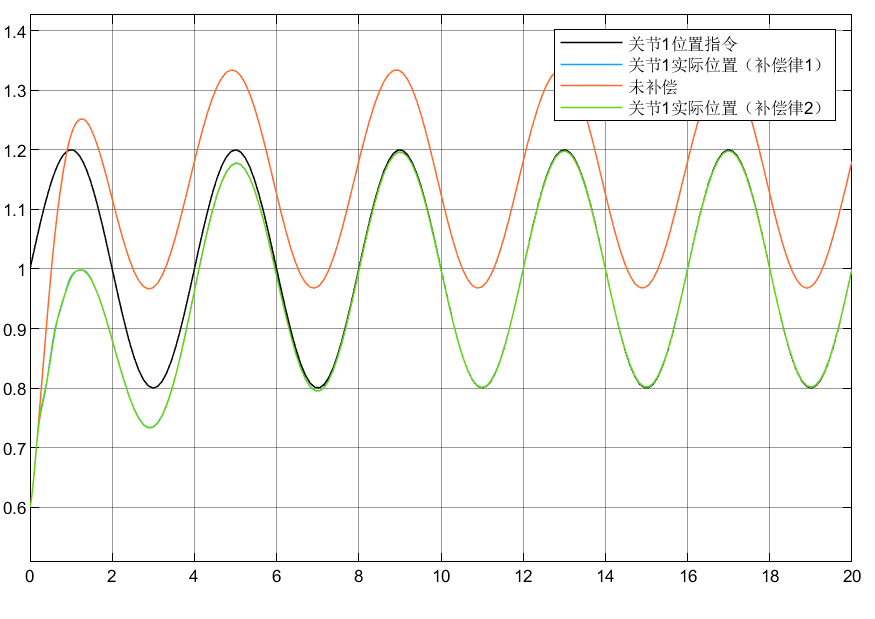
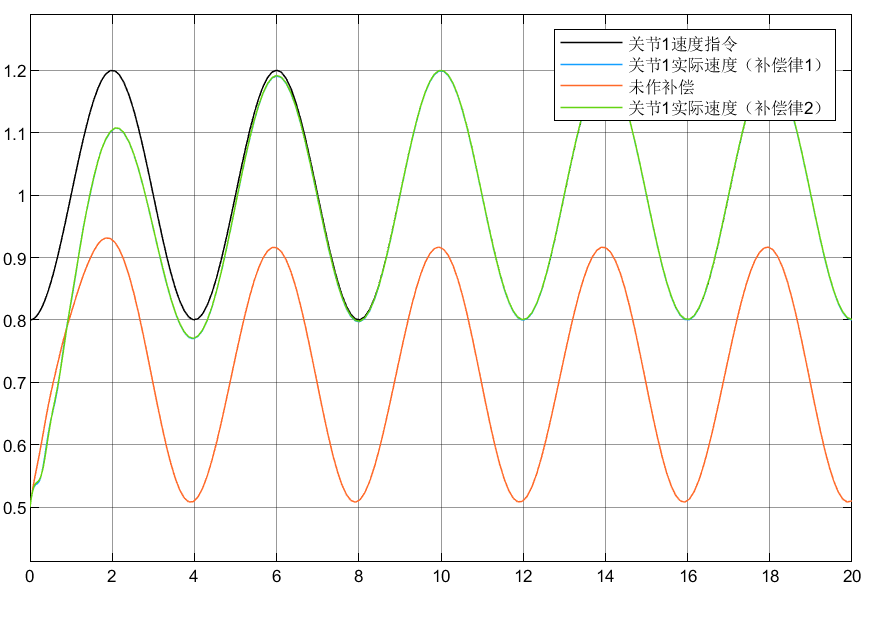
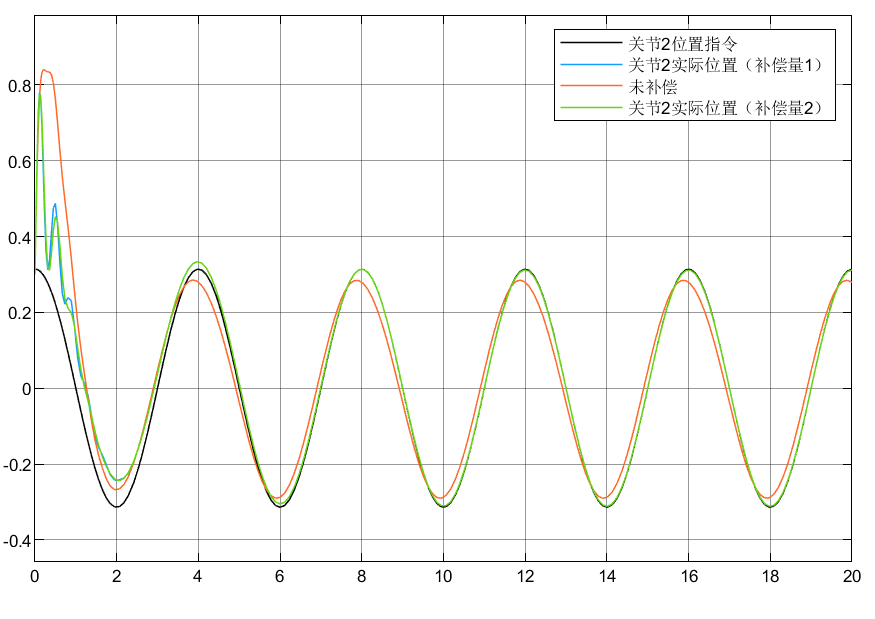
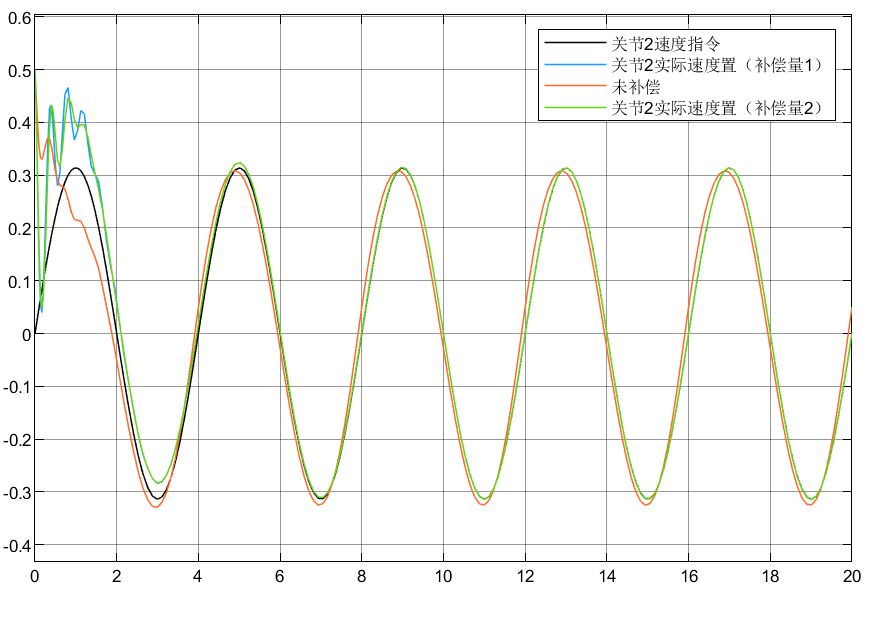
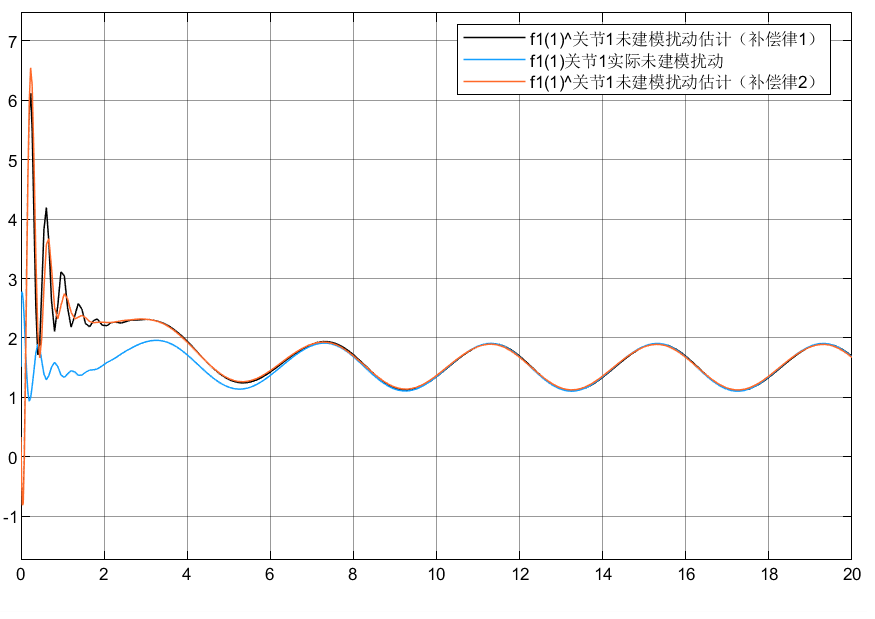
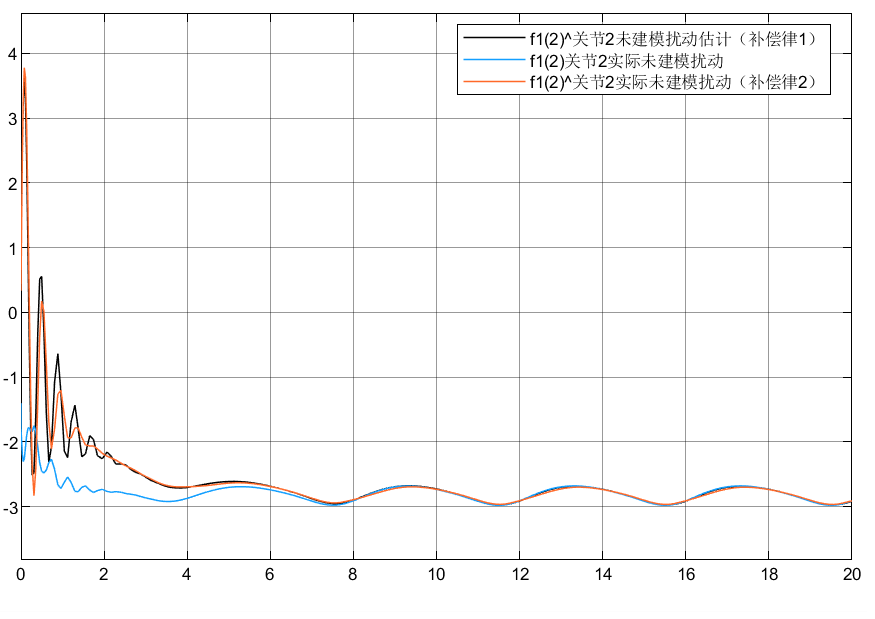
4.3 小结

①可以看到对于含神经网络补偿控制的指令跟踪比未补偿时效果要好

 ②对于两种自适应律比较可以看到，自适应律②相较补偿更好

5学习问题

①对于补偿的量可以是单独的未建模扰动，也可以是单独的外界扰动，或者是两种的扰动总和，但前提都需要已知名义模型和扰动的数学模型，但是在本例中为什么我在更换的时候却发现补偿不佳呢？

②对于逼近误差方程B矩阵的选取，推导后的B矩阵含M的逆，为什么我这里只能将Inv(M0)替换为eye(2)，否则效果不佳？

③对于本例中的f实际上的inv(M0)*f，即f1=inv(M0)*f，但是按推导来应该是直接补偿f，这是为何？有待后续调试考察程序和模型。