假设检验

假设检验的基本原理

提出假设

假设检验：先对总体提出某种假设（例如对总参数提出一个假设值），然后利用样本信息判断这一假设是否成立
原假设：也称零假设，通常是研究者想搜集证据予以推翻的假设，记为$H_0$ ；原假设表达的含义是指参数没有变化、变量之间没有联系或总体分布与一理论分布并无差异，所以常有$=$。设参数的假设值为${\mu }_0$，原假设常写成 $H_0:\mu ={\mu }_0;H_0:\mu \ge {\mu }_0;H_0:\mu \le {\mu }_0$ 。原假设最初被假设是成立的，之后根据样本数据确定是否有足够的证据拒绝原假设。
备则假设：通常是研究者想搜集证据予以支持的假设，记为$H_1$或$H_a$；备则假设表达的含义是指参数有变化、变量之间有联系或总体分布与一理论分布有差异。因此备则假设常写成 $H_1:\mu \ne {\mu }_0;H_1:\mu >{\mu }_0;H_1:\mu <{\mu }_0$。备则假设通常用于表达研究者自己倾向于支持的看法，然后就是想办法收集证据拒绝原假设，支持备则假设。

• 双侧检验：也称双尾检验，指没有特定方向性的备则假设，含有符号$\ne$
• 单侧检验：也称单尾检验，指有特定方向性的备则假设，含有符号$>$（右侧检验）或$<$（左侧检验）
  （备则假设就是我们为什么要检验的理由，例如我们检验一个车间生产的零件是否符合标准，我们肯定是认为它不符合标准才需要检验，要是我们认为它标准的话就没必要检验了。因此原假设是符合标准，备择假设是不符合标准）

作出决策

两类错误：

• 第 I 类错误：也称为 $\alpha$ 错误，原假设是正确的却拒绝了原假设，概率记为 $\alpha$
• 第 II 类错误：也称为 $\beta$ 错误，原假设是错误的却没有拒绝了原假设，概率记为 $\beta$

在样本量一定的情况下，$\alpha$ 与 $\beta$ 是负相关的；要是 $\alpha$ 和 $\beta$ 同时减小只能增大样本量。

显著性水平：即 $\alpha$，通常是人们事先指定的犯第一类错误的概率的最大允许值；一般情况下，人们认为第一类错误的后果更严重，因此会取一个较小的 $\alpha$ 值，实际中常用 $\alpha =0.01$ ，$\alpha =0.05$ 和 $\alpha =0.1$

① 用统计量决策：首先要根据样本观测结果计算对原假设作出决策的检验统计量。例如要检验总体均值，则可以对样本均值标准化（标准化检验统计量）；然后根据实现确定好的显著性水平 $\alpha$ 划定拒绝域：
$$标准化检验统计量=\frac{点估计-假设值}{点估计量的标准差}$$

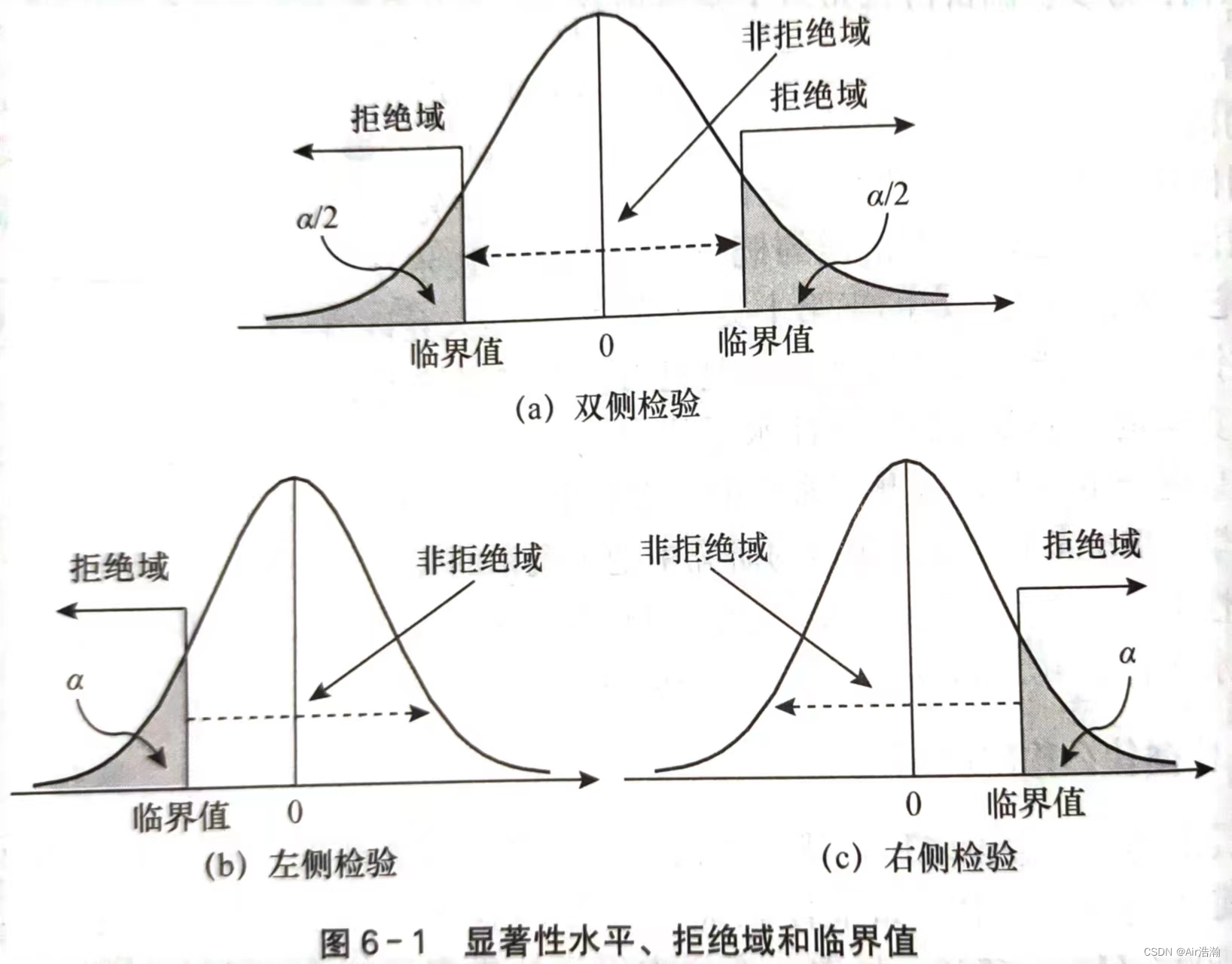
决策准则：

• 双侧检验：|统计量|>临界值，拒绝原假设
• 左侧检验：统计量的值<-临界值，拒绝原假设
• 右侧检验：统计量的值>临界值，拒绝原假设

② 用 $P$ 值决策：如果原假设是正确的，所得到的样本结果会像实际观测结果那么极端或者更极端的概率称为 $P$ 值 ，也称观察到的显著性水平。

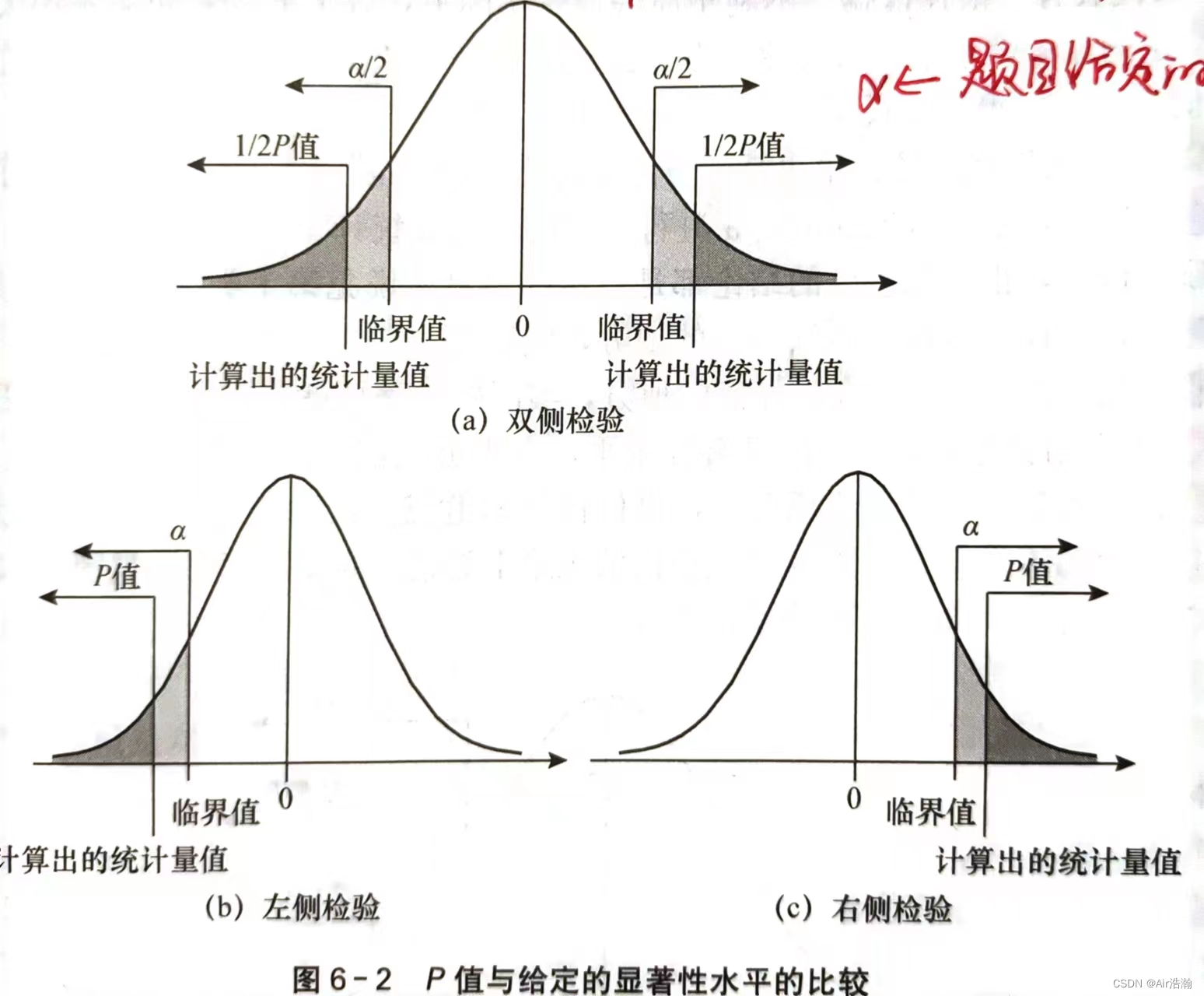
决策准则：

• 如果 $P<\alpha$ ，则拒绝 $H_0$
• 如果 $P>\alpha$ ，则不拒绝 $H_0$

注意：

• $P$ 值是关于数据的概率，与原假设对错的概率无关；$P$ 值反映的是某个总体的所有样本中某一类数据出现的经常程度。就是说当原假设是正确时，$P$ 值就是得到目前这个样本的概率。

（书上解释的跟屎一样；比如我们要检验全小学生月平均生活支出是否为 $2000$ 元，$H_0:\mu =2000$ ，我们统计出来 $\bar{X}=1750$ ，$P=0.02$，$\alpha =0.05$ ，说明如果平均支出真的是 $2000$ 的话，那么我们抽到 $1750$ 的概率只有 $0.02$，太小了，所以可以拒绝原假设）

• $P$ 值不一定要和显著性水平 $\alpha$ 进行比较，我们可以认为 $P$ 值越小，拒绝原假设的理由就越充分，一般要求 $P$ 不大于 $0.1$
• $P$ 值决策优于统计量决策，$P$ 值其实是实际上犯 I 类错误的概率。

表述决策结果

• 假设检验不能证明原假设正确，“不拒绝”不代表“接受”，接受 $H_0$ 的风险由 $\beta$ 衡量；
• 拒绝原假设时，称样本结果在“统计上是显著的”，“显著的”意思是“非偶然的”，但统计上显著不等于有实际意义

一个总体参数的检验

总体均值的检验

大样本的检验：样本均值经标准化后，可认为服从标准正态分布，因而采用正态分布的检验统计量：

• 当总体方差 ${\sigma }^2$ 已知时，总体均值检验统计量为：

$$Z=\frac{\bar{X}-{\mu }_0}{\sigma /\sqrt{n}}$$

• 当总体方差 ${\sigma }^2$ 未知时，可以用样本方差 $S^2$ 代替，得到总体均值检验统计量为：

$$Z=\frac{\bar{X}-{\mu }_0}{S/\sqrt{n}}$$

小样本的检验：

• 当总体方差 ${\sigma }^2$ 已知时，即使是在小样本的情况下，样本均值经标准化后仍然服从标准正态分布，总体均值检验统计量为：

$$Z=\frac{\bar{X}-{\mu }_0}{\sigma /\sqrt{n}}$$

• 当总体方差未知时，检验统计量满足 t 分布（自由度为 $n-1$ ），通常称为 t 检验

$$t=\frac{\bar{X}-{\mu }_0}{S/\sqrt{n}}$$

总体比例的检验

大样本的检验：样本比例经过标准化后近似服从标准正态分布，因此总体比例检验统计量为：（${\pi }_0$ 可以是我们猜测的比例）
$$Z=\frac{p-{\pi }_0}{\sqrt{\frac{{\pi }_0(1-{\pi }_0)}{n}}}$$

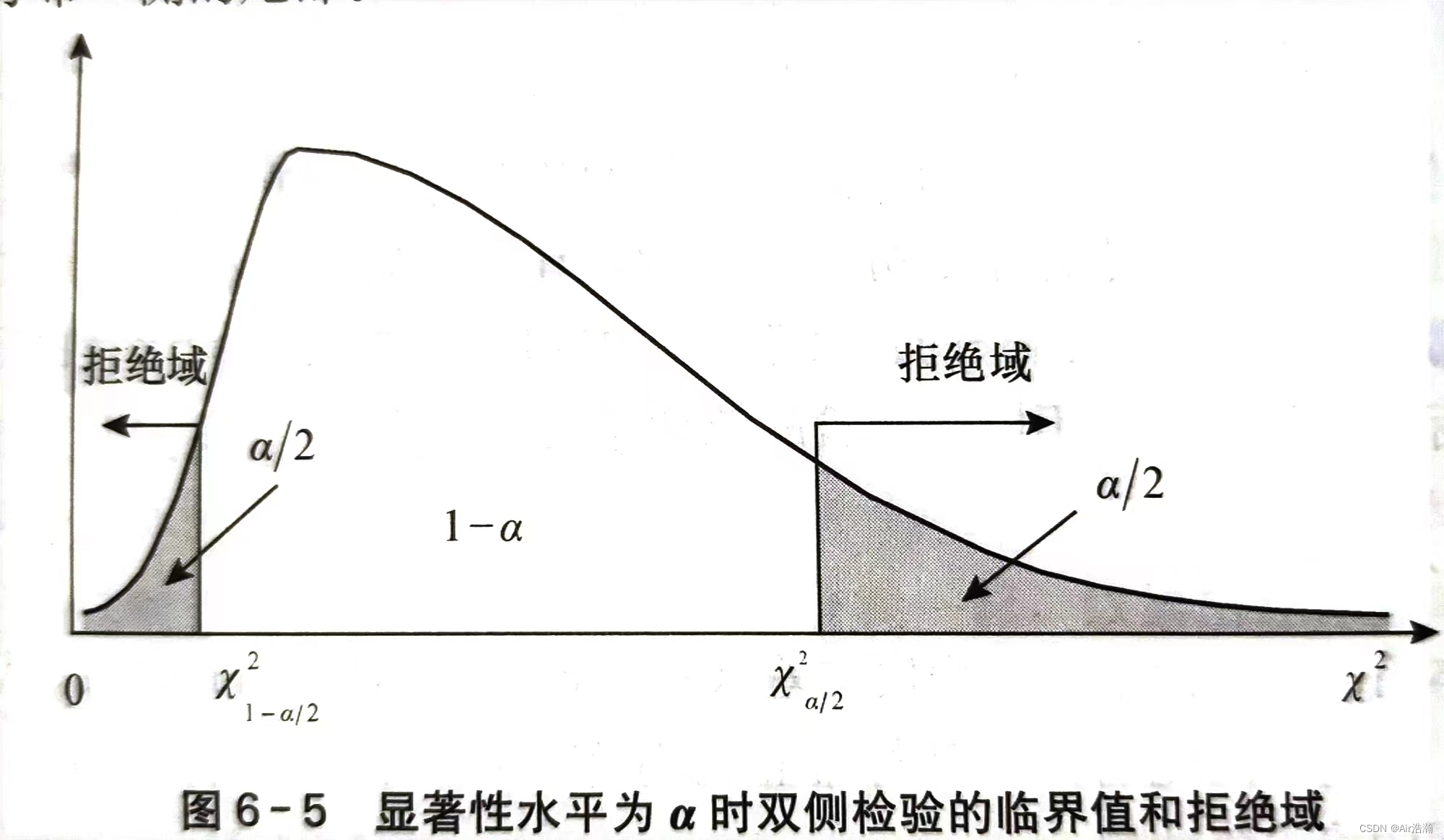
总体方差的检验

总体方差的检验，不论样本量 $n$ 是大是小，都要求总体服从正态分布。总体方差检验统计量为：（${\sigma }_0$ 可以是我们猜测的方差）
$${\chi }^2=\frac{(n-1)S^2}{{\sigma }_0^2}$$
（${\chi }^2$ 自由度为 $n-1$ ）由于是不对称分布，因此我们采取等尾区间：

两个总体参数的检验

两个总体均值之差的检验

（常用于比如比较两个相似环境下产生的结果是否相同，取 $H_0:({\mu }_1-{\mu }_2)=0$ ）

独立大样本的检验：两样本均值之差经标准化后满足正态分布（$({\mu }_1-{\mu }_2)$ 为我们猜测的样本均值之差的值）

• 当总体方差 ${\sigma }_1^2$ 和 ${\sigma }_2^2$ 已知时，总体均值检验统计量为：

$$Z=\frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}$$

• 当总体方差 ${\sigma }_1^2$ 和 ${\sigma }_2^2$ 已知时，分别使用样本方差 $S_1^2$ 和 $S_2^2$ 代替，总体均值检验统计量为：

$$Z=\frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$

独立小样本的检验：

• 当总体方差 ${\sigma }_1^2$ 和 ${\sigma }_2^2$ 已知时，样本均值之差经标准化后仍然服从标准正态分布，总体均值之差检验统计量为：

$$Z=\frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}$$

• 当总体方差 ${\sigma }_1^2$ 和 ${\sigma }_2^2$ 未知，但 ${\sigma }_2^2={\sigma }_2^2$ 时，需要将两个样本数据组合在一起，组合后的样本方差 $S_p$ 为：

$$S_p=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}$$

样本均值之差标准化后符合自由度为 $n_1+n_2-2$ 的 t 分布，检验统计量为：
$$t=\frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$

• 当总体方差 ${\sigma }_1^2$ 和 ${\sigma }_2^2$ 未知且 ${\sigma }_2^2\ne {\sigma }_2^2$ 时，样本均值之差标准化后近似服从自由度为 $v$ 的 t 分布，检验统计量为：

$$t=\frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$

其中 $v$ 为：（需要四舍五入求整数）
$$v=\frac{(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}{)}^2}{\frac{(\frac{S_1^2}{n_1}{)}^2}{n_1-1}+\frac{(\frac{S_2^2}{n_2}{)}^2}{n_2-1}}$$
配对样本的检验：配对样本的检验需要假定两个总体配对差值构成的总体服从正态分布，且配对差是从差值总体中随机抽取的。对于小样本情形，配对差值经标准化后服从自由度为 $n-1$ 的 t 分布，因此选择的检验统计量为：
$$t=\frac{\bar{d}-({\mu }_1-{\mu }_2)}{S_d/\sqrt{n}}$$
其中 $\bar{d}$ 为配对差值的平均数，$S_d$ 为配对差值的标准差

两个总体比例之差的检验

独立大样本：要求两个样本都是大样本，即 $n_1{p}_1$ ，$n_1(1-p_1)$ ，$n_2{p}_2$ 和 $n_2(1-p_2)$ 都大于等于 $10$ 。根据两个样本比例之差的标准化的抽样分布，可以得到总体比例之差检验统计量为：
$$Z=\frac{(p_1-p_2)-({\pi }_1-{\pi }_2)}{{\sigma }_{p_1-p_2}}$$
其中 ${\sigma }_{p_1-p_2}=\sqrt{\frac{{\pi }_1(1-{\pi }_1)}{n_1}+\frac{{\pi }_2(1-{\pi }_2)}{n_2}}$ 是两个样本比例之差抽样分布的标准差。但是你发现 ${\pi }_1$ 和 ${\pi }_2$ 事先都是不知道的，分为两种情况：

• 检验两个总体比例是否相等，即 $H_0:{\pi }_1-{\pi }_2=0$ ，$H_1:{\pi }_2-{\pi }_2\ne 0$ ；此时 ${\pi }_1$ 和 ${\pi }_2$ 的最佳估计是将两个样本合并后得到的比例，为：

$$p=\frac{p_1{n}_1+p_2{n}_2}{n_1+n_2}$$

此时 ${\sigma }_{{\pi }_1-{\pi }_2}$ 的最佳估计量为：
$${\sigma }_{{\pi }_1-{\pi }_2}=\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}$$
代入得到两个总体比例之差的检验统计量为：
$$Z=\frac{p_1-p_2}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}}$$

• 检验两个总体比例之差是否是个常数，即 $H_0:{\pi }_1-{\pi }_2=d_0$ ，$H_1:{\pi }_2-{\pi }_2\ne d_0$ ，这时可直接用两个样本的比例 $p_1$ 和 $p_2$ 作为两个总体比例 ${\pi }_1$ 和 ${\pi }_2$ 的估计，从而得到两个总体比例之差的检验统计量为：

$$Z=\frac{(p_1-p_2)-d_0}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}$$

（也有可能是这样：$H_0:{\pi }_1-{\pi }_2\ge 0$ ，$H_1:{\pi }_1-{\pi }_2<0$ 或者 $H_0:{\pi }_1-{\pi }_2\le 0$ ，$H_1:{\pi }_1-{\pi }_2>0$ ，都当作第一种来处理，要注意等号总是在原假设里）

两个总体方差比的检验

对总体方差比的假设通常是跟 $1$ 相比，就是看两个总体谁的方差更大一些。由于两个样本方差之比 $\frac{S_1^2}{S_2^2}$ 是两个总体方差之比 $\frac{{\sigma }_1^2}{{\sigma }_2^2}$ 的理想估计量，故检验统计量为：（符合 $F(n_1,n_2)$ 分布）
$$F=\frac{S_1^2}{S_2^2}$$
双侧检验通常是用较大的样本方差除以较小的样本方差，这样拒绝域总是发生在 F 分布的右侧。在左侧检验时，也可以安排为右侧检验。

总体分布的检验

总体正态性检验：根据样本数据检验总体上是否服从正态分布，检验方法有图示法和检验法。

正态性检验的图示法

正态概率图：有两种：

• $Q-Q$ 图：根据观测值的实际分位数与理论分布（如正态分布）的分位数绘制的
• $P-P$ 图：根据观测数据的累积概率与理论分布（如正态分布）的符合程度绘制的

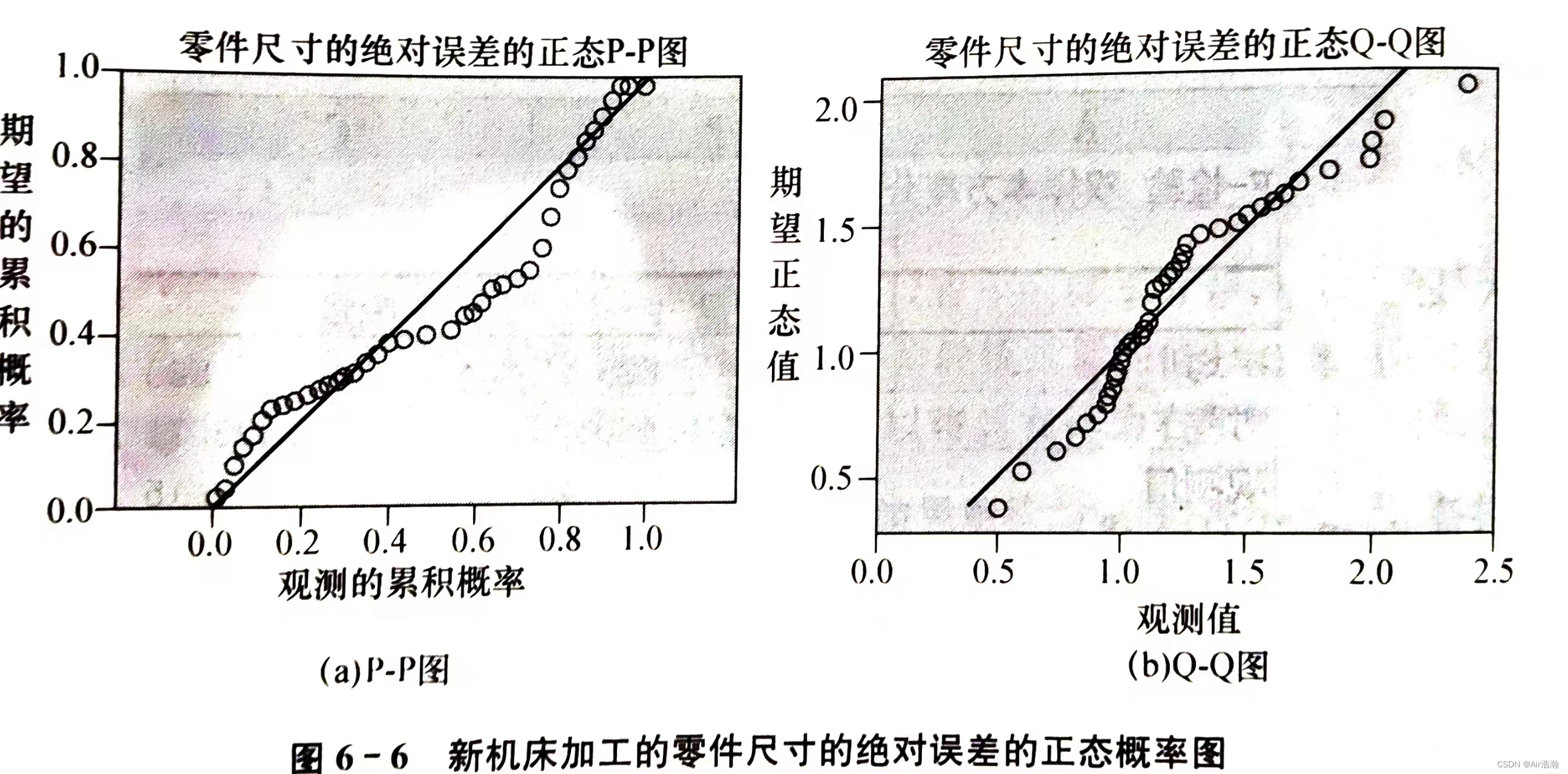
• 图中直线表示理论正态分布线，各观测点越靠近直线，且呈随机分布，表明数据越接近正态分布。

• 实际使用时并不一定要参考理论正态分布线，只要所有点都在一条直线的周围随机分布即可

• 由于正态概率图中的点很少，提供的正态性信息有限，适用于大样本量；

Shapiro-Wilk 和 K-S 正态性检验

当样本量较小时，可以使用标准的统计检验办法，即假设总体服从正态分布，如果检验获得的 $P$ 值小于显著性水平 $\alpha$ ，则拒绝原假设。

Shapiro-Wilk 方法：（适用于小样本）$H_0$ ：总体服从正态分布，$H_1$ ：总体不服从正态分布，然后计算检验统计量 $W$ ：
$$W=\frac{\sum a_i{y}_i^2}{\sum (y_i-\bar{y}{)}^2}$$

• $y_i$ 为排序后的样本数据，$\bar{y}$ 是样本均值
• $a_i$ 时样本量为 $n$ 所对应的系数，通过：

$$\left[\begin{array}{c}{a}_1,\cdots ,a_n\end{array}\right]=\frac{m^T{V}^{-1}}{||V^{-1}m||}$$

• $V$ 是这些有序统计量的协方差
• $m=\left[\begin{array}{c}{m}_1,\cdots ,m_n\end{array}\right]$ ，其中 $m_i$ 是从一个标准的正态分布随机变量上采样的有序独立同分布的统计量的期望值

$W$ 的最大值是 $1$ ，最小值是 $\frac{n{a}_1^2}{n=1}$ ，统计量越大表示越符合正态分布。当然，非正态分布的小样本数据也有可能有较大的 $W$ 值，而且由于该统计量的分布是未知的，因此需要通过模拟或者查表来估计概率。

Kolmogorov-Smirnov 检验：既适合大样本，又适合小样本，而且不止可以检验正态分布。将实际频数和期望频数进行比较，检验其拟合程度。具体来说，是将某一变量的积累分布函数与特定的分布函数进行比较。设总体的积累分布函数为 $F(x)$ ，已知理论分布函数为 $F_0(x)$ ，则：
$$H_0:F(x)=F_0(x);H_1:F(x)\ne F_0(x);$$
各样本观察值的实际累计概率为 $S(x)$ ，实际累计概率与理论累计概率的差值为 $D(x)$ ，差值序列中最大的绝对差值：
$$D=max(|S(x_i)-F(x_i)|)$$
实际累计概率肯定是离散值，因此可以修正为：
$$D=max((|S(x_i)-F(x_i)|),(|S(x_{i-1})-F(x_i)|))$$
在小样本情况下，统计量 $D$ 服从 Kolmogorov 分布；在大样本情况下，则用正态分布近似，统计量为：
$$Z=\sqrt{n}D$$
如果原假设成立，则每次抽样得到的 $D$ 值应当不会偏离 $0$ 太远。

K-S要求样本数据是连续的数值型数据，且要求理论分布已知。总体均值和方差未知时也可以用 $\bar{X}$ 和 $S^2$ 代替。

总结