机器学习100天,今天讲的是:KD树的构造和搜索!
《机器学习100天》完整目录:目录
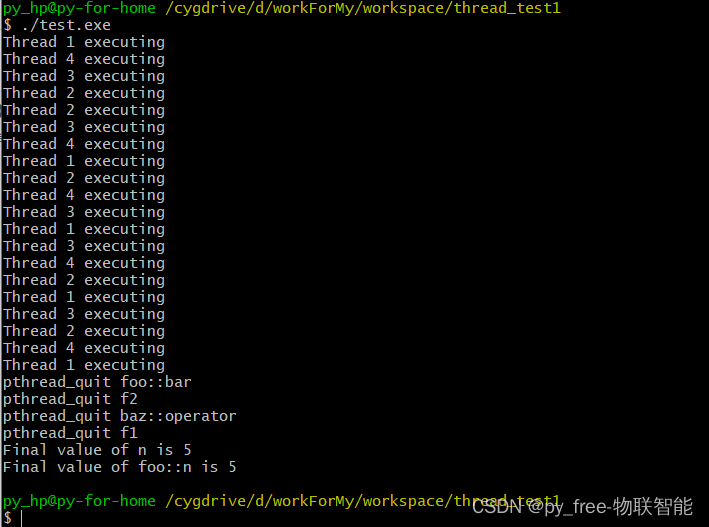
在 K 近邻算法中,我们计算测试样本与所有训练样本的距离,类似于穷举法。如果数据量少的时候,算法运行时间没有大的影响,但是如果数据量很大,那么算法运行的时间就会很长。这在实际的应用中效率很低。
因此,为了最快地进行检索,就提出了一种新的算法:KD树(k-dimensional tree)。KD树是二叉树的一种,是对 k 维空间的一种分割,不断地用垂直于坐标轴的超平面将k维空间切分,形成 k 维超矩形区域。KD 树可以帮助我们在很快地找到与测试点最邻近的 K 个训练点。不再需要计算测试点和训练集中的每一个数据的距离。下面我将以最通俗的语言来介绍。
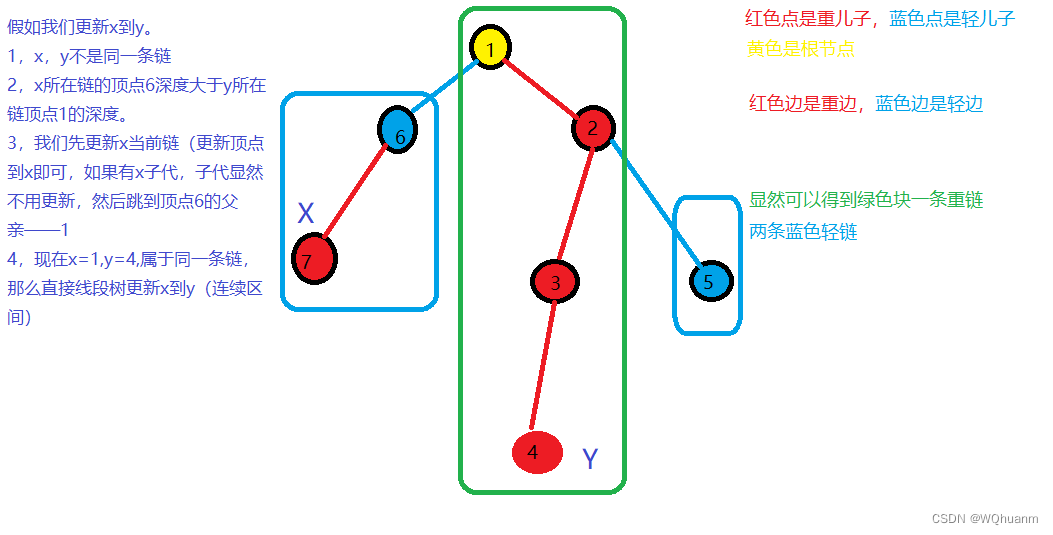
要完全掌握 KD 树,只要记住两个步骤:一是 KD 树的构造,二是 KD 树的搜索。
一、KD 树的构造
首先我们来看 KD 树的构造,举个例子。二维平面上有 13 个点,分布如图所示。
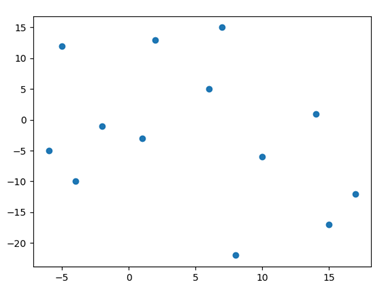
该 13 个点的坐标为:([6,5], [1,-3], [-6,-5], [-4,-10], [-2,-1], [-5,12], [2,13], [17,-12], [8,-22], [15,-17], [10,-6], [7,15], [14,1])。
首先,第一步,选取一个维度,