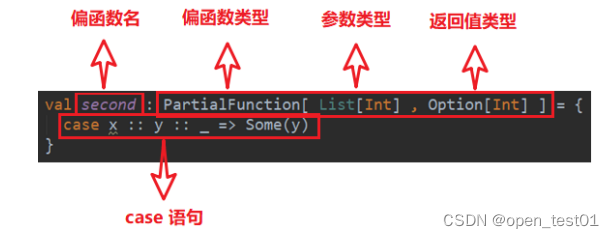
11-12第一学期A

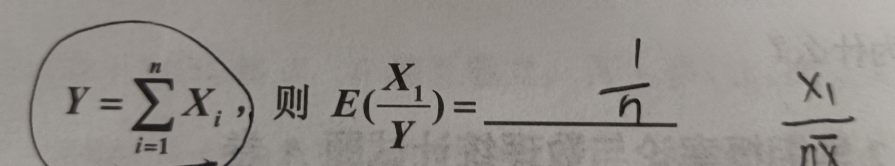
1 略。
2 X服从正态分布N(0,1),X^2服从卡方分布。又考查了卡方分布均值和方差公式。一开始如果对本题无从下手,大概是没看出来是什么分布。
3 第二小空本身也可以作为一个结论。
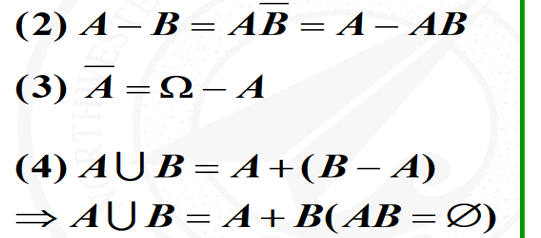
4 考查切比雪夫不等式,不会中规中矩给出EX、DX让你带入就行了。比如本题,告诉你X、Y相互独立就是引导你去构造。
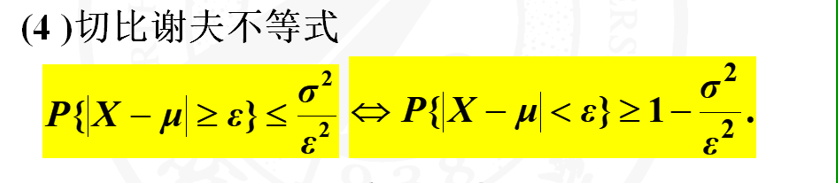
5 指数分布方差、期望分别为λ^-1、λ^-2。注意是以λ为参数时,有的题会以λ倒数为参数。
6 略。这种一时感觉糊涂,也可以直接把所有情况列出来。
7 给出p(x)没有用上的确有些疑惑。
11-12第二学期A

1 本题关键点在于明确BA和BA杠关系。
2 泊松分布。均值和方差均为λ。EX^2=(E(X))^2+D(X),先求出λ为2,再利用泊松分布公式即可。而且本题也考查了泊松分布k取值从0开始的整数。
3 得先求F(X)。
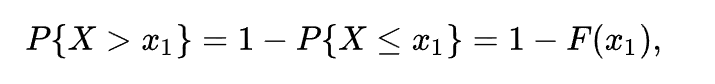
容易求出每次X大于1可能性为5/8,这时候它引入了一个Y,很明显就是个二项分布。方差np(1-p),得出15/8.
这种题之所以难受,让人有时候绕里面去了,耽误时间,主要就是它一个分布套着一个分布,你得把每个过程捋清楚。
4 熟练写出指数分布分布函数,计算结果来个五次方(积事件)。
5 切比雪夫不等式内外两个号是反的。
6 正态分布对称性,简单的题分不能丢。
7 直白考查二项分布期望np 方差np(1-p)
8 填空题里考的矩估计一般较为简单,掌握原始基本分布的期望公式一般即可。
9 跟6同考点。
12-13第一学期A

1 略。
3 当时我做这个题的时候,没复习到t分布,这个直接寄了。
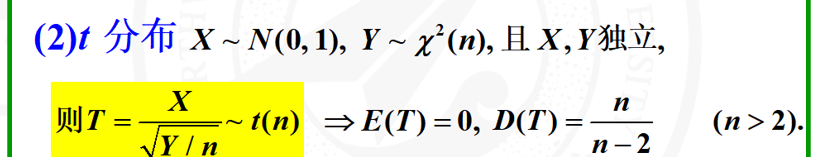
值得注意的是1/T^2为F分布,可视为结论。
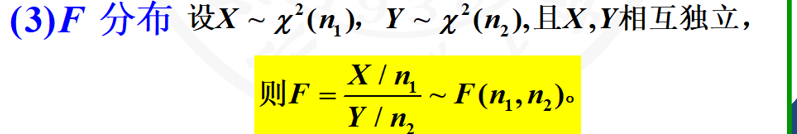
4 协方差和相关系数考查。值得注意的是上学期那个卷子也考了。
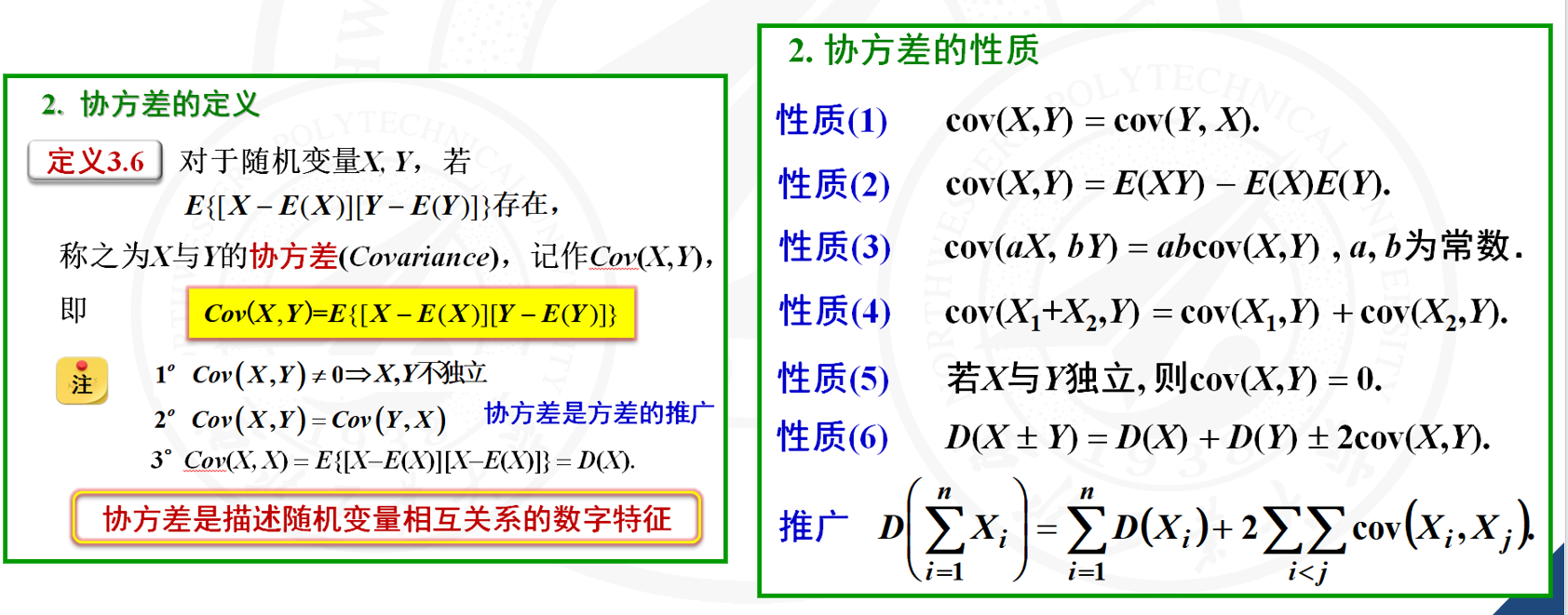
5 这就有点离谱了哈。双正态总体参数显著性水平检验,这种F分布构造出大题都有点那个,你出填空...