本讲目标
●理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。
●学握Eigen库的矩阵、几何模块使用方法。
旋转矩阵、变换矩阵

向量外积
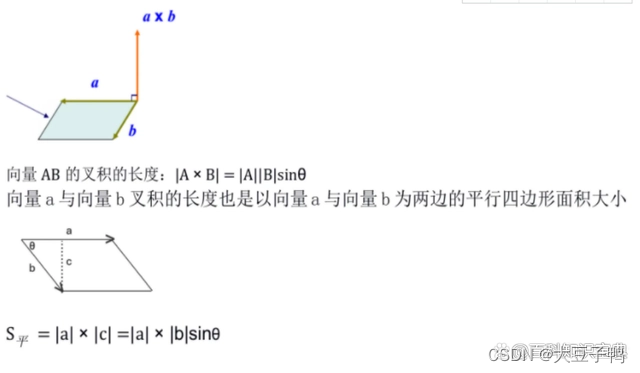
向量外积(又称叉积或向量积)是一种重要的向量运算,它表示两个向量所形成的平行四边形的面积。在几何学中,向量外积的大小是表示两个向量所形成的平行四边形的面积。
a x b 几何意义:a转到b右手坐标系的方向
a x b 大小:就是两个向量所围成的平行四边形的面积。

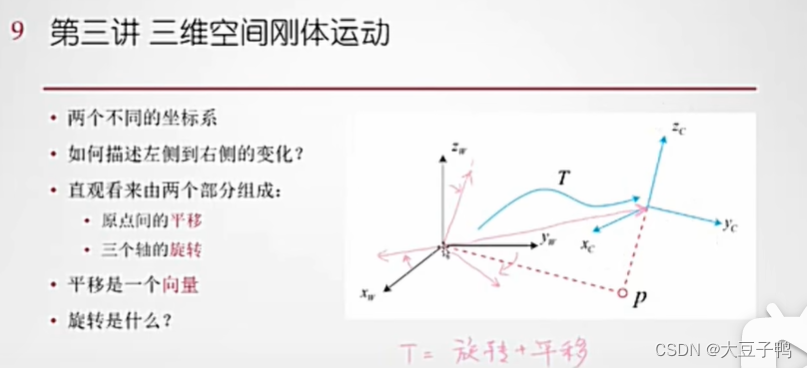
xw世界坐标,xc表示camera相机坐标



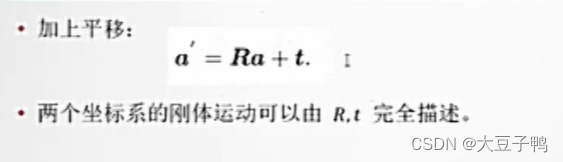


好处:将旋转和平移的动作放在一个矩阵中,这样每次变换就可以先进行旋转和平移动作的全部叠加,变换矩阵。

TWR 表示机器人坐标在世界坐标下的位姿,TRW表示世界坐标在机器人坐标下的位姿。
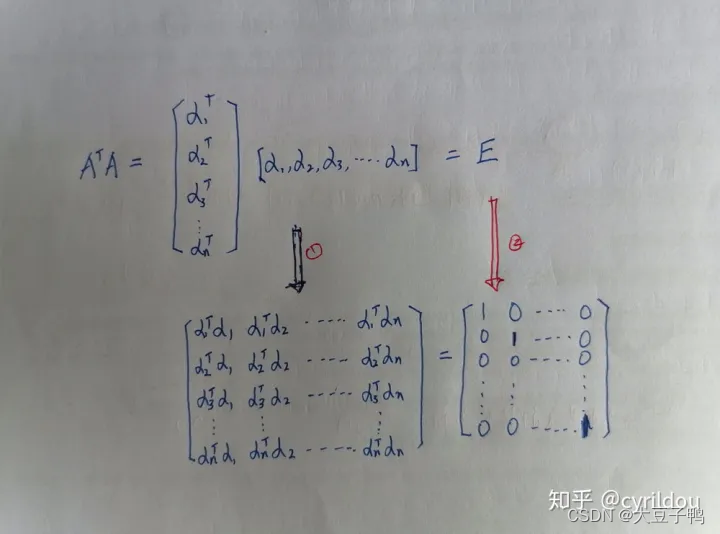
正交矩阵
正交矩阵是指其转置等于逆的矩阵,性质是逆也是正交阵、积也是正交阵。

正交:可以简单理解成就是垂直.
我们假设A是一个列向量矩阵,标识为 A=[ α1,α2,α3·····αn] ,那么按照定义就是:
旋转向量和欧拉角


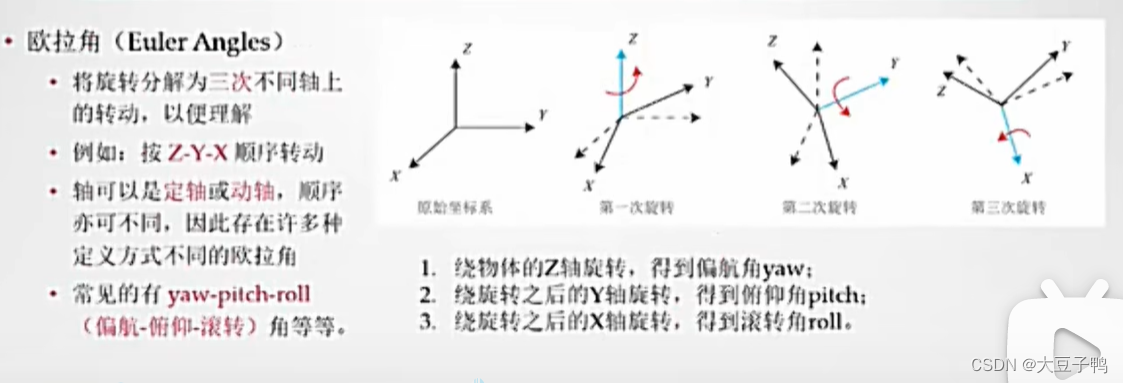
欧拉角:在三维空间中通过指定与三个旋转轴相关联的三个角度来最小参数化表示任意方向。
一共有3种欧拉角:俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)
根据不同的旋转顺序,可以得到很多种欧拉角。
万向锁
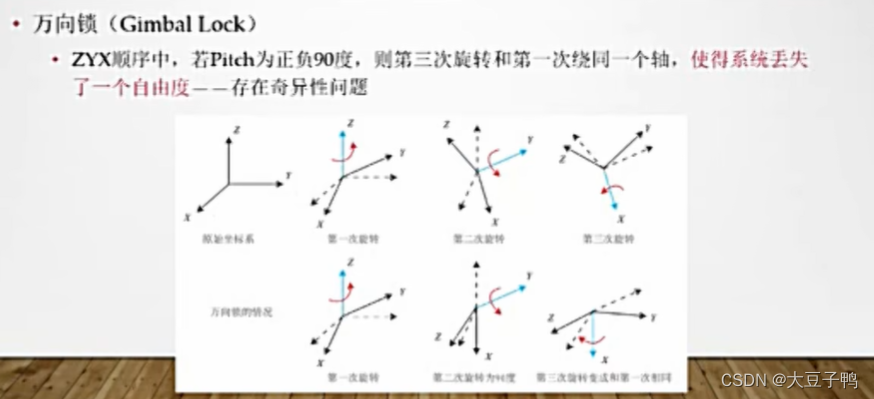

四元数


四元数可以看成扩展的复数,有固定的运算。
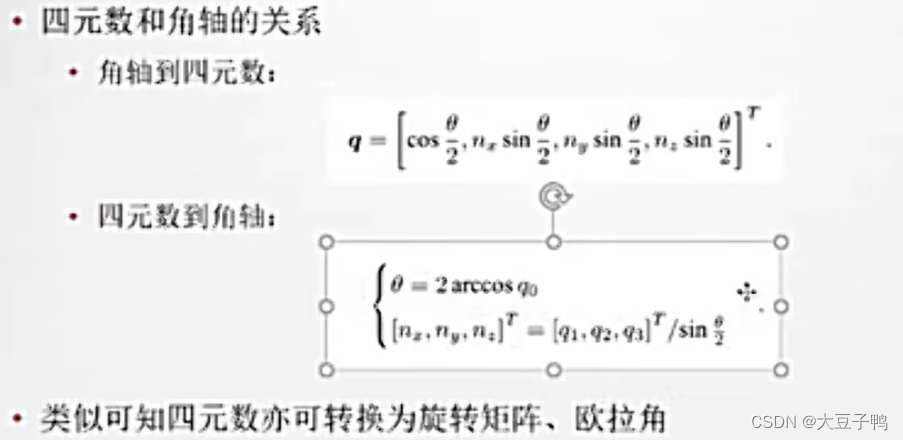

任意一个旋转都可以那一个四元数表示出来,不像欧拉角会受到限制。
参考链接:
向量外积的几何意义是什么
正交矩阵定义和性质
正交矩阵