目录
- 神经网络
- 激活函数
- 引入激活函数原因:
- sigmoid激活函数
- tanh 激活函数
- ReLU 激活函数(最常用)
- SoftMax
- 如何选择
- 反向传播
- 参数初始化方法
- 优化方法
- 正则化
- 批量归一层
- 网络模型调优的思路
神经网络
简单的神经网络包括三层:输入层,隐藏层,输出层。
其中隐藏层可以有很多层,每一层也可以包含数量众多的的神经元。
激活函数
引入激活函数原因:
激活函数用于对每层的输出数据进行变换, 进而为整个网络结构结构注入了非线性因素。此时, 神经网络就可以拟合各种曲线。如果不使用激活函数,整个网络虽然看起来复杂,其本质还相当于一种线性模型。
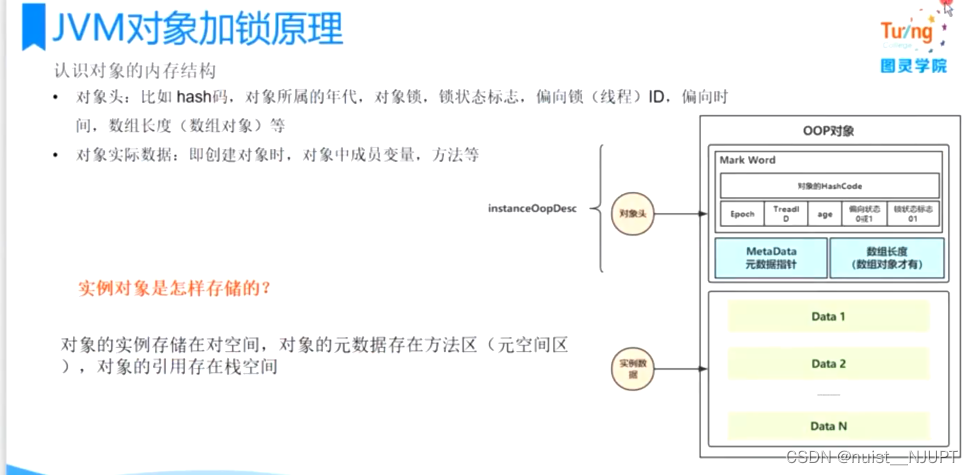
sigmoid激活函数
劣势:
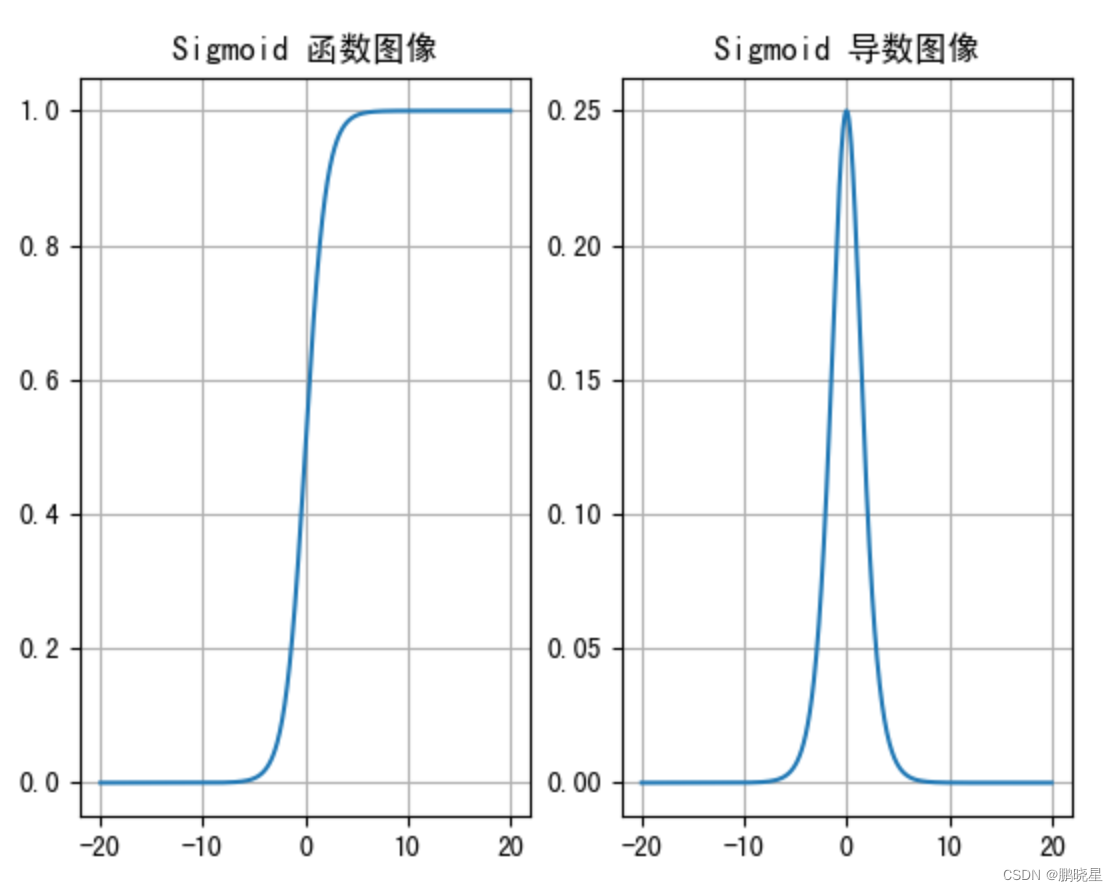
1.当输入 <-6 或者 >6 时,sigmoid 激活函数图像的导数接近为 0,此时网络参数将更新极其缓慢,或者无法更新。
2.一般来说, sigmoid 网络在 5 层之内就会产生梯度消失现象。
3.该激活函数并不是以 0 为中心的,所以在实践中这种激活函数使用的很少。
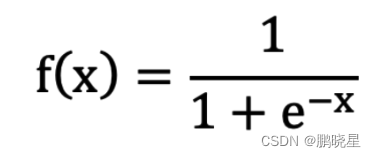
一般用于二分类输出层
tanh 激活函数
优:与 Sigmoid 相比,它是以 0 为中心的,使得其收敛速度要比 Sigmoid 快,减少迭代次数
劣:,当输入的值大概 <-3 或者 > 3 时,其导数近似 0。
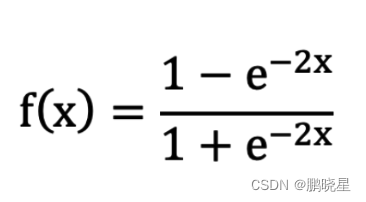
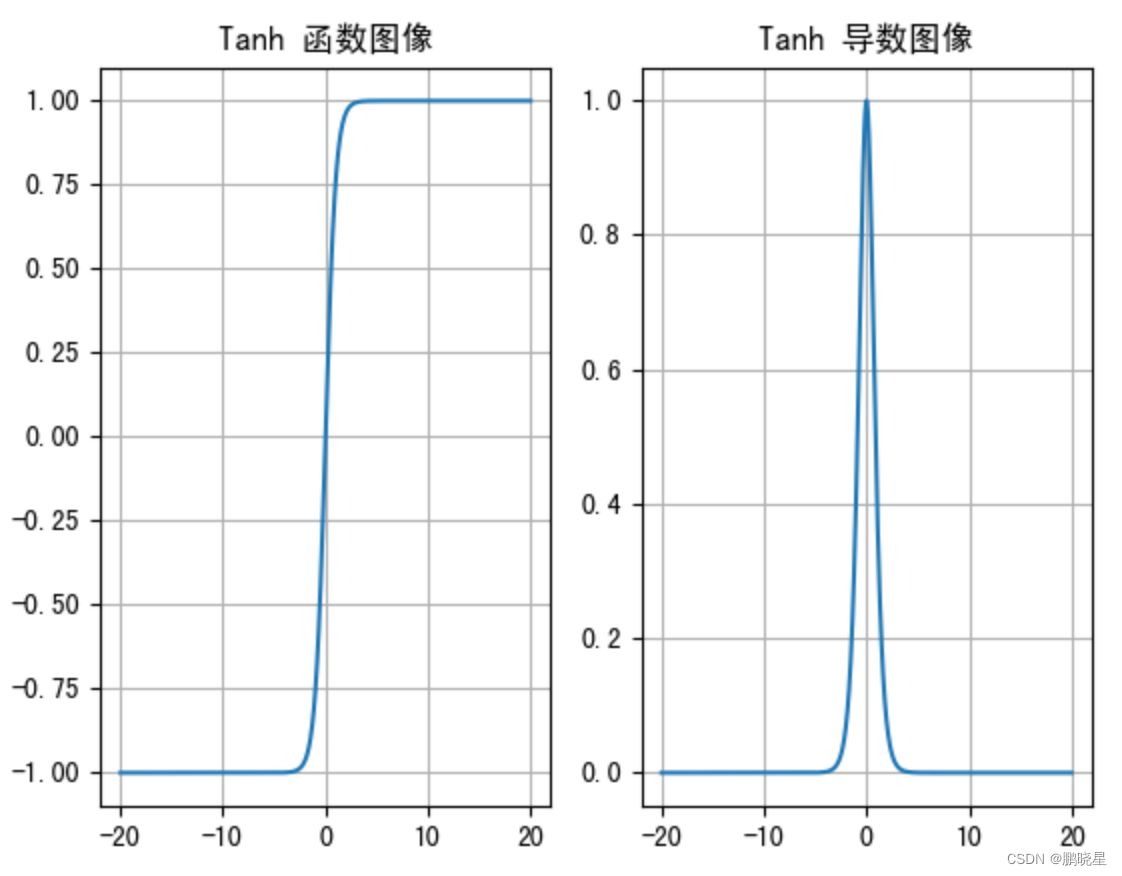
一般用于隐藏层
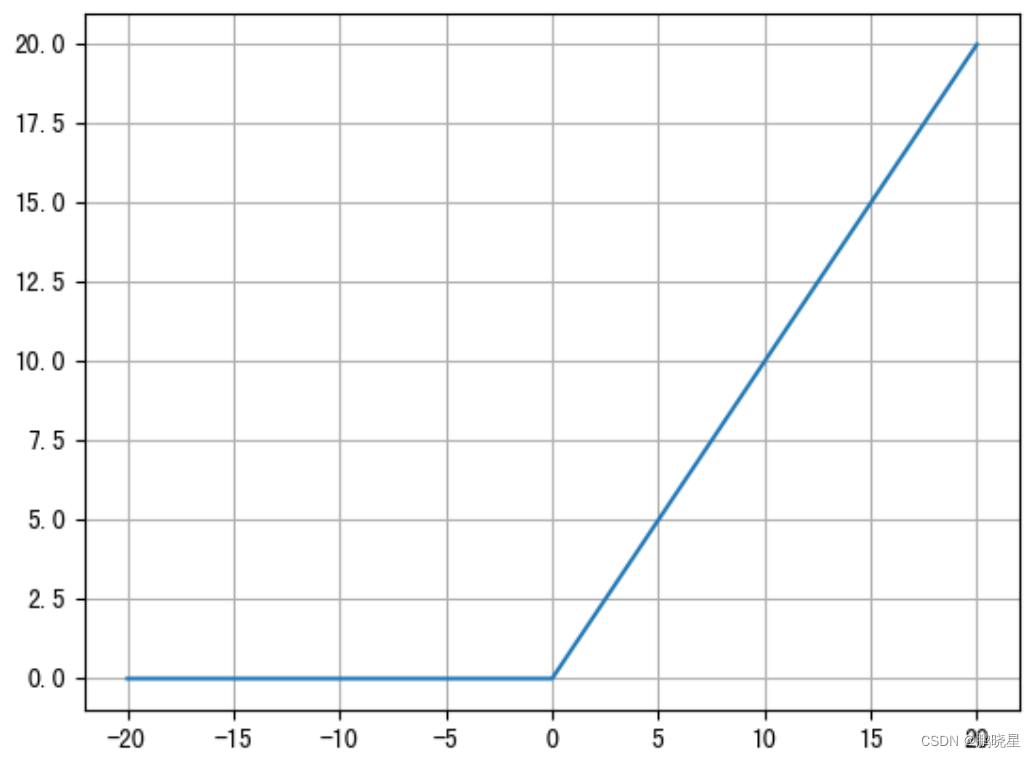
ReLU 激活函数(最常用)
优:
计算量较sigmoid小
Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
公式:f(x) = max(0, x)
函数图像
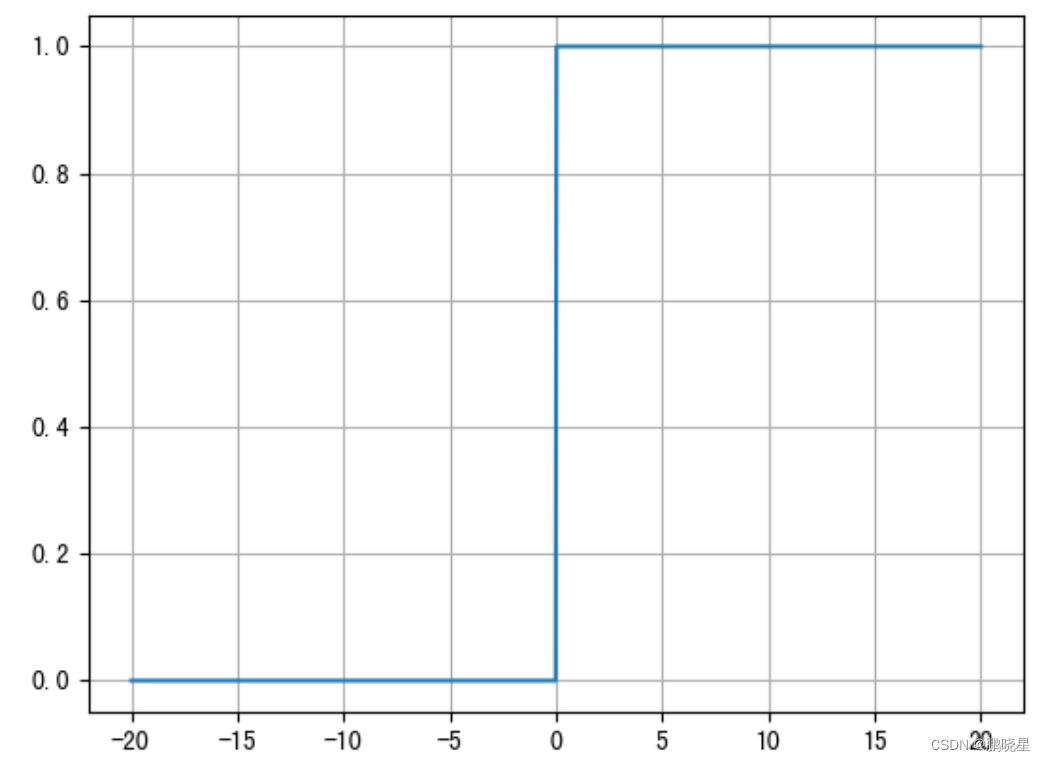
导数图像
SoftMax
用于多分类,以概率形式展现出来
如何选择
隐藏层:优先RELU 不使用sigmoid,可以尝试tanh
输出层:二分类sigmoid, 多分类softmax ,回归identity
反向传播
算法通过链式求导的方法来计算神经网络中的各个权重参数的梯度,从而使用梯度下降算法来更新网络参数。
参数初始化方法
全0
全1
固定值
正态分布
kaiming 初始化,也叫做 HE 初始化. HE 初始化分为正态分布的 HE 初始化、均匀分布的 HE 初始化.
xavier 初始化,也叫做Glorot初始化。两种:正态分布的 xavier 初始化、均匀分布 的xavier 初始化
优化方法
- Momentum
- AdaGrad
- RMSProp
- Adam
正则化
Dropout 层的使用,减一部分梯度归0,达到无法更新参数的目的,用于控制网络复杂度,以此达到正则化的目的
批量归一层
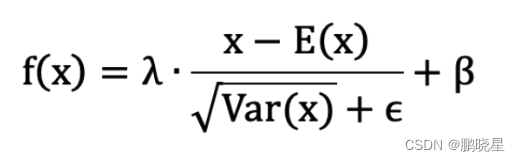
数据在经过 BN 层之后,无论数据以前的分布是什么,都会被归一化成均值为 β,标准差为λ 的分布
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)affine = False 表示 γ=1,β=0,反之,则表示 λ(γ) 和 β 要进行学习;
BatchNorm2d 适用于输入的数据为 4D,输入数据的形状 [N,C,H,W]
:N 表示批次,C 代表通道数,H 代表高度,W 代表宽度
网络模型调优的思路
对输入数据进行标准化
调整优化方法
调整学习率
增加批量归一化层
增加网络层数、神经元个数
增加训练轮数
数据再清洗,进行预处理
等等…
心得:通过对神经网络的学习,了解到了神经网络虽然功能强大,但深度学习较机器学习来说特征可解释性弱