提及线性学习,我们首先会想到线性回归。回归跟分类的区别在于要预测的目标函数是连续值

线性回归假定输入空间到输出空间的函数映射成线性关系,但现实应用中,很多问题都是非线性的。为拓展其应用场景,我们可以将线性回归的预测值做一个非线性的函数变化去逼近真实值,这样得到的模型统称为广义线性回归(generalized linearregression) :
y= g(wTx +b)
其中g(.)称为联系函数(link function)
理论上,联系函数9(·)可以是任意函数,比如当g(.)被指定为指数函数时,得到的回归模型称为对数线性回归
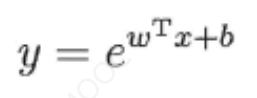
之所以叫对数线性回归,是因为它将真实值的对数作为线性回归逼近的目标,即:

为了简化,我们先考虑二分类任务,其输出标记y ∈{0,1},但线性回归模型产生的预测值: z= wTx +b
是实值,因此,我们需将实值z转换为0/1值。
最容易想到的联系函数g(.)当然是单位阶跃函数

但单位阶跃函数不连续,因此不能直接用作联系函数g(.)。于是我们希望找到能在一定程度上近似单位阶跃函数的替代函数,并希望它在临界点连续且单调可微。逻辑斯蒂函数(logistic function)正是这样一个常用的替代函数:

逻辑斯蒂(logistic function)函数形似s,是Siionnoid函数的典型代表,它将z值转化为一个接近0或1的y值,并且其输出值在z=O附近变化很陡。
其对应的模型称为逻辑斯蒂回归(logistic regression)。需要特别说明的是,虽然它的名字是“回归”,但实际上却是一种分类学习方法。
逻辑斯蒂回归有很多优点:
1)可以直接对分类可能性进行预测,将y视为样本x作为正例的概率;
2)无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题;
3)是任意阶可导的凸函数,可直接应用现有数值优化算法求取最优解。


逻辑斯蒂回归只能求解连续属性值问题,不能求解离散属性值问题,对于离散属性值的处理:
√若属性值之间存在“序”关系:
通过连续化将其转化为连续值
√若属性值之间不存在“序”关系:
通常可将k个属性值转换为k维向量
前面讲到的都是二分类学习任务,现实应用中常常会遇到多分类学习任务。
多分类学习方法:

拆分策略
√一对一 (One vs. One, OvO)
√一对其余( One vs.Rest, OvR)
√多对多(Many vs. Many, MvM)

预测性能取决于具体数据分布,多数情况下两者差不多


多对多(Many vs Many,MvM)
√若干类作为正类,若干个其他类作为反类
√纠错输出码(Error Correcting Output Code,ECOC)

对分类器错误有一定容忍和修正能力,编码越长、纠错能力越强
对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强