题目描述：

给你一个大小为 n x n 的整数矩阵 grid 。

生成一个大小为 (n - 2) x (n - 2) 的整数矩阵  maxLocal ，并满足：

    maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。

换句话说，我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。

返回生成的矩阵。

初始代码：

class Solution {
    public int[][] largestLocal(int[][] grid) {

    }
}

示例1：

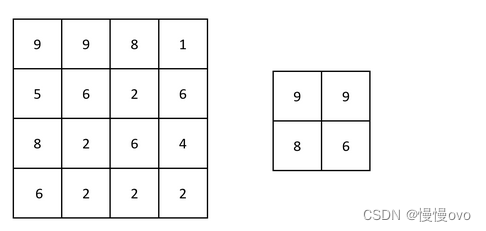
输入：grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出：[[9,9],[8,6]]
解释：原矩阵和生成的矩阵如上图所示。
注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例2：

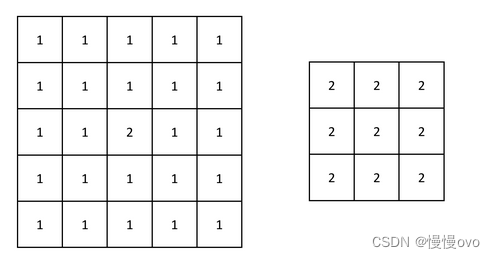
输入：grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出：[[2,2,2],[2,2,2],[2,2,2]]
解释：注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

参考答案：

class Solution {
    public int[][] largestLocal(int[][] grid) {
        int n = grid.length;
        int[][] maxLocal = new int[n - 2][n - 2];
        //遍历maxLocal进行填充
        for(int i = 0; i < n - 2;++i){
            for(int j = 0; j < n - 2;++j){
                maxLocal[i][j] = maxMethod(grid,i,j);
            }
        }
        return maxLocal;
    }

    /**
     * 以当前点为3 * 3为矩阵中心遍历返回其中最大值
     * grid 当前点作为矩阵中心的矩阵
     * m 往右移
     * n 往下移
     * return 矩阵中心的最大值
     */
    private int maxMethod(int[][] grid, int m, int n){
        int max = 0;//作为比较的初始值
        for(int i = m; i < m + 3;++i){
            for(int j = n; j < n + 3;++j){
                max = Math.max(max, grid[i][j]);
            }
        }
        return max;
    }
}