同向双指针的理解

双指针从同一侧开始走
一般是right进行无脑遍历，left控制边界（导致模板化）
深刻理解题目概念以及**（right - left +1）** 的含义
多思考画图

模板

class Solution {
public:
    int numSubarrayProductLessThanK(vector<int>& nums, int k) {
        int count = 0;
        int left = 0;
        for(int right=0; right<nums.size(); right++)
        {
            while() // 条件自己加
            {
            }
            count += right - left + 1;
        }
        return count;
    }
};

具体还是要以题目为例

leetcode 713

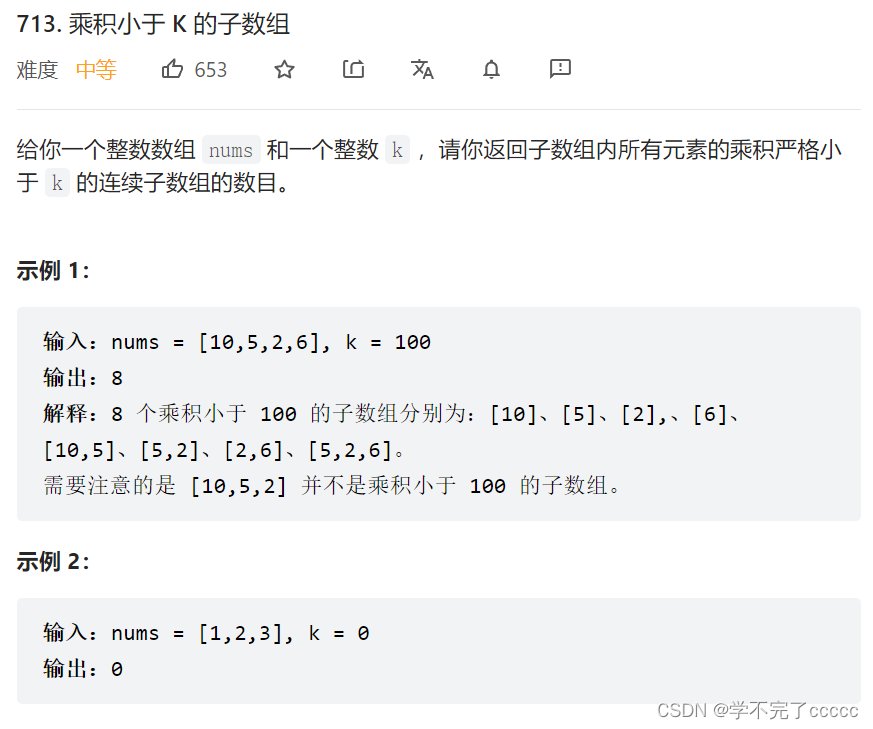
在这里插入图片描述

几个关键点

是正整数组
要找连续子数组（同向双指针）

代码示例

完全模板化编程

class Solution {
public:
    int numSubarrayProductLessThanK(vector<int>& nums, int k) {
        int count = 0;
        int left = 0;
        int mul = 1;
        for(int right=0; right<nums.size(); right++)
        {
            mul *=nums[right];
            while(left<=right && mul>=k)
            {
                mul /= nums[left++];
            }
            count += right - left + 1;
        }
        return count;
    }
};

leetcode 3

在这里插入图片描述
几个关键点

子串即连续子数组（同向双指针）
不含有重复字符（letf与right中间的子串一定是不含有重复字母的）

代码示例

还是模板化的

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int left = 0;
        int max_size = 0;
        unordered_map<char, int> tmap;
        for(int right=0; right<s.size(); right++)
        {
            tmap[s[right]]++;
            while(tmap[s[right]]>1)
            {
                tmap[s[left]]--;
                left++;
            }
            max_size = max_size < right - left+1 ? right-left+1 : max_size;
        }
        return max_size;
    }
};

leetcode 1004

在这里插入图片描述
几个关键点

返回连续1的个数即也是一个子串问题
滑动窗口之中永远是满足条件的1的个数

代码示例

class Solution {
public:
    int longestOnes(vector<int>& nums, int k) {
        int left = 0;
        int count = 0;
        int res = 0;
        for(int right=0; right<nums.size(); right++)
        {
            count += 1 - nums[right];
            while(count > k)
            {
                count -= 1 - nums[left];
                left++;
            }
            res  = res > right - left + 1 ? res : right - left + 1;
        }
        return res;
    }
};

leetcode 1234

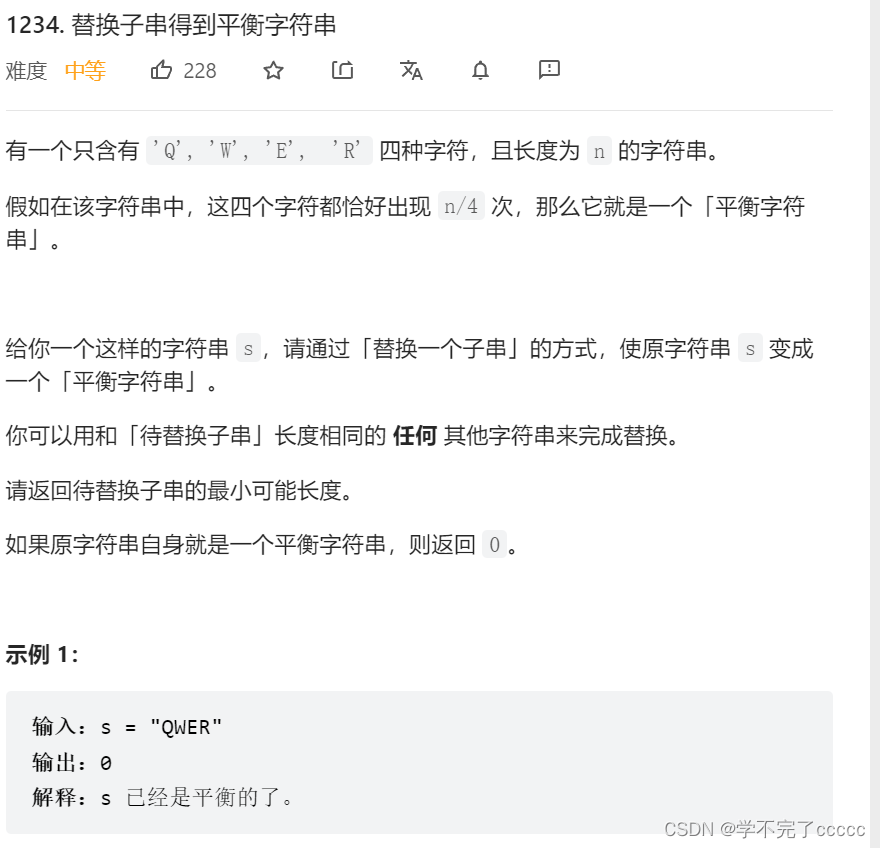
在这里插入图片描述
这道题核心我觉得是看清题目的意思
几个关键点

是用替换子串的方式进行变换（子串即同向双指针）
滑动窗口之外的各个字符数量<=m的话就可以通过替换（窗口内有>m的就不能替换）
不断更新最小值即可

代码示例

class Solution {
public:
    int balancedString(string s) {
        int n = s.length();
        int m = n / 4;
        unordered_map<char, int> tmap;
        for(int i=0; i<s.size(); i++)
        {
            ++tmap[s[i]];
        }
        if (tmap['Q'] == m && tmap['W'] == m && tmap['E'] == m && tmap['R'] == m)
            return 0; 
        int res = n, left = 0;
        for (int right = 0; right < n; right++) { // 枚举子串右端点
            --tmap[s[right]];
            // 判断窗口外的情况
            while (tmap['Q'] <= m && tmap['W'] <= m && tmap['E'] <= m && tmap['R'] <= m) {
                res = min(res, right - left + 1);
                ++tmap[s[left++]]; // 缩小子串
            }
        }
        return res;
    }
};