一：数组理论基础

首先要知道数组在内存中的存储方式，这样才能真正理解数组相关的题

数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

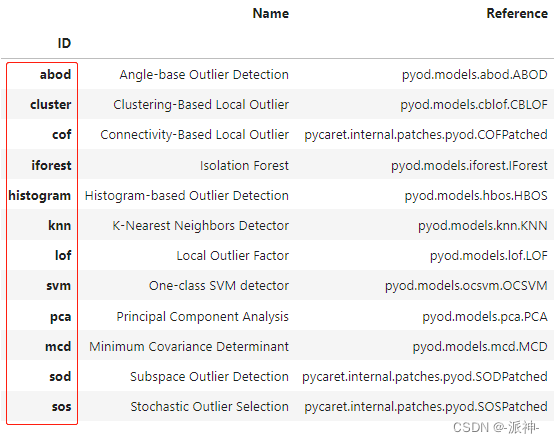
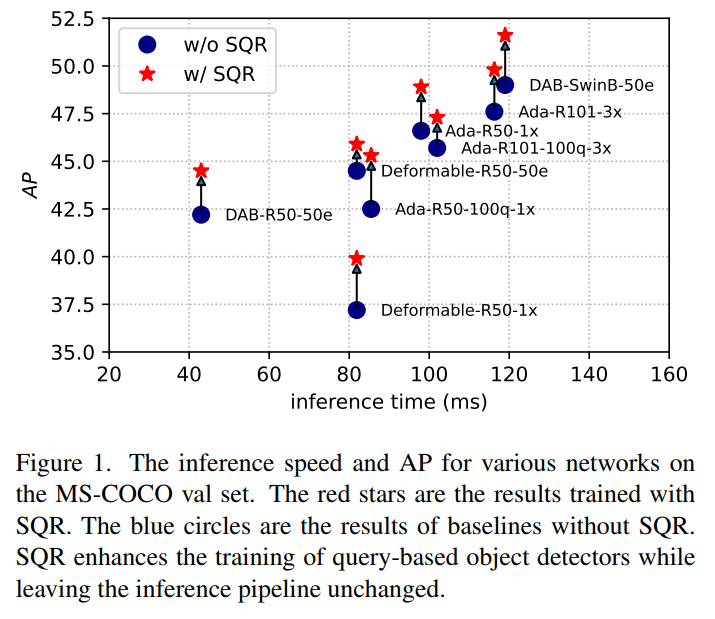
举一个字符数组的例子，如图所示：

需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

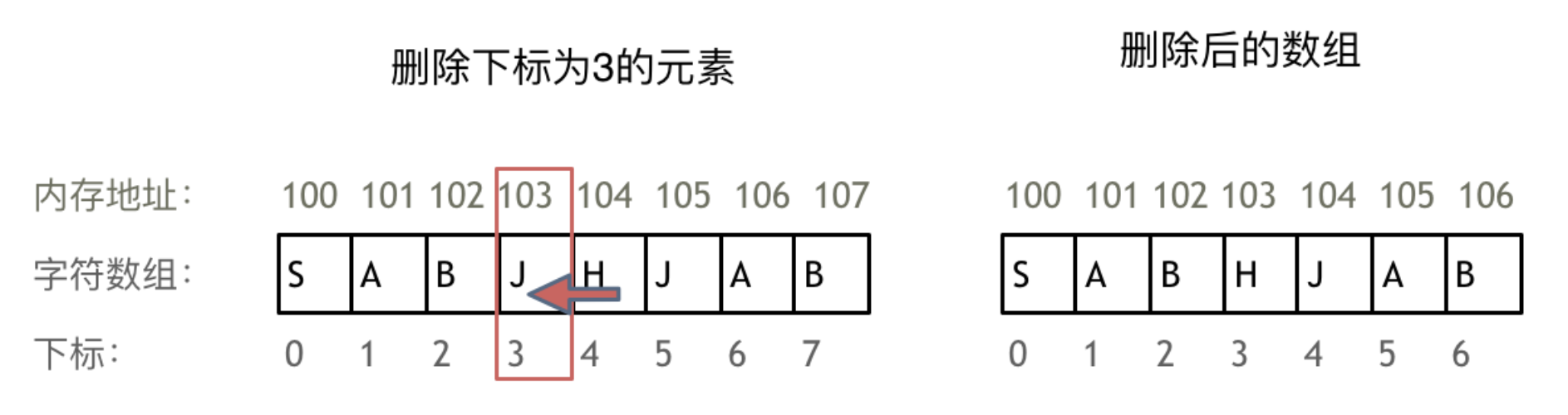
正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

二：数组知识点总结

1、数组当中可以存储“基本数据类型”的数据，也可以存储“引用数据类型”的数据。

2、数组因为是引用类型，所以数组对象存储在 堆内存 当中。（数组是存储在堆当中的）

3、数组当中如果存储的是“java对象”的话，实际上存储的是对象的“引用（内存地址）”，数组中不能直接存储java对象。

4、所有的数组对象都有 length 属性(java自带的)，用来获取数组中元素的个数。

5、java中的数组要求数组中元素的 类型统一。

比如：int类型数组只能存储int类型，Person类型数组只能存储Person类型。

6、数组在内存方面存储的时候，数组中的元素内存地址(存储的每一个元素都是有规则的挨着排列的)是连续的。内存地址连续。（数组特点）

7、所有的数组都是拿“第一个小方框的内存地址”作为整个数组对象的内存地址。
（数组中首元素的内存地址作为整个数组对象的内存地址。）

8、数组中每一个元素都是有下标的，下标从0开始，以1递增。最后一个元素的下标是：length - 1

三：数组这种数据结构的优点和缺点是什么？

优点：查询/查找/检索某个下标上的元素时效率极高。
原因：

第一：每一个元素的内存地址在空间存储上是连续的。

第二：每一个元素类型相同，所以占用空间大小一样。

第三：知道第一个元素内存地址，知道每一个元素占用空间的大小，又知道下标，所以通过一个数学表达式就可以计算出某个下标上元素的内存地址。直接通过内存地址定位元素，所以数组的检索效率是最高的。
注意：

缺点：
第一：由于为了保证数组中每个元素的内存地址连续，所以在数组上随机删除或者增加元素的时候，效率较低，因为随机增删元素会涉及到后面元素统一向前或者向后位移的操作。
第二：数组不能存储大数据量。
因为很难在内存空间上找到一块特别大的连续的内存空间。
注意：
对于数组中最后一个元素的增删，是没有效率影响的。

四：实战解题

1. 移除元素

力扣链接

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

暴力解法

这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

很明显暴力解法的时间复杂度是O(n^2)，这道题目暴力解法在leetcode上是可以过的。

代码如下：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
                size--; // 此时数组的大小-1
            }
        }
        return size;

    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

双指针法

思路及算法
由于题目要求删除数组中等于val的元素，因此输出数组的长度一定小于等于输入数组的长度，我们可以把输出的数组直接写在输入数组上。可以使用双指针:右指针right指向当前将要处理的元素，左指针left指向下一个将要赋值的位置。

·如果右指针指向的元素不等于val，它一定是输出数组的一个元素，我们就将右指针指向的元素复制到左指针位置，然后将左右指针同时右移;

·如果右指针指向的元素等于val，它不能在输出数组里，此时左指针不动，右指针右移一位。

整个过程保持不变的性质是:区间[0, left)中的元素都不等于value。当左右指针遍历完输入数组以后，left的值就是输出数组的长度。
这样的算法在最坏情况下(输入数组中没有元素等于value)，左右指针各遍历了数组一次。

class Solution {
    public int removeElement(int[] nums, int val) {
        // 快慢指针
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        return slowIndex;
    }
}

2.有序数组的平方

力扣链接

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

暴力解法

最直观的想法，莫过于：每个数平方之后，排个序，美滋滋，代码如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        for (int i = 0; i < A.size(); i++) {
            A[i] *= A[i];
        }
        sort(A.begin(), A.end()); // 快速排序
        return A;
    }
};

这个时间复杂度是 O(n + nlogn)， 可以说是O(nlogn)的时间复杂度，但为了和下面双指针法算法时间复杂度有鲜明对比，我记为 O(n + nlog n)。

双指针法

数组其实是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

class Solution {
    public int[] sortedSquares(int[] nums) {
        int right = nums.length - 1;
        int left = 0;
        int[] result = new int[nums.length];
        int index = result.length - 1;
        while (left <= right) {
            if (nums[left] * nums[left] > nums[right] * nums[right]) {
                // 正数的相对位置是不变的， 需要调整的是负数平方后的相对位置
                result[index--] = nums[left] * nums[left];
                ++left;
            } else {
                result[index--] = nums[right] * nums[right];
                --right;
            }
        }
        return result;
    }
}

最后说一句

感谢大家的阅读，文章通过网络资源与自己的学习过程整理出来，希望能帮助到大家。

才疏学浅，难免会有纰漏，如果你发现了错误的地方，可以提出来，我会对其加以修改。