写在开头

二分查找应该是算比较简单的这种算法了，我本以为还可以。但有时候也没想到过能这么用，最震惊的就是对答案进行二分了。而且有时候不够熟练，还有我遇到的问题都总结一下。

算法前提：

数据需要有序，可以重复元素。

算法逻辑

以升序数列为例，
比较一个元素与数列中的中间位置的元素的大小
1.如果比中间位置的元素大，则继续在后半部分的数列中进行二分查找；
2.如果比中间位置的元素小，则在数列的前半部分进行比较；
3.如果相等，则找到了元素的位置。
每次比较的数列长度都会是之前数列的一半，直到找到相等元素的位置或者最终没有找到要找的元素。

算法实现

简单实现

// 二分查找
public static int binarySearch(int[] a, int target) {
    int left = 0;
    int right = a.length - 1;
     while (left <= right) {
        int mid = (left + right) / 2;
        if (a[mid] == target) {
            return mid;
        } else if (a[mid] < target) {
            left = mid + 1;
        } else {
           right = mid - 1;
       }
   }
   return -1; 
}

left+right可能超过int表示的最大限度

出现结果：mid算出来为负数。
java中int类型占4个字节的最大值是 $2^{31}-1$, 即 2147483647
如果超过了表示范围，则会发送越界，则会加到符号位。
那么我们可以进行无符号右移就可以完成除法运算，和解决越界问题了。
（有没有可能超过32位，2个int数相加最大不会大于$2^{32}-1$，所以一定不会超过int存储）
所以代码修改如下

int mid =(left+right)>>>2;

代码分析和变换

简单实现里面：还是建议把等值放到最后面，因为等值的可能性是最低的，这样也就可以降低判断的次数。
把谁放第一判断，则那一边效率会高一点，如果下代码，如果数据偏右，则效率可能高些。

if (a[mid] < target) {
     left = mid + 1;
} else if (a[mid] > target) {
    right = mid - 1;
} else {
   return mid;
}

最坏情况$O(\log n)$
最好情况$O(1)$
空间复杂度$O(1)$

均衡性:每次循环必定需要一次判断

public static int binarySearch(int[] a, int target) {
    int left = 0;
    int right = a.length;
     while (right - left <= 1) {
        int mid = (left + right) / 2;
        if (target < a[mid]) {
            right = mid;
        } else{
            left = mid;
        }
       }
       return a[i]==target?i:-1;
   }
   return -1; 
}

时间复杂度$\Omega (\log n)$

更多需求：求索引最小的值

public static int binarySearchMin(int[] a, int target){
	int l=0,r=a.length;
	while(l < r){
		int m = (l + r) >>> 1;
		if (a[m] < target)
			l = m + 1;
		else
			r = m;
	}
	return l;
}

注意：如果数据不存在则返回的是切入点
不想这样的话可以

return a[l]==target?l:-(l+1);

java二分API

在Arrays类中有一个binarySearch()的方法可以返回数组中二分查找的结果
使用：

binarySearch(数组，key)

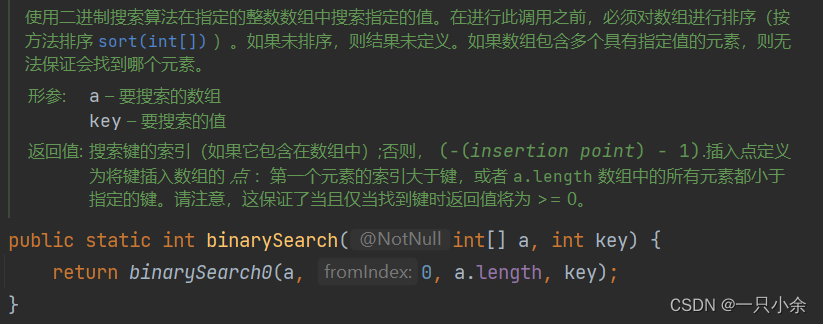
源代码：和我们实现的差不多。

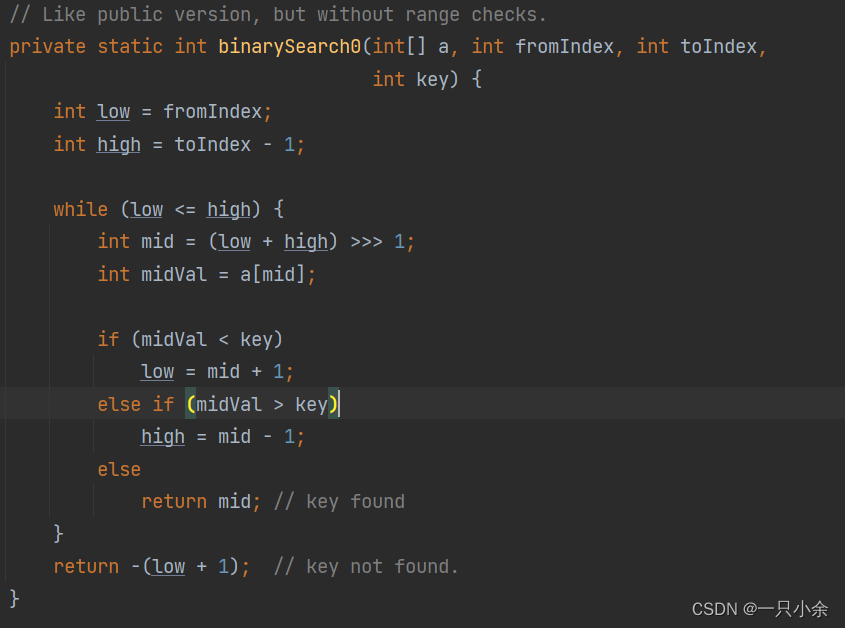
格外的api

public static int binarySearch(int[] a, int fromIndex, int toIndex,int key)
fromIndex – 要搜索的第一个元素（包括）的索引 
toIndex – 要搜索的最后一个元素（独占）的索引

应用

基础题

力扣278. 第一个错误的版本
解决：二分求索引最小

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int l=1;int r=n;
        while(l < r){
            int mid=(l+r)>>>1;
            if(isBadVersion(mid))
                r=mid;
            else
                l=mid+1;
        }
        return l;
    }
}

leetcode34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。

public int[] searchRange(int[] nums, int target) {
        int x = -1, y = -1;
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int m = (l + r) >>> 1;
            if (nums[m] >= target)
                r = m;
            else
                l = m + 1;
        }
        if (l < 0 || l > nums.length-1||nums[l] != target)
            return new int[]{x, y};
        x = l;
        r = nums.length - 1;
        while (l < r) {
            int m = (l + r) >>> 1;
            if (nums[m] > target)
                r = m - 1;
            else
                l = m + 1;
        }
        y = l - 1;
        return new int[]{x, y};
    }

思考难度

leetcode 4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数.
算法的时间复杂度应该为 O(log(m+n)) 。

分析：
l=n+m为总数
求中位数：

1. 如果l为奇数，则中位数为(l+1)/2的位置
2. 如果为偶数，则中位数为(l+1)/2和(l+2)/2的平均数

即求指定位置k的数。

在每次比较k/2位置的2个数组上的数如果n1[k/2]<n2[k/2]则n1上k/2以前的数都在合并k位置之前。
如：
n1=[1,2,4,5,6]
n2=[2,3,5,7,9,11]
l=11 k=6 k/2=3
n1[3]=4<n2[3]=5
则1，2，4都会在合并数组k位置的前面

n1=[5,6]
n2[2,3,5,7,9,11]
此时k=3 k/2=1
比较5和2

所以
n1=[5,6]
n2[3.5,7,9,11]
此时k=2,k/2=1
去掉一个3

k=1
返回2个最开始的小值就行。

问：
1.能不能在k=2的时候返回大值呢？
不行的，如果一个数组1，2另一个3，4就不可用。
2.如果k/2大于一个数组长度呢？
那就取这个数组最后一个就行了，这样要么不用考虑这个数组了，要么长数组会变短。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int m = nums2.length;
    int left = (n + m + 1) / 2;
    int right = (n + m + 2) / 2;
    //将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k 。
    return (search(nums1, 0, nums2, 0, left) + search(nums1, 0, nums2, 0, right)) * 0.5; 
}
// a为一个数组，i为这个数组剩下的.b同理
// k 为需要求的数的位置
public int search(int[] a,int i,int[] b,int j,int k){
	//求剩余长度
	int l1 = a.length-i;
	int l2 = b.length-j;
	//调整l1永远为短的
	if(l1>l2) return search(b,j,a,i,k);
	
	if(l1 == 0) return b[j+k-1];
	if (k == 1) return Math.min(a[i], b[j]);
	int q = k/2;
	//x,y 为索引
	int x = i + Math.min(q,l1) - 1;
	int y = j + Math.min(q,l2) - 1;

	if(a[x] > b[y])
		return search(a,i,b,y+1,k-(y-j+1));
	else
		return search(a,x+1,b,j,k-(x-i+1));
}

方法

leetcode2439. 最小化数组中的最大值
给你一个下标从 0 开始的数组 nums ，它含有 n 个非负整数。
每一步操作中，你需要：
选择一个满足 1 <= i < n 的整数 i ，且 nums[i] > 0 。
将 nums[i] 减 1 。
将 nums[i - 1] 加 1 。
你可以对数组执行任意次上述操作，请你返回可以得到的 nums 数组中最大值最小为多少。

示例 1：

输入：nums = [3,7,1,6]
输出：5
解释：
一串最优操作是：
1. 选择 i = 1 ，nums 变为 [4,6,1,6] 。
2. 选择 i = 3 ，nums 变为 [4,6,2,5] 。
3. 选择 i = 1 ，nums 变为 [5,5,2,5] 。
nums 中最大值为 5 。无法得到比 5 更小的最大值。
所以我们返回 5 。

示例 2：

输入：nums = [10,1]
输出：10
解释：
最优解是不改动 nums ，10 是最大值，所以返回 10 。

提示：
$n==nums.length$
$2<=n<=10^5$
$0<=nums[i]<=10^9$

分析：
这个题目是我第一次遇到二分答案的题目，属实打开了我的新世界了。
对答案进行二分。
1.根据题目要求右边只能降，左边只能升。第一个值可以从后面所有的值里面取过来。
2.所以对一个最大值m是否符合条件，我们可以从左往右遍历，如果这个数k比他小那么，则需要m-k个位置，如果比他大，那么把需要减掉，这时如果需求为负数，则一定不是这个数。

但是最大值如果很大，那么都会是需要位置而没有剪掉的呢？
因为我们二分会去找最小可能，即找到符合的最左边就行。

public int minimizeArrayValue(int[] nums) {
	int l = 0,r = Integer.MAX_VALUE;
	while(l < r){
		int m = (l+r)>>>1;
		if(check(nums,m))
			r = m;
		else
			l = m+1;
	}
	return r;
}
public static boolean check(int[]a,int m){
	long count = 0;
	for(int i:a){
		if(i<m)
			count+=m-i;
		else{
			count -= i-m;
			if(count < 0)
			return false;
		}
	}
	return true;
}