题目描述：给定一棵二叉树(结构如下)，其中每个节点值为整数。给定一个值 K，求所有满足如下条件的路径并将路径上节点的值打印出来：

        1、路径方向必须向下，即只能从父节点指向子节点

        2、路径并不是必须从根节点开始或在叶节点结束。即树上任意节点开始向下走到任意节点的路径都 允许。

        3、路径上的节点得分之和等于给定值 K。节点得分=节点值+节点所在层(根节点为 0，之后每层+1)。

示例：给定二叉树[5,3,7,9,null,11,2,4,-1, null,null,2,-2]，K=16

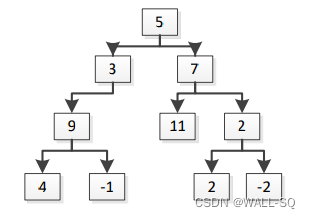
输出：

5 3 9 -1

5 7 2 2

3 9 4

解释：如第一个路径 5 3 9 -1，路径上节点得分分别为 5+0,3+1,9+2,-1+3,和为 22

输入格式：第一行为一个整数 K，第二行为一个二叉树的层次遍历序列，其中空子树用 null 表示，每两个数字或者 null 之间用空格分隔，例如:

22

5 3 7 9 null 11 2 4 -1 null null 2 -2

需要注意的是，null 节点的子节点不会显式的写出来，如上例中第二行值为 3 的节点的右子树为空， 则该右空子树的左右子树不会再以 null 表示。

输出格式：分为多行，每行为一个满足条件的路径上节点的值的序列，例如:

5 3 9 -1

5 7 2 2

3 9 4

现有如下输入：

35

5 4 8 11 null 13 4 7 2 null null 5 1 8 null 7 10 6 null null null 

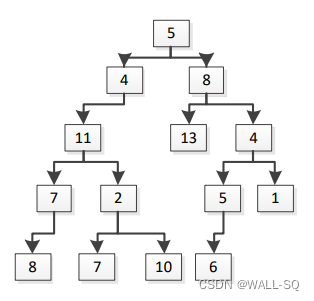
请用程序将正确结果输出

思路：我们先弱化问题，如果我们现在已经有一棵建好的树，此时要我们输出树上所有向下路径和为K的路径；为了解决这个问题，我们再弱化问题，假设只要求从根节点出发的路径，那么从根节点开始，我们当前的路径和为根节点的val值，已经经过的节点为根节点，下一步我们可以选择的是向左或者向右，那么对于后续的节点，也是一样的，这样其实就是一个DFS问题。为了能够输出和为K的路径，我们需要sum存储当前和路径和以及一个容器vector存储当前经历过的节点。我们的DFS雏形就有了 DFS(TreeNode* root, int sum, vector<int> nums)。 

现在我们强化条件，回到不要求从根节点出发，我们增加一个mark位，用于指示现在是否是在路径内，如果在路径内，那么当前遍历到的节点值必须累加，并加其加入路径节点的容器，否则的话，可以选择不加，也可以选择加，DFS变为 DFS(TreeNode* root, int sum, vector<int> nums. bool in_path)。

现在还剩下最后一个建树的问题了，既然是BFS序那么直接按照BFS的方式建树就好啦。

#include<bits/stdc++.h>
using namespace std; 

struct Node{
	int num;
	Node *lchild, *rchild;
	bool have_l = false, have_r = false; //由于我们没有办法通过lchild、rchild是否为null判断是否有孩子，所以需要手动设置标记位
	Node(int num, Node *lchild, Node *rchild){
		this -> num = num;
		this -> lchild = lchild;
		this -> rchild = rchild;
	}
};

void DFS(Node* root, bool start, int sum, vector<int>& choices, int k){
	if(!root){
		return;
	}
	if(!start){//如果路径还没开始，则当前节点可以选择不加入
		DFS(root -> lchild, false, 0, choices, k);
		DFS(root -> rchild, false, 0, choices, k);
	}
	sum = sum + root ->num;//累计上当前节点
	choices.push_back(root -> num);
	if(sum == k){
		for(int choice:choices){
			cout << choice << " ";
		}
		cout << endl;
	}
	DFS(root -> lchild, true, sum, choices, k);
	DFS(root -> rchild, true, sum, choices, k);
	choices.pop_back();
}

int main(){
	int k, num;
	Node *root = NULL, *fa=NULL;
	queue<Node*> que;
	cin >> k;
	string input;
	while(cin >> input){
		if(input == "null"){
			num = 0x3f3f3f3f;//用于标记该节点为无效值 应生成NULL
		}else{
			stringstream ss(input);
			ss >> num;
		}
		if(root == NULL){//没有根节点则先建立根节点
			root = new Node{num, NULL, NULL};
			que.push(root);
		}else{//如果有父节点则先判断当前根节点是否已经挂好孩子，如果没有则挂孩子，否则取下一个父节点
			if(fa == NULL || fa -> have_r){//还未设置父亲(上一步刚建立根节点)或者父亲的子节点都已经满了 重新取一个 
				fa = que.front();
				que.pop();
			}
			Node* son = num == 0x3f3f3f3f ? NULL : new Node{num, NULL, NULL};
			if(son != NULL){
				que.push(son);
			}
			if(fa -> have_l == false){//如果父节点的左孩子没有挂节点，则挂节点
				fa -> lchild = son;
				fa -> have_l = true;
			}else{//否则此时应该挂右节点
				fa -> rchild = son;
				fa -> have_r = true;
			}
		}
	}
	vector<int> choices;
	DFS(root, false, 0, choices, k);
	return 0;
} 

注：本方法还不能完全去掉重复路径，因为可能存在路径节点不同但是路径上的值都相同的情况，如下

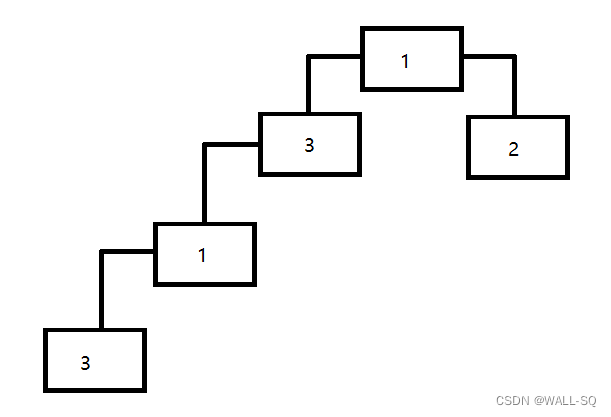
此时存在两条1-3的路径，如果题目要求不能一点重复，则可以选择使用hash_set的方式，对于路径1-3，可以进行如下方式的存储 - 1#3#，需要#作为分隔符是为了防止出现诸如值为13的节点导致路径1-3(两个节点)和路径13(一个节点)无法区分的情况。

oh...no!!!我们看丢了一个条件，节点得分=节点值+节点所在层(根节点为 0，之后每层+1)。

但是我们在当前代码的基础上小改一下即可，有两种修改方式

1. 在节点建立的过程中直接增加层次

2. 在DFS的过程中增加floor表明层数

二者均可，读者请自行斟酌，本人这里简单起见用第二种

#include<bits/stdc++.h>
using namespace std; 

struct Node{
	int num;
	Node *lchild, *rchild;
	bool have_l = false, have_r = false; //由于我们没有办法通过lchild、rchild是否为null判断是否有孩子，所以需要手动设置标记位
	Node(int num, Node *lchild, Node *rchild){
		this -> num = num;
		this -> lchild = lchild;
		this -> rchild = rchild;
	}
};

void DFS(Node* root, bool start, int sum, vector<int>& choices, int floor, int k){
	if(!root){
		return;
	}
	if(!start){//如果路径还没开始，则当前节点可以选择不加入
		DFS(root -> lchild, false, 0, choices, floor + 1, k);
		DFS(root -> rchild, false, 0, choices, floor + 1, k);
	}
	sum = sum + root ->num + floor;//累计上当前节点
	choices.push_back(root -> num);
	if(sum == k){
		for(int choice:choices){
			cout << choice << " ";
		}
		cout << endl;
	}
	DFS(root -> lchild, true, sum, choices, floor + 1, k);
	DFS(root -> rchild, true, sum, choices, floor + 1, k);
	choices.pop_back();
}

int main(){
	int k, num;
	Node *root = NULL, *fa=NULL;
	queue<Node*> que;
	cin >> k;
	string input;
	while(cin >> input){
		if(input == "null"){
			num = 0x3f3f3f3f;//用于标记该节点为无效值 应生成NULL
		}else{
			stringstream ss(input);
			ss >> num;
		}
		if(root == NULL){//没有根节点则先建立根节点
			root = new Node{num, NULL, NULL};
			que.push(root);
		}else{//如果有父节点则先判断当前根节点是否已经挂好孩子，如果没有则挂孩子，否则取下一个父节点
			if(fa == NULL || fa -> have_r){//还未设置父亲(上一步刚建立根节点)或者父亲的子节点都已经满了 重新取一个 
				fa = que.front();
				que.pop();
			}
			Node* son = num == 0x3f3f3f3f ? NULL : new Node{num, NULL, NULL};
			if(son != NULL){
				que.push(son);
			}
			if(fa -> have_l == false){//如果父节点的左孩子没有挂节点，则挂节点
				fa -> lchild = son;
				fa -> have_l = true;
			}else{//否则此时应该挂右节点
				fa -> rchild = son;
				fa -> have_r = true;
			}
		}
	}
	vector<int> choices;
	DFS(root, false, 0, choices, 0, k);
	return 0;
}