二分找最左边

核心思想: 先mid =(l+r)/2每次向左取整; 然后命中target的时候，右边界逼近到mid;

因为每次mid向左取整，mid命中target时l代替mid位置，则循环迭代最后会卡出重复数字最左侧的位置！

可以用int arr[5] = 3 3 3 3 3 ; int target = 3; 这种极端的用例，来方便理解一下上述二分算法！

 //二分找k的最左侧位置
        while(l<r)
        {
            mid =  (l+r)>>1; //mid向左取整
            if(arr[mid]>=target ) r = mid;//mid命中时右边界r代替mid位置(二分区间整体向左收缩了)
            else l = mid+1;
        }

寻找过程图示如下:

---

二分找最右边

核心思想: 先mid =(l+r+1)/2 每次向右取整; 然后命中target的时候，左边界逼近到mid;

因为每次mid向右取整，mid命中target时l代替mid位置，则循环迭代最后会卡出重复数字最右侧的位置！ 同上，不过多解释;

 //二分找target的最右侧位置
        while(l<r)
        {
            mid =  (l+r+1)>>1; //mid向右取整
            if(arr[mid]<=target ) l = mid;//mid命中时左边界l代替mid位置(二分区间整体向右收缩了)
            else r = mid-1;
        }

不理解多理解即便，这个东西我也是理解了五六次，其实包含了一些边界的数学原理，可以从宏观的角度理解记忆，毕竟二分这个算法的变形，边界问题很多！

---

综合应用(剑指offer)

数字在升序数组中出现的次数

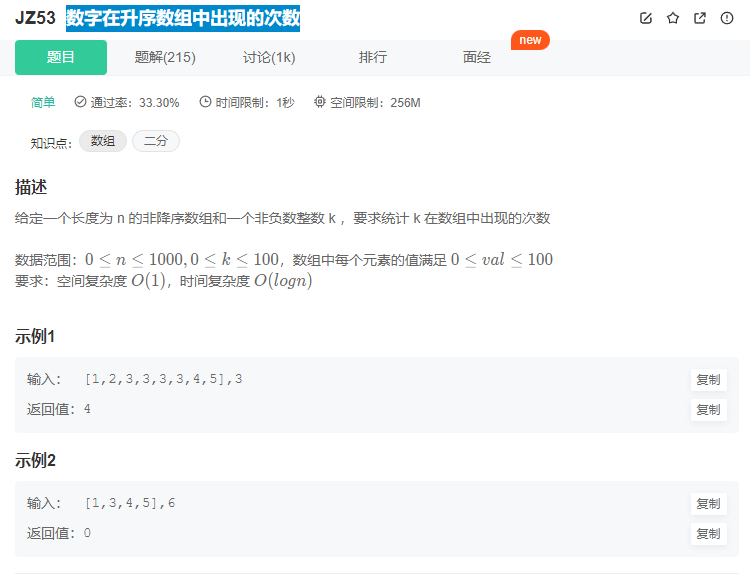
这道题要求O(logN)的时间复杂度，那肯定二分了！而且有序数组…这不是天然的二分有序条件吗;

题目解析

• 据观察，重复的数字在有序数组中出现的位置一定是互相挨着的:

• 那么我们只需要找到目标值k的最左侧下il标，和其最右侧下标ir，return ir-il+1; 即可！（当然，需要考虑一下k在数组中不存在的情况,这都是小问题啦）

怎么找最左侧和最右侧的k的下标，那就是上面设计的两种二分策略，需要掌握，常用！

实现代码

class Solution {
public:
    int GetNumberOfK(vector<int> data ,int k) {
        //二分找重复的最左 和 最右
        if(data.size()==0) return 0;
        int r = data.size() - 1;
        int l = 0;
        int mid;
        int il;
        int ir;
        //二分找k的最左侧位置
        while(l<r)
        {
            mid =  (l+r)>>1; //向左取整
            if(data[mid]>=k) r = mid;//命中时右边界也向左逼近
            else l = mid+1;
        }
        if(data[l]!=k) return 0;//特殊情况，k不存在，返回0;
        il = l;
        

       //二分找k的最右侧位置
        l = 0;
        r = data.size() - 1;
         while(l<r)
        {
            mid =  (l+r+1)>>1;//向右取整
            if(data[mid]<=k) l = mid;//命中时左边界也向右逼近
            else r = mid-1;
        }
        ir = l;

        return ir-il+1;
    }
};