线性代数学习-1
- 行图像和列图像
- 行图像
- 列图像
- 总结
本文转载于https://herosunly.blog.csdn.net/article/details/88698381
该文章本人认为十分有用,便自己敲一遍笔记加固印象
原文链接 原文
这个笔记感觉比我老师讲的更加透彻,清晰。很好的展示了线性代数的原理,强烈推荐看原文
行图像和列图像
线性方程的几何图像
线性代数的一个重要问题是求解n元一次方程组。例如下面的二元方程组
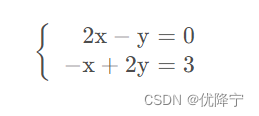
用矩阵表示如下所示:
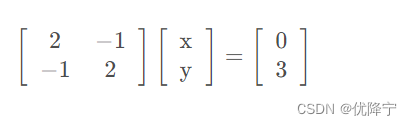
其中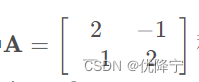 称为是系数矩阵,未知数向量
称为是系数矩阵,未知数向量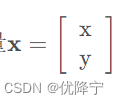 ,等号右侧的向量记为b。可得Ax=b
,等号右侧的向量记为b。可得Ax=b
行图像
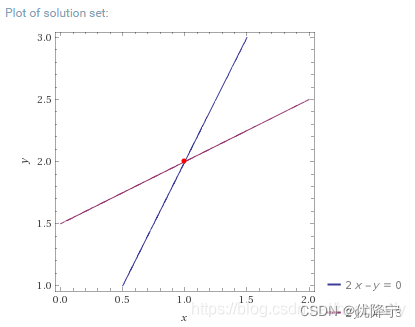
行图像和解析几何的结果是一致的,即每个方程的图像为一条直线。绘制出两个方程组对应的直线,两条直线交点即为方程组的解x=1,y=2。
列图像
在列图像中,我们将系数举证按列划分,即把矩阵分解成若干列向量的形式,则求解原方程可转化为为寻找列向量的线性组合来构成向量b。

向量的线性组合是课程的重要概念之一。其中线性组合指的是向量的加法和向量的数乘。其中向量的加法需满足平行四边形法则或者三角形法则,向量的数乘指的是向量的伸缩(其中系数大于1则进行伸展,小于1则进行收缩)。其中,基向量的线性组合能够表示整个空间。
从几何上讲,我们是寻找满足如下要求的x和y,是的两者分别数乘对应的列向量之后相加得到向量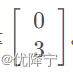
如果只是二元方程,可能还看不出来列图像的优势,如果是多元方程,就显而易见了。
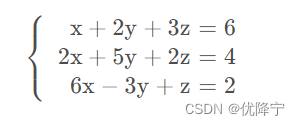
对于方程组Ax=b而言,如果改变等号右侧向量b的数值,那么对于行图像而言三个平面都改变了,而对于列图像而言,三个向量并没有发生改变,只是需要寻找一个新的组合
总结
1、行图像是将方程化成图像,而方程组组成的多个图像的交点就是方程组的解
2、列图像是将未知数的系数合并成一个列向量,用列向量来表示一个方程组