一、图的存储形式

---

线性表 中的元素 , 有 一个 直接前驱 和 一个 直接后继 ;

树 中的元素 , 有 一个 直接前驱 和 多个 直接后继 ;

图 中的元素 , 有 多个 直接前驱 和 多个 直接后继 ;

图 数据结构 中 , 每个 结点 是一个 元素 , 可以有 0 个或 多个 相邻元素 , 两个结点 之间的 连接 称为 边 ;

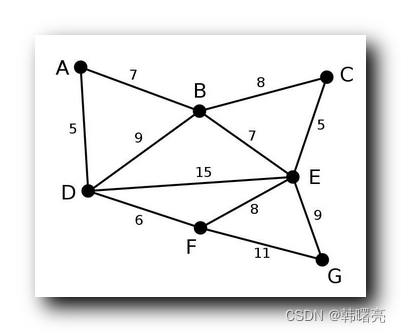
在下面的图中 , A ~ G 是结点 , 结点之间的连接是 边 , 每条边 可以有权重 ;

二、图的基本概念

---

图的基本概念 :

• 顶点 : 图中的 结点 ;
• 边 : 图中 结点 之间的边 ;
• 路径 : 边的权重 ;
• 图的分类 : 边的方向 ;
  • 无向图 : 结点之间的边 没有方向 ; 上图是一个无向图 ;
  • 有向图 : 结点之间的边 有方向 ; 节点之间的边有箭头 ;
  • 带权图 : 边 是有 权重 的 , 计算时不仅要计算路径 , 还要考虑路径的权重 ;

三、图的表示方式

---

图的表示方式 :

• 邻接矩阵 : 二维数组 ;
• 邻接表 : 链表 ;

1、邻接矩阵

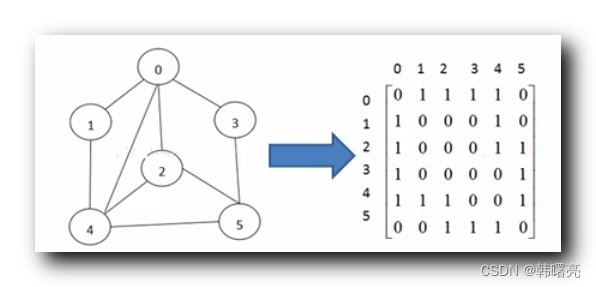
图 中有 6 个结点 , 0 ~ 5 ;

使用 6x6 的矩阵 表示 图 , 第 i 行 第 j 列 的元素表示 结点 i 和 结点 j 是否连接 ;

默认情况下 结点 与 结点 本身 没有连接 ;

第 0 行 第 1 列 值为 1 , 表示 结点 0 到 结点 1 之间 有边连接 ;
第 4 行 第 5 列 值为 1 , 表示 结点 4 到 结点 5 之间 有边连接 ;

2、邻接表

邻接矩阵 要 为 n 个顶点 分配 n x n 大小的空间 , 存储结点间的边是否存在 , 这样会造成一定的损失 ;

邻接表 中 , 只存储 存在的 边 , 不存储 不存在的 边 ;

邻接表 底层数据结构 由 数组 + 链表 组成 ;

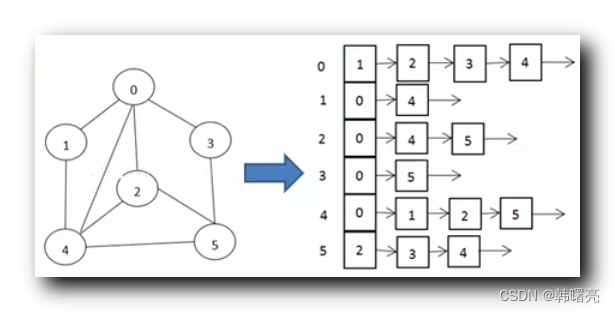
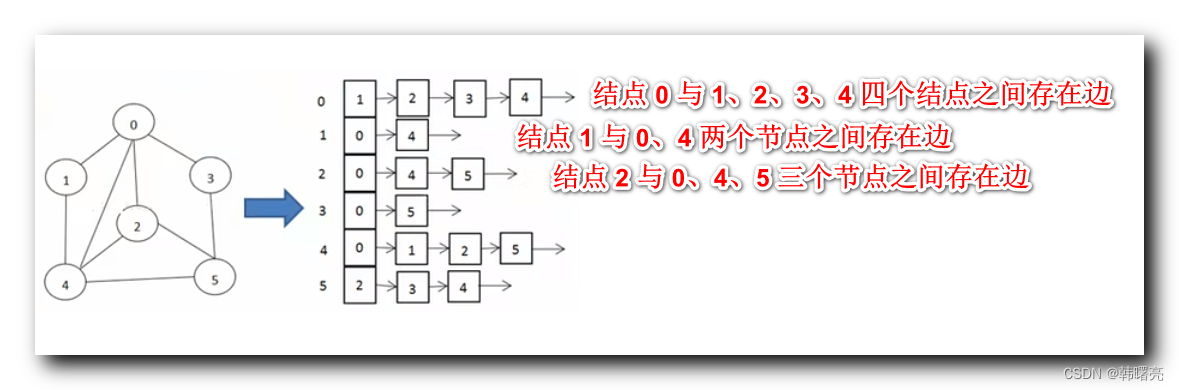
上图中 , 邻接表 左侧的 0 ~ 5 表示 标号为 0 ~ 5 之间的结点 ;

第一行 0 : 1 -> 2 -> 3 ->4 -> 表示 结点 0 与 1、2、3、4 四个结点之间存在边 ;

第二行 1 : 0 -> 4 -> 表示 结点 1 与 0、4 两个节点之间存在边 ;

第二行 2 : 0 -> 4 -> 5 -> 表示 结点 2 与 0、4、5 三个节点之间存在边 ;

四、图的创建 ( 代码示例 )

---

创建下图的数据结构 , 使用 邻接矩阵 表示图 ;

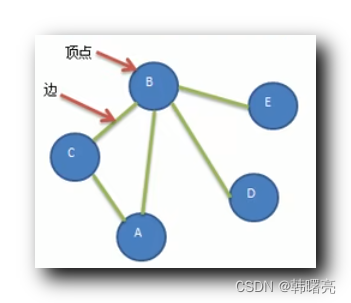
使用矩阵表示上图 :

$$\left[\begin{array}{cccccc}0& A& B& C& D& E\\ A& 0& 1& 1& 0& 0\\ B& 1& 0& 1& 1& 1\\ C& 1& 1& 0& 0& 0\\ D& 0& 1& 0& 0& 0\\ E& 0& 1& 0& 0& 0\end{array}\right]$$

数据结构分析 :

• 使用 ArrayList 存储顶点 ;
• 使用 int[][] 邻接矩阵 存储 图 ;

代码示例 :

import java.util.ArrayList;
import java.util.Arrays;

public class Graph {

    /**
     * 图顶点
     */
    private ArrayList<String> vertexList;

    /**
     * 图的邻接矩阵
     */
    private int[][] edges;

    /**
     * 图中边的数据
     */
    private int numOfEdges;

    /**
     *  构造器
     * @param n 顶点个数
     */
    public Graph(int n) {
        // 创建 n x n 邻接矩阵
        edges = new int[n][n];
        // 初始化顶点容器
        vertexList = new ArrayList<>(n);
        // 边数量统计
        numOfEdges = 0;
    }

    /**
     * 插入顶点
     * @param vertex 顶点名称
     */
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }

    /**
     * 插入边
     * @param v1 起始顶点索引
     * @param v2 终止顶点索引
     * @param weight 顶点的权重
     */
    public void insertEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;

        // 边的数量增加 1
        numOfEdges++;
    }

    /**
     * 获取结点个数
     * @return
     */
    public int getNumberOfVertex() {
        return vertexList.size();
    }

    /**
     * 获取边的个数
     * @return
     */
    public int getNumberOfEdges() {
        return numOfEdges;
    }

    /**
     * 获取指定节点的索引值
     * @param i
     * @return
     */
    public String getVertexByIndex(int i) {
        return vertexList.get(i);
    }

    /**
     * 获取 v1 到 v2 的权值
     * @param v1
     * @param v2
     * @return
     */
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }

    /**
     * 打印邻接矩阵
     */
    public void showGraph() {
        for (int i = 0; i < edges.length; i++) {
            System.out.println(Arrays.toString(edges[i]));
        }
    }

    public static void main(String[] args) {
        // 创建图
        Graph graph = new Graph(5);

        // 添加顶点
        graph.insertVertex("A");
        graph.insertVertex("B");
        graph.insertVertex("C");
        graph.insertVertex("D");
        graph.insertVertex("E");

        // 添加边
        graph.insertEdge(0, 1, 1);  // AB
        graph.insertEdge(0, 2, 1);  // AC

        graph.insertEdge(1, 0, 1);  // BA
        graph.insertEdge(1, 2, 1);  // BC
        graph.insertEdge(1, 3, 1);  // BD
        graph.insertEdge(1, 4, 1);  // BE

        graph.insertEdge(2, 1, 1);  // CA
        graph.insertEdge(2, 2, 1);  // CB

        graph.insertEdge(3, 1, 1);  // DB

        graph.insertEdge(4, 1, 1);  // EB

        // 打印临街矩阵
        graph.showGraph();
    }
}

执行结果 :

> Task :Graph.main()
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 1, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]