前言
这不单单是稀疏数组的开始,也是我重学数据结构的开始。因此,在开始说稀疏数组的具体内容之前,我想先说一下作为一个有着十余年“学龄”的学生,所一直沿用的一个学习方法:3W法。我认为,只有掌握了正确的学习方法,才能真正的达到“事半功倍”的境界。
何为3W?其实就是3问:What?Why?How?
简单解释一下:
1.What:界定问题,首先要搞清楚这个问题是什么。
若连题都读不懂,就不必说如何解题了。
2.Why:分析问题,要分析问题的本质和原因。
在读懂题意的前提下,知道它考察的方向是什么,这样后续才能顺着这个方向去解题。
3.How:解决问题,通过目标导向思维解决问题。
经过前两问的思考,想必你已经透过题目明白了这道题真正考察的是什么,那么就要考虑如何去处理、解决掉它。
1.What?
好,我们开始稀疏数组的具体内容。在了解为什么要学习它和怎样使用之前,我们要先了解稀疏数组是什么。
我们通过具体的应用场景来了解它,比如说,你用编程语言需要写一个简单的五子棋小游戏,它需要能够正常玩,并且有存盘和读取功能。
此时你能想到的问题就是:
- 如何绘制棋盘并存储棋盘上落子的坐标信息。
- 如何实现存盘和读盘的功能。
首先来思考第一个问题:总所周知,棋盘由行和列组成。那么,你很自然的想到了数学中的坐标系,将其落子点看做一组横纵坐标。因此你打算使用二维数组这一数据结构来模拟棋盘。用0代表没有落子,1代表落黑子,2代表落白字。
好,问题轻松写意地解决了。你开始写代码,作为一个有着程序员精神的人,你很快地通过百度解决了第二个问题。但你的程序员灵魂并不甘于止步于此,又想琢磨如何优化,此时迎来了一个新的问题:若一个11*11大小的棋盘,只落了两个子。此时需要存盘,如何才能尽可能多的节省存储空间?
很显然,若使用0来代表未落子的交点,那么这个二维数组中就有着许许多多的“无效数据”。只有当黑子 / 白子落在这个交点上,它才是“有效数据”。此时,稀疏数组就出现在你的面前了。
2.Why?
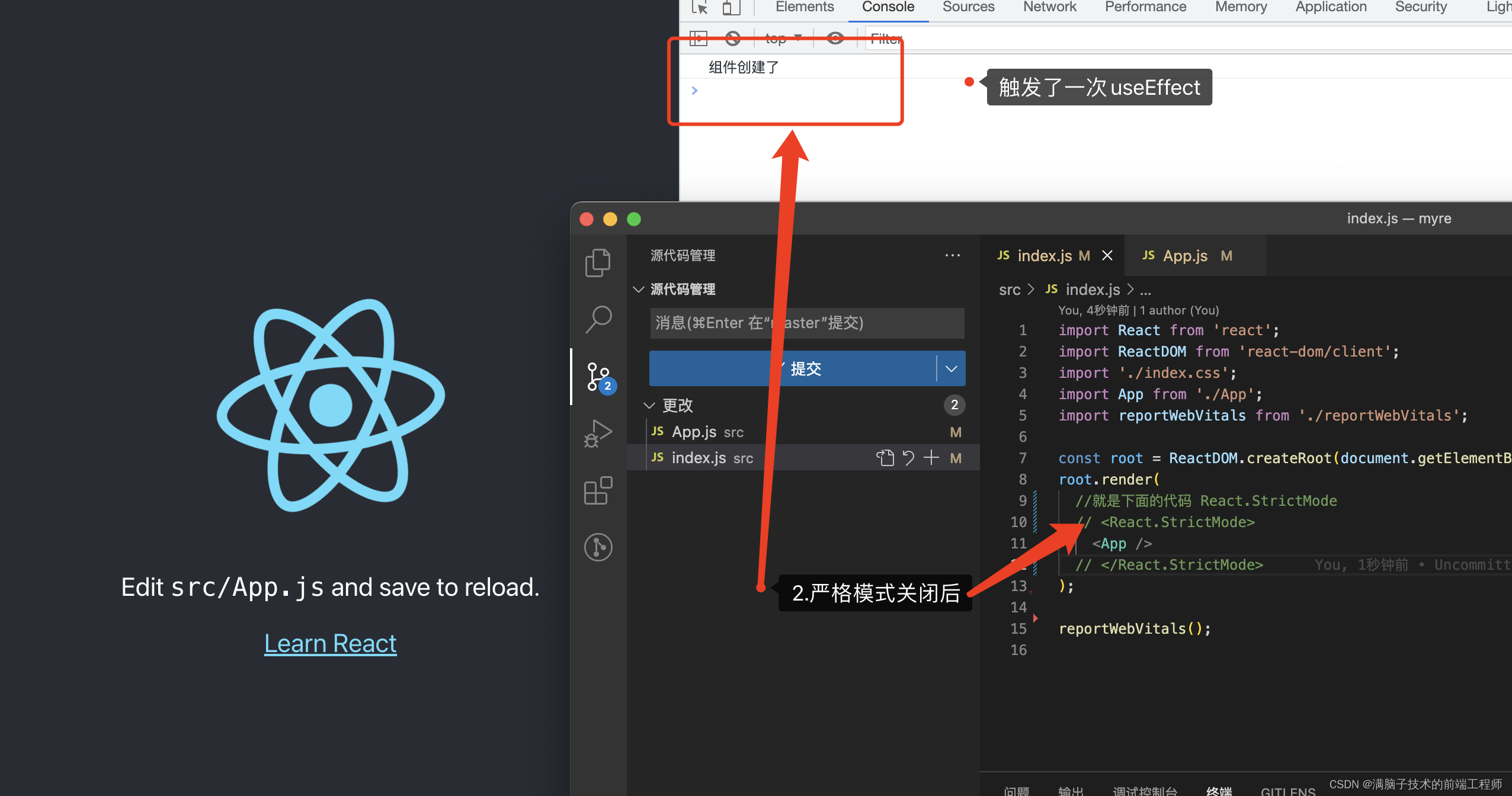
为什么要使用稀疏数组而不是别的数据结构?为什么它能实现对二维数组的压缩?
别急,一图以蔽之。
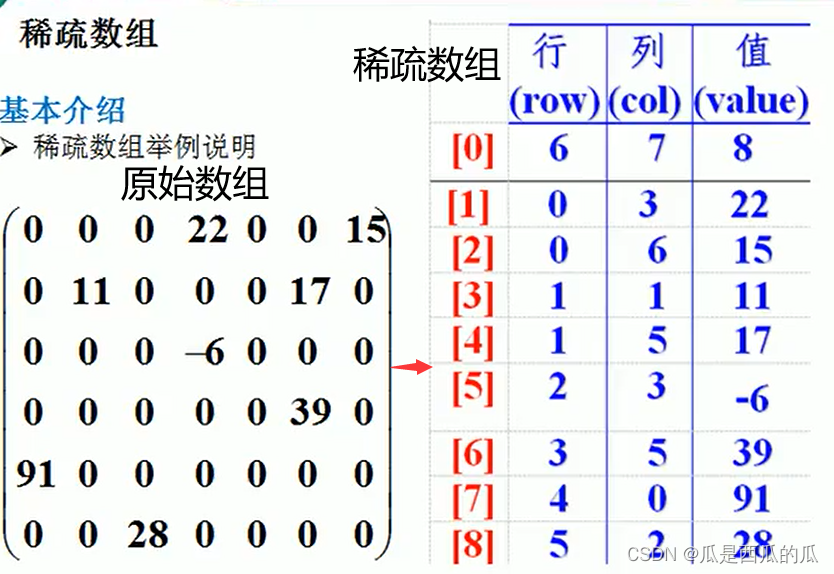
稀疏数组的处理方式:
1、分别记录原数组的行个数、列个数、有多少个“有效数据”。【第一行】
2、将不同有效数据的元素的行、列、值信息记录在一个小规模的数组中,从而缩小程序的规模。【其余行】
稀疏数组很简单,上面两点足以概括。
具体思路

二维数组转稀疏数组
1.遍历原始的二维数组,得到有效数据的个数 sum
2根据sum就可以创建稀疏数组 sparseArr int[sum+1][3]
注:此处之所以为[sum+1]的原因是第一列要存储原数组的大小及有效数的个数(sum)
3.将二维数组的有效数据数据存入到稀疏数组
稀疏数组转二维数组
1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的chessArr2= int[11][11]
⒉.在读取稀疏数组后几行的数据,并赋给原始的二维数组即可.
以上过程再配合Java的IO操作(写入磁盘文件,文件读入内存)就可以实现类似下棋游戏过程中的“存盘”,“读取” 的操作。
3.How?
二维数组转稀疏数组
//将二维数组压缩为稀疏数组
public static int[][] toSparseArray(int[][] arr){
//1.遍历二维数组,获取到二维数组中有效元素的个数
int sum = 0; //有效元素个数
//增强版双重for循环,实现遍历二维数组的操作
for (int[] ints : arr) {
for (int anInt : ints) {
if (anInt != 0) {
sum++;
}
}
}
//2.根据sum的个数及稀疏数组的设定来建立一个原数组所对应的稀疏数组
int[][] sparseArray = new int[sum+1][3];
//3.根据原数组的情况为稀疏数组赋值
//3.1第一行存储原二维数组的信息,首先填写它的数据
sparseArray[0][0] = arr.length; //原二维数组行长度
sparseArray[0][1] = arr[0].length; //原二维数组列长度
sparseArray[0][2] = sum; //有效数的个数
//3.2其余行存储有效数在原二维数组中的行、列及数值
int index = 0;
for(int i=0; i<arr.length; i++){
for (int j=0; j<arr[0].length; j++){
if (arr[i][j] != 0){
index++;
sparseArray[index][0] = i;
sparseArray[index][1] = j;
sparseArray[index][2] = arr[i][j];
}
}
}
return sparseArray;
}
稀疏数组还原为二维数组
//将稀疏数组转换为原二维数组
public static int[][] toErWei(int[][] arr){
//1.新建一个二维数组,读取稀疏数组的第一行,根据第一行数据初始化二维数组
int[][] erWei = new int[arr[0][0]][arr[0][1]]; //此时二维数组大小确定,内容全是0
//2,读取稀疏数组后几行数据,并赋给初始化好的二维数组
for (int i=1;i<arr.length;i++){ //i=1表示从稀疏数组的第二行开始读取
//0存储行信息,1存储列信息,2存储值信息
erWei[arr[i][0]][arr[i][1]]=arr[i][2]; //认真理解
}
return erWei;
}
源码
public class sparseArray {
public static void main(String[] args) {
int[][] erWei = new int[11][11];
for (int i=0; i<erWei.length-1; i++){
for (int j=0; j<erWei[0].length-1; j++){
erWei[i][j] = 0;
}
}
//设定有效元素
erWei[2][5] = 16;
erWei[1][6] = 14;
erWei[7][9] = 28;
erWei[4][5] = 20;
erWei[1][3] = 17;
erWei[6][4] = 79;
//输出原二维数组
printArr(erWei);
//转化为稀疏数组
int[][] sparseArray = toSparseArray(erWei);
printArr(sparseArray);
//转化为二维数组
int[][] ErWei = toErWei(sparseArray);
printArr(ErWei);
}
//将二维数组压缩为稀疏数组
public static int[][] toSparseArray(int[][] arr){
//1.遍历二维数组,获取到二维数组中有效元素的个数
int sum = 0; //有效元素个数
//增强版双重for循环,实现遍历二维数组的操作
for (int[] ints : arr) {
for (int anInt : ints) {
if (anInt != 0) {
sum++;
}
}
}
//2.根据sum的个数及稀疏数组的设定来建立一个原数组所对应的稀疏数组
int[][] sparseArray = new int[sum+1][3];
//3.根据原数组的情况为稀疏数组赋值
//3.1第一行存储原二维数组的信息,首先填写它的数据
sparseArray[0][0] = arr.length; //原二维数组行长度
sparseArray[0][1] = arr[0].length; //原二维数组列长度
sparseArray[0][2] = sum; //有效数的个数
//3.2其余行存储有效数在原二维数组中的行、列及数值
int index = 0;
for(int i=0; i<arr.length; i++){
for (int j=0; j<arr[0].length; j++){
if (arr[i][j] != 0){
index++;
sparseArray[index][0] = i;
sparseArray[index][1] = j;
sparseArray[index][2] = arr[i][j];
}
}
}
return sparseArray;
}
//将稀疏数组转换为原二维数组
public static int[][] toErWei(int[][] arr){
//1.新建一个二维数组,读取稀疏数组的第一行,根据第一行数据初始化二维数组
int[][] erWei = new int[arr[0][0]][arr[0][1]]; //此时二维数组大小确定,内容全是0
//2,读取稀疏数组后几行数据,并赋给初始化好的二维数组
for (int i=1;i<arr.length;i++){ //i=1表示从稀疏数组的第二行开始读取
//0存储行信息,1存储列信息,2存储值信息
erWei[arr[i][0]][arr[i][1]]=arr[i][2]; //认真理解
}
return erWei;
}
//输出数组信息
public static void printArr(int[][] arr){
for (int[] ints : arr){
for (int anInt : ints) {
System.out.print(anInt + " ");
}
System.out.println();
}
System.out.println("---------------------");
}
}
运行结果如下:
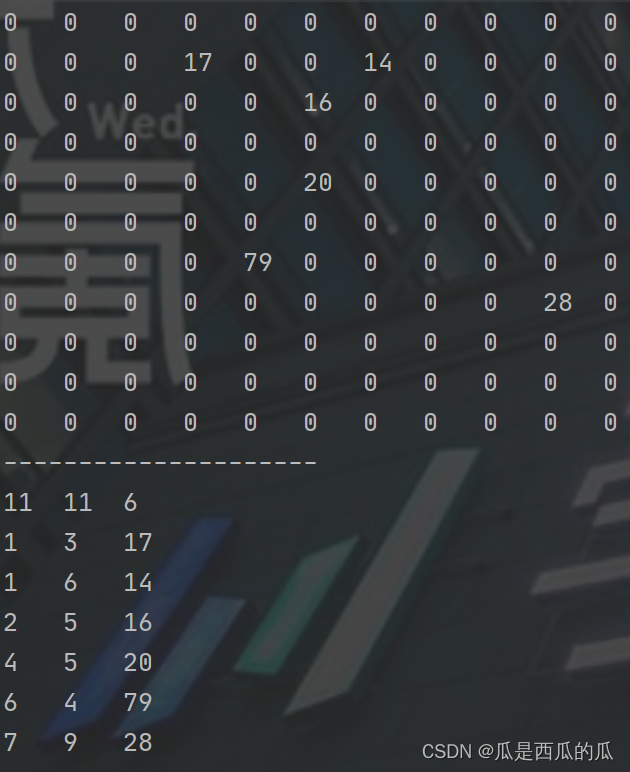
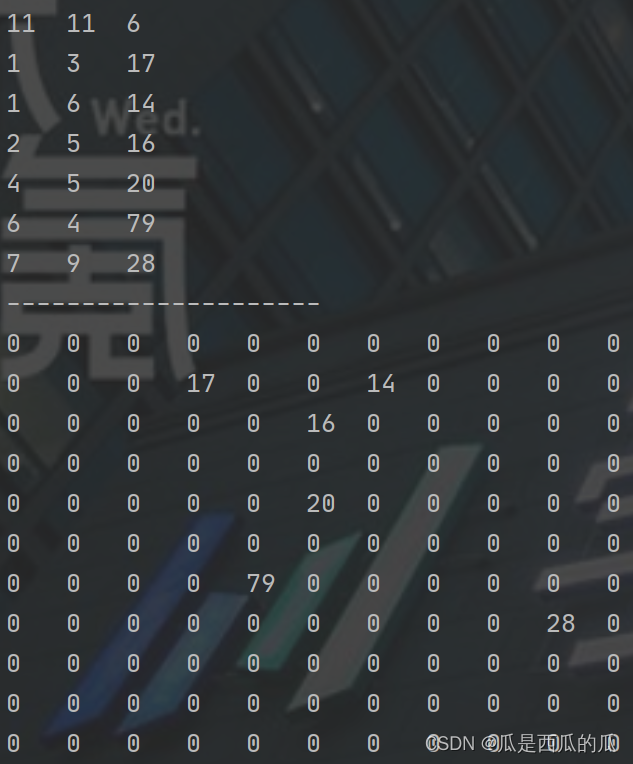
如上图所示,二维数组压缩为稀疏数组确实极大地节省了存储空间。同样可以通过稀疏数组在读盘时将其进行复原,达到预期需求。