【高性能计算】TVM使用TE手动优化矩阵乘法算法解析与代码解读

news2025/1/25 9:03:36

引言

注：本文主要介绍、解释TVM的矩阵优化思想、代码，需要配合代码注释一起阅读。

矩阵乘法是计算密集型运算。为了获得良好的 CPU 性能，有两个重要的优化措施：

  • 提高内存访问的高速缓存命中率。复杂的数值计算和热点内存（hot-spot memory）访问都可以通过高缓存命中率（high cache hit rate）来加速。这就要求我们将原内存（origin ）访问模式转化为符合高速缓存策略的模式。

  • SIMD（单指令多数据），也被称为矢量处理单元。在每个周期中，SIMD 可以处理一小批数据，而不是处理一个单一的值。这就要求我们将循环体中的数据访问模式转化为统一模式，以便编译器后端可以将其降低到 SIMD。

1- 基于TVM和Numpy的基线实现

这是numpy 实现矩阵乘法的实现代码，作为实现比较的基础benchmark，他的速度并不会很慢，这是因为其本身就采用了加速矩阵数学计算的算法实现。

import tvm
import tvm.testing
from tvm import te
import numpy

# The size of the matrix
# (M, K) x (K, N)
# You are free to try out different shapes, sometimes TVM optimization outperforms numpy with MKL.
M = 1024
K = 1024
N = 1024

# The default tensor data type in tvm
dtype = "float32"

# You will want to adjust the target to match any CPU vector extensions you
# might have. For example, if you're using using Intel AVX2 (Advanced Vector
# Extensions) ISA for SIMD, you can get the best performance by changing the
# following line to ``llvm -mcpu=core-avx2``, or specific type of CPU you use.
# Recall that you're using llvm, you can get this information from the command
# ``llc --version`` to get the CPU type, and you can check ``/proc/cpuinfo``
# for additional extensions that your processor might support.

target = tvm.target.Target(target="llvm", host="llvm")
dev = tvm.device(target.kind.name, 0)

# Random generated tensor for testing
a = tvm.nd.array(numpy.random.rand(M, K).astype(dtype), dev)
b = tvm.nd.array(numpy.random.rand(K, N).astype(dtype), dev)

# Repeatedly perform a matrix multiplication to get a performance baseline
# for the default numpy implementation
np_repeat = 100
np_running_time = timeit.timeit(  // 统计numpy.dot(a, b)计算耗时
    setup="import numpy\n"
    "M = " + str(M) + "\n"
    "K = " + str(K) + "\n"
    "N = " + str(N) + "\n"
    'dtype = "float32"\n'
    "a = numpy.random.rand(M, K).astype(dtype)\n"
    "b = numpy.random.rand(K, N).astype(dtype)\n",
    stmt="answer = numpy.dot(a, b)",
    number=np_repeat,
)
print("Numpy running time: %f" % (np_running_time / np_repeat))

answer = numpy.dot(a.numpy(), b.numpy())

现在用 TVM TE 编写基本的矩阵乘法，并验证它产生的结果与 numpy 的实现相同。我们还写了一个函数，它将帮助衡量调度优化的性能。

# TVM Matrix Multiplication using TE
k = te.reduce_axis((0, K), "k")  // 可以理解为约分轴，M*K * K*N = M*N，K轴维度消失啦
A = te.placeholder((M, K), name="A")  // 一种tensor，通常用于计算图的Input节点使用，没有前序节点
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda x, y: te.sum(A[x, k] * B[k, y], axis=k), name="C")  // 定义输出结果。第一个参数(M, N)表示输出矩阵的shape，lambda i:则可以理解为 for i: 0->n-1

# Default schedule
s = te.create_schedule(C.op)  // 从一个或多个 Tensor 的 Operation 进行创建
func = tvm.build(s, [A, B, C], target=target, name="mmult")

c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)


def evaluate_operation(s, vars, target, name, optimization, log):
    func = tvm.build(s, [A, B, C], target=target, name="mmult")
    assert func

    c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)
    func(a, b, c)
    tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)

    evaluator = func.time_evaluator(func.entry_name, dev, number=10)
    mean_time = evaluator(a, b, c).mean
    print("%s: %f" % (optimization, mean_time))
    log.append((optimization, mean_time))


log = []

evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="none", log=log)

让我们来看看上述使用 TVM 低级函数的运算器和默认调度的中间表示。请注意这个实现基本上是矩阵乘法的原始实现，在 A 和 B 矩阵的索引上使用三个嵌套循环。

先来看看原始的矩阵乘法实现，他基本没有考虑cache连续的问题：

for(int x = 0; x < M; x++){
	for(int y = 0; y < N; y++){
		for(int k = 0; k < K; k++){
			C[x][y] += A[x][k] * B[k][y];
		}
	}
}

TVM的计算其实是将二维矩阵平铺为了一维数组进行计算，由于边界定义为了1024，这里的offset也是1024

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  for (x: int32, 0, 1024) {  // 主要看这里，对应关系为 x->M y->N k->K
    for (y: int32, 0, 1024) {
      C[((x*1024) + y)] = 0f32
      for (k: int32, 0, 1024) {
        let cse_var_2: int32 = (x*1024)
        let cse_var_1: int32 = (cse_var_2 + y)
        C[cse_var_1] = (C[cse_var_1] + (A[(cse_var_2 + k)]*B[((k*1024) + y)]))
      }
    }
  }
}

2-使用TVM调度原语tile分块优化cache阻塞

提高缓冲区命中率的一个重要技巧是阻塞，在这个过程中，你的内存访问结构是在一个块的内部有一个小的邻域，具有很高的内存定位性。在本教程中，我们选择一个 32 的块因子。这将导致一个块充满 32 * 32 * sizeof(float) 的内存区域。这相当于一个 4KB 的缓存大小，而 L1 缓存的参考缓存大小为 32KB。

对矩阵计算进行分块，以加速。分块可以进一步的提升B、C矩阵的空间局部性， 我们把C分成多个title，然后针对每一个title，A和B中对应的行tile和列tile也会切成相应大小的tile进行多个小矩阵乘法，最后加和到C的tile中，当我们把tile的大小限定到合适的范围内时，就可以把整个tile填充到cache内，分块的好处就体现在一个block内的计算小到可以被cache容纳，以充分利用cache快速的读写速度。

我们首先为 C 矩阵计算操作创建一个默认的调度，然后用指定的块因子对其应用一个 tile 调度原语，调度原语返回所产生的循环顺序，从最外层到最内层，作为一个向量 [x_outer, y_outer, x_inner, y_inner]。然后我们得到操作输出的还原轴，并使用 4 的因子对其进行分割操作。这个因子并不直接影响我们现在正在进行的阻塞优化，但在以后我们应用矢量化时将会很有用。

现在操作已经被阻塞了，我们可以重新调度计算的顺序，把较少操作放到计算的最外层循环中，帮助保证被阻止的数据仍然在缓存中。这样就完成了调度，我们可以建立并测试与原生的调度相比的性能。

bn = 32

# Blocking by loop tiling
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)  // 分割

# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)

evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="blocking", log=log)

通过重新安排计算顺序以利用缓存，你应该看到计算的性能有了明显的改善。现在，打印内部表示，并将其与原始表示进行比较。

print(tvm.lower(s, [A, B, C], simple_mode=True))

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  for (x.outer: int32, 0, 32) {  // 外部32个分块
    for (y.outer: int32, 0, 32) {
      for (x.inner.init: int32, 0, 32) {  // 内部32*32个浮点数
        for (y.inner.init: int32, 0, 32) {
          C[((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)) + y.inner.init)] = 0f32  // 32768为32*32*32，初始化该块内的数为0
        }
      }
      for (k.outer: int32, 0, 256) {  // k轴分为4份，1024/4=256
        for (k.inner: int32, 0, 4) {  // 这里的4主要用于后面的SIMD的使用
          for (x.inner: int32, 0, 32) {
            for (y.inner: int32, 0, 32) {
              let cse_var_3: int32 = (y.outer*32)
              let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
              let cse_var_1: int32 = ((cse_var_2 + cse_var_3) + y.inner)
              C[cse_var_1] = (C[cse_var_1] + (A[((cse_var_2 + (k.outer*4)) + k.inner)]*B[((((k.outer*4096) + (k.inner*1024)) + cse_var_3) + y.inner)])) 
               // 其实这里B依然是cache不友好读取，即跳行读取，但可能是考虑到在一个定义的分块cache内
            }
          }
        }
      }
    }
  }
}

3-利用SIMD矢量化计算

另一个重要的优化技巧是矢量化。当内存访问模式是统一的，编译器可以检测到这种模式并将连续的内存传递给 SIMD 矢量处理器。在 TVM 中，我们可以使用 vectorize 接口来提示编译器这种模式，利用这一硬件特性。

  • SIMD 的全称是 Single Instruction Multiple Data，中文名“单指令多数据”。顾名思义，一条指令处理多个数据。

在本教程中，我们选择对内循环的行数据进行矢量化，因为在我们之前的优化中，它已经是缓存友好的。

# Apply the vectorization optimization
s[C].vectorize(yi)  // 对子块内的每一行进行SIMD计算

evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="vectorization", log=log)

# The generalized IR after vectorization
print(tvm.lower(s, [A, B, C], simple_mode=True))

vectorization: 0.257297
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  for (x.outer: int32, 0, 32) {
    for (y.outer: int32, 0, 32) {
      for (x.inner.init: int32, 0, 32) {
        C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
      }
      for (k.outer: int32, 0, 256) {
        for (k.inner: int32, 0, 4) {
          for (x.inner: int32, 0, 32) {  // 对于y.inner的每一行，使用128位SIMD计算，32*4，一次计算4位
            let cse_var_3: int32 = (y.outer*32)
            let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
            let cse_var_1: int32 = (cse_var_2 + cse_var_3)
            C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_2 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3), 1, 32)]))
          }
        }
      }
    }
  }
}

4-使用循环优化

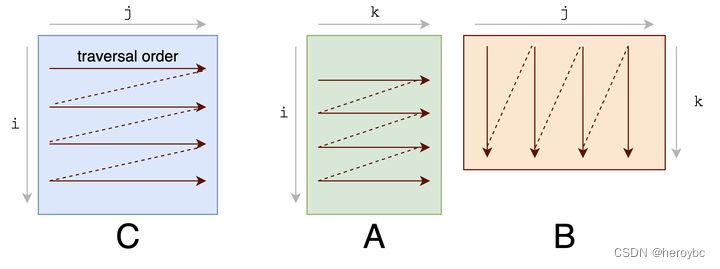
如果我们看一下上面的 IR，我们可以看到内循环的行数据被矢量化，B 被转化为 分块B（这从内循环的 (float32x32*)B2 部分可以看出）。现在 B的分块 的遍历是顺序的。所以我们要看一下 A 的访问模式。在当前的计划中，A 是被逐列访问的，每次访问A的128位，这对缓冲区不友好。如果我们改变 ki 和内轴 xi 的嵌套循环顺序，A 矩阵的访问模式将对缓存更友好。
在这里插入图片描述

s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)

# re-ordering
s[C].reorder(xo, yo, ko, xi, ki, yi)  // 改变循环顺序
s[C].vectorize(yi)

evaluate_operation(
    s, [A, B, C], target=target, name="mmult", optimization="loop permutation", log=log
)

# Again, print the new generalized IR
print(tvm.lower(s, [A, B, C], simple_mode=True))

loop permutation: 0.130006
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  for (x.outer: int32, 0, 32) {
    for (y.outer: int32, 0, 32) {
      for (x.inner.init: int32, 0, 32) {
        C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
      }
      for (k.outer: int32, 0, 256) {
        for (x.inner: int32, 0, 32) {
          for (k.inner: int32, 0, 4) {  // 调换了这里的顺序
            let cse_var_3: int32 = (y.outer*32)
            let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
            let cse_var_1: int32 = (cse_var_2 + cse_var_3)
            C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_2 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3), 1, 32)]))
          }
        }
      }
    }
  }
}

5-使用数组打包

另一个重要的技巧是数组打包。这个技巧是对数组的存储维度进行重新排序，将某些维度上的连续访问模式转换为扁平化后的顺序模式。

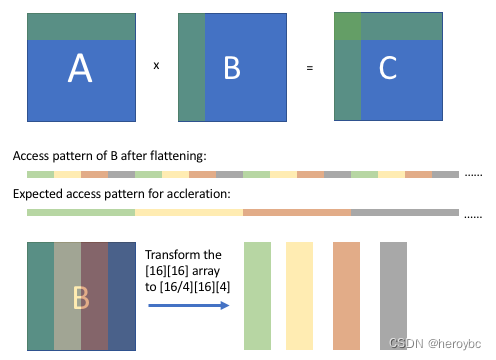
在这里插入图片描述

正如上图所示，在阻塞计算后，我们可以观察到 B 的数组访问模式（扁平化后），它是有规律的，但是不连续的。我们期望经过一些转换后，我们可以得到一个连续的访问模式。通过将 [16][16] 数组重新排序为 [16/4][16][4] 数组，当从打包的数组中抓取相应的值时，B 的访问模式将是连续的。

为了实现这一目标，将不得不从新的默认调度开始，考虑到 B 的新包装，值得花点时间来评论一下。TE 是编写优化运算符的强大而富有表现力的语言，但它往往需要对你所编写的底层算法、数据结构和硬件目标有一些了解。在本教程的后面，我们将讨论一些让 TVM 承担这一负担的选项。无论如何，让我们继续编写新的优化调度。

这里的本质相当于改变了B的按列读取，改为按行读取，即cache友好。

// 必须重写算法。对计算方式进行重新定义。
packedB = te.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name="packedB")
C = te.compute(
    (M, N),
    lambda x, y: te.sum(A[x, k] * packedB[y // bn, k, tvm.tir.indexmod(y, bn)], axis=k),  // TIR 的全称是 Tensor IR, tvm.tir.indexmod 为计算y/bn的余数
    name="C",
)

s = te.create_schedule(C.op)

xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)

s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)

x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)  // 执行向量操作的指令。vectorize 是并发思路在CPU里的最细粒度实现。
s[packedB].parallel(x)

evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="array packing", log=log)

# Here is the generated IR after array packing.
print(tvm.lower(s, [A, B, C], simple_mode=True))

array packing: 0.140257
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {
    for (x: int32, 0, 32) "parallel" {
      for (y: int32, 0, 1024) {
        packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
      }
    }
    for (x.outer: int32, 0, 32) {
      for (y.outer: int32, 0, 32) {
        for (x.inner.init: int32, 0, 32) {
          C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
        }
        for (k.outer: int32, 0, 256) {
          for (x.inner: int32, 0, 32) {
            for (k.inner: int32, 0, 4) {
              let cse_var_3: int32 = ((x.outer*32768) + (x.inner*1024))
              let cse_var_2: int32 = (k.outer*4)
              let cse_var_1: int32 = (cse_var_3 + (y.outer*32))
              C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_3 + cse_var_2) + k.inner)], 32)*packedB_1[(((y.outer*1024) + cse_var_2) + k.inner)]))
            }
          }
        }
      }
    }
  }
}

6-通过缓存优化块的写入

到目前为止，我们所有的优化都集中在有效地访问和计算 A 和 B 矩阵的数据以计算 C 矩阵上。在阻塞优化之后，运算器将逐块地将结果写入 C，而且访问模式不是顺序的。我们可以通过使用一个顺序缓存数组来解决这个问题，使用 cache_write、compute_at 和 unroll 的组合来保存块结果，并在所有块结果准备好后写入 C。

cache_write和cache_read对应，是先在shared memory中存放计算结果，最后将结果写回到global memory。当然在真实的场景中，我们往往是会将结果先放着register中，最后写回。

s = te.create_schedule(C.op)

# Allocate write cache
CC = s.cache_write(C, "global")

xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)

# Write cache is computed at yo
s[CC].compute_at(s[C], yo)  // 默认情况下，TVM将在函数的最外层或根计算张量。compute_at指定应在另一个运算符的第一个计算轴上计算一个张量。应该是为了方便后续的在xo维度上进行并行计算。

# New inner axes
xc, yc = s[CC].op.axis

(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)  // 循环展开
s[CC].vectorize(yc)

x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)

evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="block caching", log=log)

# Here is the generated IR after write cache blocking.
print(tvm.lower(s, [A, B, C], simple_mode=True))

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global;
  allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global {
    for (x: int32, 0, 32) "parallel" {
      for (y: int32, 0, 1024) {
        packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
      }
    }
    for (x.outer: int32, 0, 32) {
      for (y.outer: int32, 0, 32) {
        for (x.c.init: int32, 0, 32) {
          C.global_1: Buffer(C.global, float32, [1024], [])[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)
        }
        for (k.outer: int32, 0, 256) {
          for (x.c: int32, 0, 32) {
            let cse_var_4: int32 = (k.outer*4)
            let cse_var_3: int32 = (x.c*32)
            let cse_var_2: int32 = ((y.outer*1024) + cse_var_4)
            let cse_var_1: int32 = (((x.outer*32768) + (x.c*1024)) + cse_var_4)
             {
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[cse_var_1], 32)*packedB_1[cse_var_2]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 1)], 32)*packedB_1[(cse_var_2 + 1)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 2)], 32)*packedB_1[(cse_var_2 + 2)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 3)], 32)*packedB_1[(cse_var_2 + 3)]))
            }
          }
        }
        for (x.inner: int32, 0, 32) {
          for (y.inner: int32, 0, 32) {
            C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global_1[((x.inner*32) + y.inner)]
          }
        }
      }
    }
  }
}

7-并行化

到目前为止，我们的计算只被设计为使用单核。几乎所有的现代处理器都有多个内核，计算可以从并行运行的计算中获益。最后的优化是利用线程级并行化的优势。

# parallel
s[C].parallel(xo)

x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)

evaluate_operation(
    s, [A, B, C], target=target, name="mmult", optimization="parallelization", log=log
)

# Here is the generated IR after parallelization.
print(tvm.lower(s, [A, B, C], simple_mode=True))

parallelization: 0.026403
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
  allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {
    for (x: int32, 0, 32) "parallel" {
      for (y: int32, 0, 1024) {
        packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
      }
    }
    for (x.outer: int32, 0, 32) "parallel" {
      allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global;
      for (y.outer: int32, 0, 32) {
        for (x.c.init: int32, 0, 32) {
          C.global_1: Buffer(C.global, float32, [1024], [])[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)
        }
        for (k.outer: int32, 0, 256) {
          for (x.c: int32, 0, 32) {
            let cse_var_4: int32 = (k.outer*4)
            let cse_var_3: int32 = (x.c*32)
            let cse_var_2: int32 = ((y.outer*1024) + cse_var_4)
            let cse_var_1: int32 = (((x.outer*32768) + (x.c*1024)) + cse_var_4)
             {
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[cse_var_1], 32)*packedB_1[cse_var_2]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 1)], 32)*packedB_1[(cse_var_2 + 1)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 2)], 32)*packedB_1[(cse_var_2 + 2)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 3)], 32)*packedB_1[(cse_var_2 + 3)]))
            }
          }
        }
        for (x.inner: int32, 0, 32) {
          for (y.inner: int32, 0, 32) {
            C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global_1[((x.inner*32) + y.inner)]
          }
        }
      }
    }
  }
}

总结

如前所述，如何使用 TE 和调度原语进行优化，可能需要对底层架构和算法有一些了解。然而，TE 的设计是作为更复杂的算法的基础，可以搜索潜在的优化。

本教程提供了一个 TVM 张量表达（TE）工作流程的演练，使用了一个矢量添加和一个矩阵乘法的例子。一般的工作流程是：

  • 通过一系列的操作来描述你的计算。
  • 描述我们要如何计算使用调度原语。
  • 编译到我们想要的目标函数。
  • 可以选择保存该函数以便以后加载。

参考资料

  • TVM官方教程：https://daobook.github.io/tvm/docs/tutorial/tensor_expr_get_started.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/376880.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

「TCG 规范解读」TCG 主规范-设计原则

「TCG 规范解读」TCG 主规范-设计原则

可信计算组织（Ttrusted Computing Group,TCG）是一个非盈利的工业标准组织，它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立，并采纳了由可信计算平台联盟（the Trusted Computing Platform Alliance,TCPA）所开发的规范。现在的规范都不是最终稿，都…
阅读更多...
【Python】元组如何创建？

【Python】元组如何创建？

嗨害大家好鸭&#xff01;我是小熊猫~ Python 元组 Python 的元组与列表类似&#xff0c; 不同之处在于元组的元素不能修改。 元组使用小括号&#xff0c;列表使用方括号。 元组创建很简单&#xff0c;只需要在括号中添加元素&#xff0c; 并使用逗号隔开即可。 如下实例…
阅读更多...
【线性筛】ccpc黑龙江省赛 F

【线性筛】ccpc黑龙江省赛 F

第一次vp省赛&#xff0c;只出了三题&#xff0c;很寄啊Problem - F - Codeforces题意&#xff1a;思路&#xff1a;题目一直在强调最小质因子&#xff0c;我们考虑边跑线性筛边求贡献一、对于第一种情况&#xff0c;即遇到的数是质数&#xff0c;贡献直接1就好了二、对于第二种…
阅读更多...
mac在命令行里获取root权限

mac在命令行里获取root权限

1、为什么要获取root权限&#xff1f; 答&#xff1a;一些命令在正常状态下没有权限会报错&#xff0c;只有获取了root权限才能正常操作。 比如我们想修改一些系统的文件&#xff1a; vim /etc/shells 1 修改后保存&#xff0c;发现没权限&#xff0c;报错了。如下图&#xf…
阅读更多...
MaxWell原理概述

MaxWell原理概述

文章目录1.MaxWell概述2.Maxwell输出数据格式3.Maxwell原理3.1 MySQL二进制日志3.2 MySQL主从复制1.MaxWell概述 Maxwell 是由美国Zendesk公司开源&#xff0c;用Java编写的MySQL变更数据抓取软件。它会实时监控Mysql数据库的数据变更操作&#xff08;包括insert、update、dele…
阅读更多...
传输层重点协议

传输层重点协议

1.TCP协议 TCP&#xff0c;即Transmission Control Protocol&#xff0c;传输控制协议。人如其名&#xff0c;要对数据的传输进行一个详细的控制。 TCP协议段格式 源/目的端口号&#xff1a;表示数据是从哪个进程来&#xff0c;到哪个进程去&#xff1b;32位序号/32位确认号…
阅读更多...
第三章-OpenCV基础-6-滤波处理

第三章-OpenCV基础-6-滤波处理

前置内容 在尽量保留图片原有信息的情况下,过滤掉图像内部的噪声的过程成为对图像的平滑处理(又称滤波处理),所得到的图像成为平滑图像(把图像中的噪点过滤掉,生成一个相对平滑的图像)。 举个栗子: 一个图像有个噪点,加载发现有个点的像素值和周边像素值差异太大格格不入,使用…
阅读更多...
[C++]多态

[C++]多态

&#x1f941;作者&#xff1a; 华丞臧 &#x1f4d5;​​​​专栏&#xff1a;【C】 各位读者老爷如果觉得博主写的不错&#xff0c;请诸位多多支持(点赞收藏关注)。如果有错误的地方&#xff0c;欢迎在评论区指出。 推荐一款刷题网站 &#x1f449;LeetCode 文章目录一、多态…
阅读更多...
【Opencv项目实战】背景替换：帮你的证件照换个背景色

【Opencv项目实战】背景替换：帮你的证件照换个背景色

文章目录方法一、基于removebg的背景替换1.1、removebg介绍1.2、环境配置1.3、算法详解1.4、实战&#xff1a;单张图片背景替换1.5、实战&#xff1a;多张图片背景替换1.6、实战&#xff1a;UI自选择图片进行背景替换方法二、基于backgroundremover的背景替换2.1、backgroundre…
阅读更多...
创建对象的方式和对属性的操作

创建对象的方式和对属性的操作

javaScript支持多种编程范式&#xff0c;包括函数式编程和面向对象编程&#xff0c;javaScript的对象被设计成一组属性的无序集合&#xff0c;由key和value组成。 创建对象的两种方式 早期使用创建对象方式最多的是使用Object类&#xff0c;使用new关键字来创建一个对象&…
阅读更多...
应用篇|网络安全知识培训考试，答题小程序操作指引

应用篇|网络安全知识培训考试，答题小程序操作指引

网络安全知识培训考试&#xff0c;答题小程序操作指引关于全民防诈反诈宣传或者网络安全知识学习&#xff0c;如何进行组织一场微信线上答题考试&#xff1f;可以在小程序“护网专题信息安全知识竞答”&#xff0c;先创建一个学习单位/小组&#xff0c;再邀请成员加入单位/小组…
阅读更多...
如何构造个人 AI 策略：从 AI 绘画的演进与 ChatGPT 现状出发？

如何构造个人 AI 策略：从 AI 绘画的演进与 ChatGPT 现状出发？

持续关注 AI 相关探索&#xff1a;https://github.com/phodal/ai-researchPS&#xff1a;就本文的结论而言&#xff0c;我相信你已经或多或少的有所体会了。也因此&#xff0c;本文更多的是展现一个思考的过程&#xff0c;而不是一个纯粹的结论。AIGC 是什么&#xff1f;它是指…
阅读更多...
pyenv安装python虚拟环境

pyenv安装python虚拟环境

文章目录pyenv介绍准备工作安装pyenv设置虚拟环境pyenv介绍 pyenv是一个forked自ruby社区的简单、低调、遵循UNIX哲学的Python环境管理工具, 它可以轻松切换全局解释器版本, 同时结合vitualenv插件可以方便的管理对应的包源。 为什么我们需要pyenv呢 Python解释器版本混乱, 2…
阅读更多...
怎么关闭win10自动更新？我们可以这么做！

怎么关闭win10自动更新？我们可以这么做！

Win10自动更新可以使系统保持最新状态&#xff0c;但也可能导致一些问题&#xff0c;例如占用大量网络流量&#xff0c;导致系统速度减慢等。如果你希望关闭win10自动更新&#xff0c;不要电脑自动更新&#xff0c;我们可以跟着这篇文章这么做&#xff01; 操作环境&#xff1a…
阅读更多...
测试行业干了5年，从只会点点点到了现在的测试开发，总算是证明了自己

测试行业干了5年，从只会点点点到了现在的测试开发，总算是证明了自己

测试不止是点点点 我感觉我是一个比较有发言权的人吧&#xff0c;我在测试行业摸爬滚打5年&#xff0c;以前经常听到开发对我说&#xff0c;天天的点点点有意思没&#xff1f; 和IT圈外的同学、朋友聊起自己的工作&#xff0c;往往一说自己是测试&#xff0c;无形中也会被大家…
阅读更多...
Jmeter 连接 JDBC 报错Communications link failure解决办法（云服务器搭建了LNMP环境必看）

Jmeter 连接 JDBC 报错Communications link failure解决办法（云服务器搭建了LNMP环境必看）

换jar包、加?useSSLfalse&#xff0c;3306加防火墙&#xff0c;都不能解决我的问题。最终我发现是我的LNMP环境导致 错误提示 Response message:java.sql.SQLException: Cannot create PoolableConnectionFactory (Communications link failureThe last packet sent successf…
阅读更多...
【跨尺度学习：迭代残差：超分：泛锐化】

【跨尺度学习：迭代残差：超分：泛锐化】

Pansharpening via Super-Resolution Iterative Residual Network With a Cross-Scale Learning Strategy &#xff08;基于跨尺度学习策略的超分辨率迭代残差网络泛锐化&#xff09; 全色锐化是利用高空间分辨率全色&#xff08;HR PAN&#xff09;图像恢复低空间分辨率多光…
阅读更多...
Vue-Router 路由管理器

Vue-Router 路由管理器

文章目录知识点前端路由的概念及作用Vue-Router 的安装Vue-Router 的基本使用知识点 前端路由的概念及作用Vue-Router 的安装Vue-Router 的基本使用 前端路由的概念及作用 需要大家注意的是&#xff0c;这里的路由可不是指我们日常生活中的路由器 &#x1f602; &#xff0c;…
阅读更多...
Allegro如何打开或者关闭DFA规则设置操作指导

Allegro如何打开或者关闭DFA规则设置操作指导

Allegro如何打开或者关闭DFA规则设置操作指导 在用Allegro做PCB布局的时候，器件与器件之间的DFA规则可以避免器件出现装配问题。如下图 当DFA规则设置好之后，如何打开或者关闭规则，具体操作如下 点击Setup点击Constraints
阅读更多...
华为OD机试题，用 Java 解【相同数字的积木游戏 1】问题

华为OD机试题，用 Java 解【相同数字的积木游戏 1】问题

最近更新的博客 华为OD机试题，用 Java 解【停车场车辆统计】问题华为OD机试题，用 Java 解【字符串变换最小字符串】问题华为OD机试题，用 Java 解【计算最大乘积】问题华为OD机试题，用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数（Java） | 机试题算法思路 【2023】使…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023