文章目录
- 一、二叉树前序遍历
- 二、二叉树层序遍历
- 三、按照之字形打印二叉树
- 四、二叉树中和为某一值的路径(一)
- 五、二叉搜索树与双向链表
- 六、合并二叉树
- 七、二叉树的镜像
- 八、判断是否为二叉搜索树
- 九、判断是否为完全二叉树
- 十、判断是否为平衡二叉树
- 总结
提示:本人是正在努力进步的小菜鸟,不喜勿喷~,如有大佬发现某题有更妙的解法和思路欢迎提出讨论~
一、二叉树前序遍历
OJ链接
📌📌📌题目描述:

返回值: int[]
📌📌📌解题思路:
根据 “根左右” 的原则逐个遍历二叉树,并用 ArrayList 记录二叉树的每一个结点,递归结束后把 ArrayList 中记录的结点逐个放在数组中
⚠️⚠️⚠️注意:
1,如果二叉树为空,返回的数组为:“ [ ] ”,所以数组长度必须初始化为0
2,不能 在递归过程中每遇到一个非空结点就放入数组中,因为无法确定二叉树的结点个数,从而 不能 确定数组长度,并且数组 不能 动态的每添加一个元素就增大一个容量,但是数据结构中存在类似功能的集合类:ArrayList
3,把先序遍历数组这个方法独立出来,每遍历一个非空结点就在 ArrayList 中插入一个数据,递归结束后 ArrayList 得到的就是二叉树的先序遍历序列
4,最后创建和 ArrayList 长度相同的数组,遍历数组设置每个下标的值即可
代码实现:
public class PreorderTraversal {
public int[] preorderTraversal (TreeNode root) {
int[] array = new int[0];
ArrayList<Integer> arrayList = new ArrayList<>();
preorder(arrayList,root);
int len = arrayList.size();
if(len == 0) {
return array;
}
array = new int[len];
for(int i = 0; i < len; i++) {
array[i] = arrayList.get(i);
}
return array;
}
// 先序遍历并在 ArrayList 中添加数据
// public void preorder(ArrayList arrayList, TreeNode root) {
// 会发生警告:“ 参数化类“ArrayList”的原始使用 ” ——使用泛型类做参数要加上 “ <对应类型> ”
public void preorder(ArrayList<Integer> arrayList, TreeNode root) {
if(root == null) {
return;
}
arrayList.add(root.val);
preorder(arrayList,root.left);
preorder(arrayList,root.right);
}
}
二叉树的中序,后序遍历的思路和先序遍历一致,只需要改变递归过程中 以下三行代码的先后执行顺序即可
arrayList.add(root.val);
preorder(arrayList,root.left);
preorder(arrayList,root.right);
二、二叉树层序遍历
OJ链接
📌📌📌题目描述:

返回值: ArrayList<ArrayList<Integer>>
📌📌📌解题思路:
返回值是 ArrayList 集合类,并且要一层一层的记录,所以 ArrayList 的每一个元素也是一个 ArrayList ,如图:
有点类似于二维数组。重点在于如何在层序遍历的同时分层,可以分成两部分:层序遍历 + 分层。
层序遍历与之前先序遍历不同,层序遍历不使用递归,而是利用队列这种数据结构。如果能在访问(出队)根节点的同时,入队 这个根 的 左右子树的根节点,然后再做到这一层的根节点全部出队后,再依次出队下一层

如何把这个队列分层呢?

每一层的节点个数,就是队列出队的次数,所以定义一个 size,控制出队的循环次数即可
⚠️⚠️⚠️注意:
1,循环之前让根节点 root 入队,循环的大前提条件是队列不为空,如果队列为空说明所有的结点全部出队,退出循环返回 list
2,内部循环控制每一层的循环次数,也就是这一层的节点个数, 每层循环开始前 new 一个新的 ArrayList
3,Queue 的泛型类型必须是 TreeNode 而不能是 Integer ,如果是 Integer ,在每层的 ArrayList 中插入时看似可以直接、方便的插入 queue
4. ❓❓❓queue.poll()方法的返回值也是 TreeNode 类型,需用一个变量 node 接收才能访问到这个结点的 val 域,同时在判断左右孩子是否为空时,是 if (node.left != null),而不是 if (root.left != null),如果是后者,代码执行到此说明 root 不为空,而 if 语句每次都会进来,最后会访问空结点的左右孩子,发生空指针异常
代码实现:
public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
ArrayList<ArrayList<Integer>> list = new ArrayList<>();
if (root == null) {
return list;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
ArrayList<Integer> inList = new ArrayList<>();
while (size > 0) {
TreeNode node = queue.poll();
inList.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
size--;
}
list.add(inList);
}
return list;
}
三、按照之字形打印二叉树
OJ链接
📌📌📌题目描述:

返回值: ArrayList<ArrayList<Integer>>
📌📌📌解题思路:
通过题目描述得知,之字形打印就是在上一题层序遍历的输出结果上, 奇数行从左往右访问, 偶数行从右往左遍历,最简单的方式就是在上一题的代码上, 再写一个“反转”函数
代码实现:
public class PrintZ {
public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> list = new ArrayList<>();
if (pRoot == null) {
return list;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(pRoot);
int line = 0;
while (!queue.isEmpty()) {
int size = queue.size();
ArrayList<Integer> inList = new ArrayList<>();
while (size > 0) {
TreeNode node = queue.poll();
inList.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
// 如果偶数行就反转,把顺序改成逆序
if (node.right != null) {
queue.offer(node.right);
}
size--;
}
if((++line)%2 == 0) {
list.add(reverse(inList));
}else {
list.add(inList);
}
}
return list;
}
// 反转ArrayList
private ArrayList<Integer> reverse(ArrayList<Integer> arrayList) {
int size = arrayList.size();
ArrayList<Integer> ret = new ArrayList<>();
for (int i = 0; i < size; i++) {
ret.add(arrayList.get(size-i -1 ));
}
return ret;
}
}
四、二叉树中和为某一值的路径(一)
OJ链接
📌📌📌题目描述:

返回值: boolean
📌📌📌解题思路:
判断是否有一条路径(走到头时), 一路上的结点 val 值综合相当于 sum
利用遍历思想, 前序遍历, 递归时传递 sum, 每遇到一个结点就减去当前结点的 val 值, 如果当前结点的左右孩子节点都为 null 说明当前结点是某条路径的尽头
此时进行判断 sum 和 0 是否相同, 如果 sum 等于 0 , 说明这一路是对的, 返回true,否则返回false
但是!!
返回 fasle 之后 ,有可能去右子树继续判断呢, 所以如果这条路不满足, 要把当前结点的 val 值加回来, 再返回
⚠️⚠️⚠️注意:
一定是当前结点为叶子节点, 也就是某条路径的尽头时再判断 sum 和 0 的关系
代码实现:
public class HasPathSum{
public boolean hasPathSum (TreeNode root, int sum) {
if (root == null) {
return false;
}
sum -= root.val;
if (sum == 0 && (root.left == null && root.right == null)) {
return true;
}
if (sum != 0 && (root.left == null && root.right == null)) {
sum += root.val;
return false;
}
boolean bLeft = hasPathSum(root.left, sum);
boolean bRight = hasPathSum(root.right, sum);
return bLeft || bRight;
}
}
方法2: 也可以用加法, 多传递一个count, 从 0 往上加, 走到尽头时判断 count 是否和 sum 相同, 相同说明这条路径找到了, 返回true
代码实现:
public class HasPathSum2 {
public boolean hasPathSum (TreeNode root, int sum) {
int count = 0;
return hasPathSumChild(root,sum,count);
}
public boolean hasPathSumChild(TreeNode root, int sum, int count) {
if (root == null) {
return false;
}
count += root.val;
if (sum == count &&
(root.left == null && root.right == null)) {
return true;
}
if (sum != count &&
(root.left == null && root.right == null)) {
count -= root.val;
return false;
}
boolean leftIsTrue = hasPathSumChild(root.left, sum,count);
boolean rightIsTrue = hasPathSumChild(root.right, sum,count);
return leftIsTrue || rightIsTrue;
}
}
五、二叉搜索树与双向链表
OJ链接
📌📌📌题目描述:

返回值: TreeNode
📌📌📌解题思路:
首先分成两部分:树=》链表 + 寻找链表头结点
题目给定的是一个二叉搜索树, 二叉搜索树的性质是, 中序遍历时一定是有序的, 而题目要求正是把树转化成链表后的前驱后继符合二叉搜索树中序遍历的顺序
加之要在“原树”上操作, 所以本题基本思想就是对二叉搜索树进行中序遍历
问题在于, 如何更改每个结点的左右引用
既然是以左中右的顺序访问二叉搜索树, 当然是左遍历完,回到当前根节点的时候进行操作——更改引用, 我们需要定义一个 prevRoot 记录下来前一个结点, 让当前根节点 root 的 left 引用上一个结点,然后当 prevRoot 不为空时,让它的 right 引用当前根节点
⚠️⚠️⚠️注意:
prevRoot.right = root, 执行这条语句之前一定要对 prevRoot 判空, 避免空指针异常
代码实现:
public class TreeAndLinkedList {
// 把二叉搜索树更改为有序双向链表并返回链表头结点
public TreeNode prevRoot;
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree == null) {
return null;
}
// 通过中序遍历,从树转化成双向链表
inOrder(pRootOfTree);
return findHead(prevRoot);
}
private void inOrder(TreeNode root) {
if(root == null) {
return ;
}
inOrder(root.left);
// 修改left指向
root.left = prevRoot;
// 修改right指向
if(prevRoot != null) {
prevRoot.right = root;
}
prevRoot = root;
inOrder(root.right);
}
private TreeNode findHead(TreeNode root) {
while(root.left != null) {
root = root.left;
}
return root;
}
}
六、合并二叉树
OJ链接
📌📌📌题目描述:
已知两颗二叉树,将它们合并成一颗二叉树。合并规则是:都存在的结点,就将结点值加起来,否则空的位置就由另一个树的结点来代替。例如:
两颗二叉树是:


返回值 : TreeNode
📌📌📌解题思路:
典型的子问题思路, 对两棵树的相同位置上每一个结点判断即可
⚠️⚠️⚠️注意:
需要注意的是, 每次对两个结点判断操做后, 返回的是合并之后树的根节点, 可以让 t2 往 t1 上合并,最后返回 t1 的根结点, 也可以让 t1 往 t2 上合并, 最后返回 t2 的根节点
如果 t2 往 t1 上合并, 那么在左右递归时, 就需要接收返回值, 使当前根节点引用左右子树
代码实现:
public class MergeTree {
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
if(t1 == null && t2 == null){
return null;
}
if(t1 == null && t2 != null) {
return t2;
}
if(t1 != null && t2 != null ){
t1.val += t2.val;
}
if(t1 == null || t2 == null) {
return t1;
}
t1.left = mergeTrees(t1.left, t2.left);
t1.right = mergeTrees(t1.right,t2.right);
return t1;
}
}
七、二叉树的镜像
OJ链接
📌📌📌题目描述:

返回值: TreeNode
📌📌📌解题思路:
典型的子问题思路, 交换每一棵(子)树的左右子树即可
代码实现:
public class Mirror {
public TreeNode Mirror (TreeNode pRoot) {
if(pRoot == null) {
return null;
}
TreeNode tmp = pRoot.right;
pRoot.right = pRoot.left;
pRoot.left = tmp;
Mirror(pRoot.left);
Mirror(pRoot.right);
return pRoot;
}
}
八、判断是否为二叉搜索树
OJ链接
📌📌📌题目描述:

返回值 : boolean
📌📌📌解题思路:
利用搜索二叉树的特质, 对这棵树进行中序遍历, 存储中序遍历序列, 判断该序列是否有序, 如果满足有序说明是搜索二叉树, 否则不是
代码实现:
public class IsValidBST {
public boolean isValidBST (TreeNode root) {
ArrayList<Integer> list = new ArrayList<>();
inorder(list, root);
return jude(list);
}
private void inorder(ArrayList<Integer> list, TreeNode root) {
if(root == null) {
return;
}
inorder(list, root.left);
list.add(root.val);
inorder(list, root.right);
}
private boolean jude(ArrayList<Integer> list) {
for(int i = 0; i < list.size() -1; i++) {
if(list.get(i)> list.get(i+1)) {
return false;
}
}
return true;
}
}
九、判断是否为完全二叉树
OJ链接
📌📌📌题目描述:

返回值: boolean
📌📌📌解题思路:
利用完全二叉树的性质, 如果中间下标位置的结点有空缺, 说明不是完全二叉树
所以对这棵树进行层序遍历, 利用队列这种数据结构, 根节点入队, 当队列不为空时进入循环, 出队一次, 并让它的左右孩子结点入队(队列可以offer(null), 优先级队列不可以), 出队时遇见 null, 退出循环
退出循环后检查队列中剩余数据是否还有非空数据, 如果存在非空数据说明不是完全二叉树
⚠️⚠️⚠️注意:
队列可以 offer(null), 优先级队列不可以
代码实现:
public class IsCompleteTree {
public boolean isCompleteTree (TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean mark = true;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (node == null) {
mark = false;
} else {
if (mark == false) {
return false;
}
queue.offer(node.left);
queue.offer(node.right);
}
}
return true;
}
}
十、判断是否为平衡二叉树
OJ链接
📌📌📌题目描述:
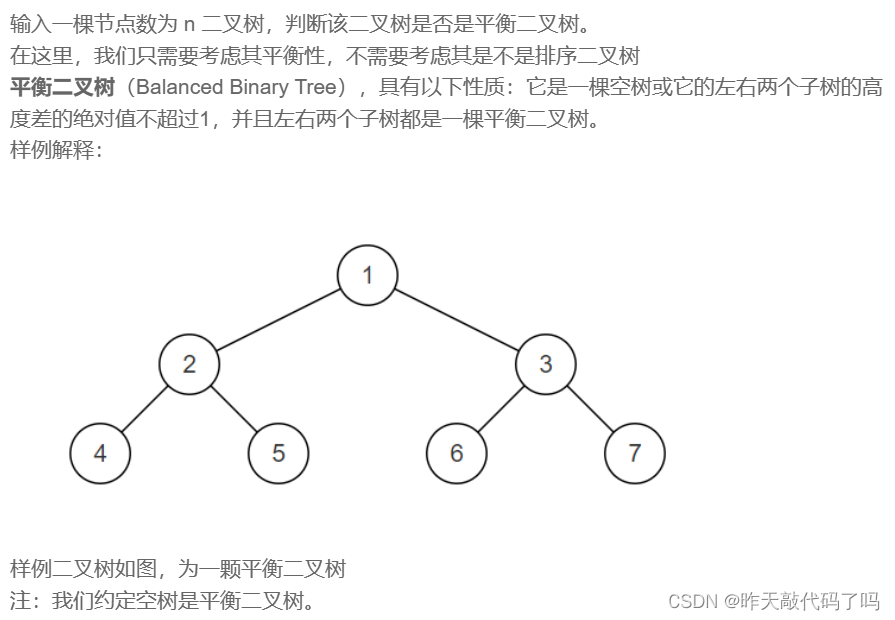
返回值: boolean
📌📌📌解题思路:
判断是否为平衡二叉树的规则就是左右子树高度差是否超过1, 典型的子问题思路
在判断树的高度代码上稍加修改即可
利用递归, 自下而上判断当前根结点所在的子树是否平衡: 获取了左右子树的高度之后, 相减取绝对值, 大于1说明不平衡, (所以要递归接收左右子树的高度)
⚠️⚠️⚠️注意:
如果发现子树不平衡, 那么整棵树一定不平衡, 所以当子树不平衡时就可以返回 -1, 减少对另一颗子树的无效递归, 一路返回-1, 最终在根节点判断时, 任何数和-1相减后去绝对值都大于1, 结论同样是不平衡
代码实现:
public class IsBalanced {
public boolean IsBalanced_Solution(TreeNode root) {
return treeHigh(root) >=0;
}
public int treeHigh(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null ) {
return 1;
}
int leftHigh = treeHigh(root.left);
if (leftHigh == -1) {
return -1;
}
int rightHigh = treeHigh(root.right);
if (rightHigh == -1) {
return -1;
}
if (Math.abs(leftHigh - rightHigh) <= 1) {
return Math.max(leftHigh, rightHigh) + 1;
} else {
return -1;
}
}
}
总结
以上是收录的十道关于二叉树的OJ题练习, 用作学习之余的整理分享, 仅供参考
如果本篇对你有帮助,请点赞收藏支持一下,小手一抖就是对作者莫大的鼓励啦😋😋😋~
上山总比下山辛苦
下篇文章见