刷题小抄1-2数之和

news2024/9/28 3:29:50

时间复杂度和空间复杂度

对于一个算法高效性的评估,分为时间复杂度与空间复杂度两种,在算法优化到极致的情况下,只能舍弃时间来换取空间,或者舍弃空间来换取时间,故而两者可以说是互斥关系

时间复杂度衡量的是算法运行的速度,而空间复杂度衡量的是算法运行所需要的额外内存空间

在计算机发展初期,计算机的存储容量很小,因此很在乎内存的消耗,也就是更看重空间复杂度,而如今时间复杂度才是决定算法优劣的主要因素

时间复杂度举例

如果存在循环,一般会对循环内使用时间最长(也是运行次数最多的语句进行时间复杂度的估算),例如以下代码中表示n*n矩阵相乘

我们找到最里面的嵌套了三层的循环语句,它被执行了n*n*n次,由于在n很大的时候(时间复杂度计算通常都默认考虑n为大数),执行该句的次数要远远大于其他语句,所以其他语句的执行时间我们都可以忽略,该算法的时间复杂度记为O(n^3)

其他常见的时间复杂度举例:

常数阶O(1):一般发生在没有循环的简单代码中

线性阶O(n):一般发生在一层循环的代码中

平方阶O(n^2): 一般发生在双层循环中

对数阶O(logn):一般发生在二分算法中

ps:

注意并不是有k层循环,时间复杂度就是O(n^k),主要还是得分析运行次数最多的语句和n之间的关系

空间复杂度举例

空间复杂度比较简单,假如对于一个有n个数的数组,你的算法使用常数个变量就能解决问题,那么你的空间复杂度为常数阶O(1),假如你需要额外使用一个同样长度为n的数组或容器来解决该问题,那么你的空间复杂度就为O(n)

两数之和

题目链接

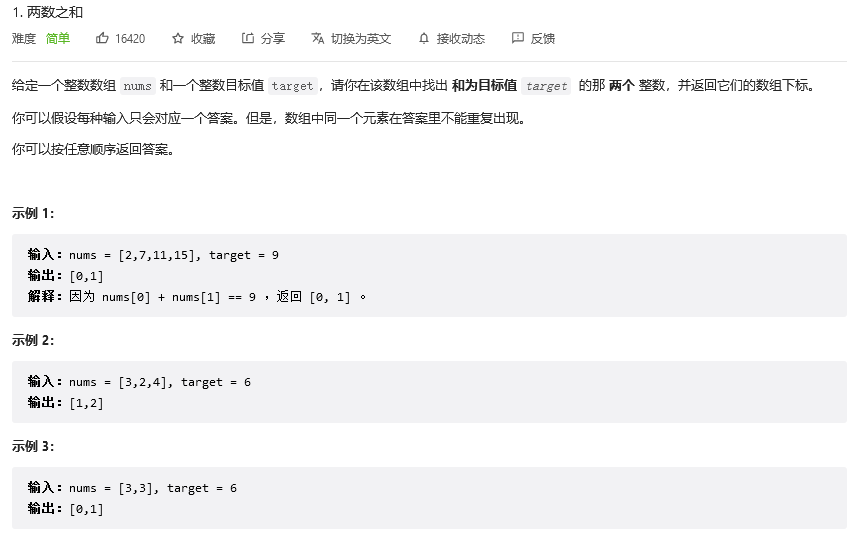
解法一: 双重循环遍历

这是最容易想到的一种解法,通过双重循环不停将两个数字组合,直到找到target,如果使用该解法我们只需要i,j两个指针辅助我们进行遍历,时间复杂度为常数故而为O(1)

对于最坏的情况下,我们在双重循环的末尾才能找到目标,也就是数组中任意两个数都要匹配一次,所以时间复杂度为O(N^2),其中N表示的是元素的数量

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    return [i, j]
        
        return []

对于数组为[1,2,3,4,5]寻找target为7,其i,j搜索的方式如下:

i=1时搜索j=2,3,4,5

i=2时搜索j=3,4,5

在i=2,j=5时找到答案,返回结果,否则返回一个空数组

解法二:使用哈希表存储记录过的值

解法一中时间复杂度较高是因为对于数组[1,2,3,4,5],程序对target-x这个值没有感知,其中x是当前遍历到的数组中的值

已知target为7,当我们在搜索[1,2,3,4,5]这个数组的时候,能不能通过一次遍历,不使用双重循环,在搜索到5的时候感知到我们曾经搜索过2(target-x)数字呢,这里就需要使用额外空间了,只要使用一个容器,记录曾经遍历过的数字,然后在这个容器中寻找是否有target-x即可

初学者可能会有疑问,既然还要在容器中把target-x再找到,那岂不是又要遍历一遍,时间复杂度还是没有下降,没错,正常容器不可以,但是哈希表可以,在python中它的名字是hashtable,进入它的元素,它都能使用O(1)时间复杂度给你查找出来,这是它的强大之处,它的存储形式为(key,value)键值对,加入向hashtable中插入(key,value1)与(key,value2)那么value2的值会覆盖掉value1的值,因此hashtable还有去重的作用

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
#初始化哈希表
        hashtable = dict()
        for i, num in enumerate(nums):
#如果查找到了target-x
            if target - num in hashtable:
#返回结果
                return [hashtable[target - num], i]
#该句中将(nums[i],i)这个数对放入hashtable中
            hashtable[nums[i]] = i
        return []

时间复杂度: O(N),我们只遍历了一遍所有的元素

空间复杂度: O(N),主要是我们使用了哈希表这个额外的容器