在许多情况下，回溯算法相当于穷举搜索的巧妙实现。回溯算法的一个具体例子是在新房子里摆放家具，开始什么也不摆放，然后每件家具被摆放在房间的某个位置，如果所有的家具都被摆放得令户主满意，那么算法终止；如果摆到某一步，该步之后的所有摆放方法都不能满意，那么就需要撤销这一步，并尝试其他的摆放方法，如果发现撤销了所有可能的第一步，就不存在令人满意的摆放方法。虽然回溯算法基本上是蛮力的，但它并不直接尝试所有的可能。例如，将沙发摆放进厨房的可能是不考虑的。在一步之内删除一大组可能性的做法叫作裁剪。

设给定个点，它们位于轴上。是点的坐标。进一步假设以及这些点从左到右给出。这个点确定在每一对点间的个(不必是唯一的)形如的距离。显然，如果给定点集，那么容易以时间构造距离的集合。这个集合将不是排序的，但是，如果我们愿意花时间界整理，那么这些距离也可以被排序。收费公路重建问题是从这些距离中重新构造一个点集。当然，若给定该问题的一个解，则可以通过对所有的点加上一个偏移量而构建无穷多其他的解。这就是为什么我们一定要将第一个点置于0处以及构建解的点集以非降顺序输出的原因。

令是距离的集合，并设，设

 首先，置，找到中的最大元素（最大的距离对应的点的位置只有两处，且点的位置只需要参考两个端点），显然，并从中删除距离10，

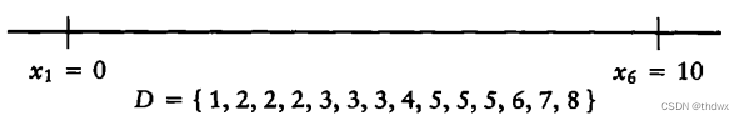
接下来找到中最大的元素8，由于和是对称的，所以或都是合理的，置，从中删除，得到

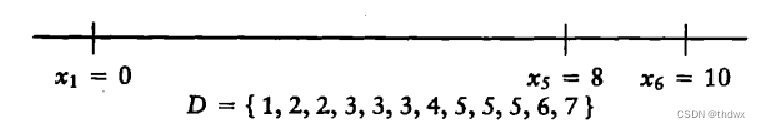
接下来选择距离7，此时有两个选择,发现这两个点与其余三个点的距离都属于，那么此时就任选一个点使算法先进行下去，如果后面会出现矛盾，则退回来尝试另一个选择。选择并删除对应距离，得到

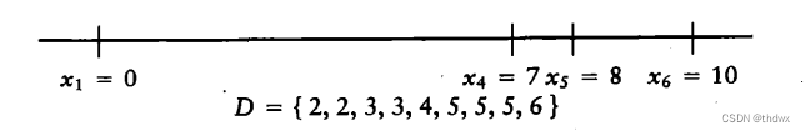
接下来选或，但由于不属于，且，而中只有一个4，所以这两个选择都是不符合要求的，那么就需要退回上一步尝试

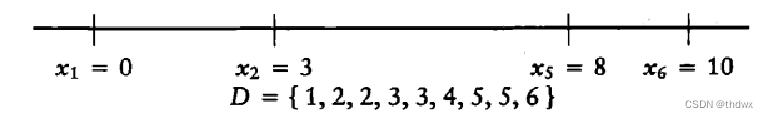
接下来选择或，易得只有符合条件，所以

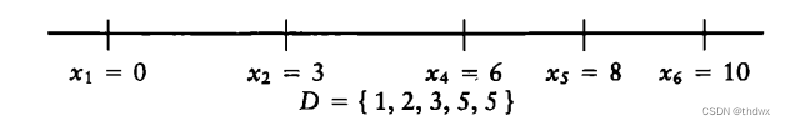
 最后一步只能有，且发现能删除中的所有距离并不会产生中没有的距离，所以此算法成功地重建了公路。

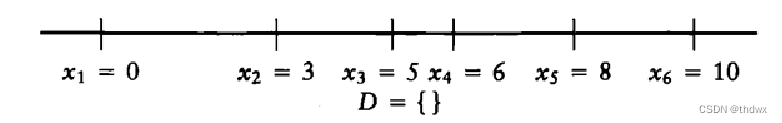
如图是一棵决策树，代表为得到解而采取的行动。这里没有对分支做标记，而是将标记放在了节点中。带有一个星号的节点表示这些所选的点与给定的距离不一致；带有两个星号的节点只有将不可能的节点作为儿子节点，因此表示一条不正确的路径。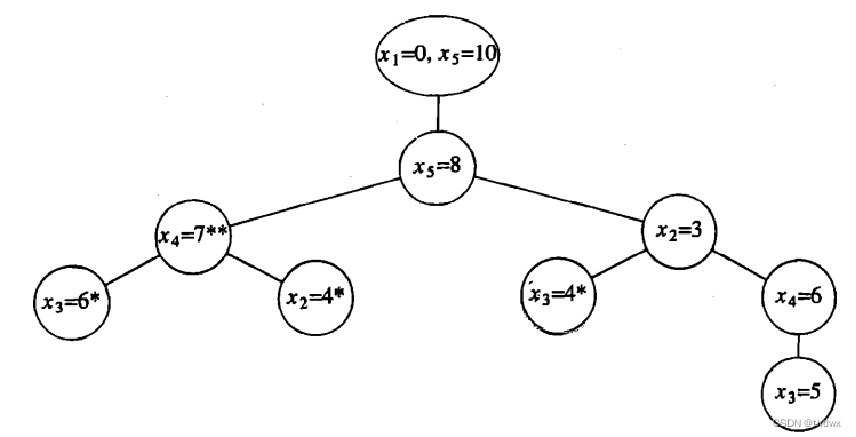

收费公路重建代码： 

#include<stdio.h>
#include<stdbool.h>
#include<math.h>

int deletemax(int dis[], int discopy[]) {//删除距离集合中的最大值
	int index, max = -1;
	for (int i = 0; i < 15; i++) {
		if (dis[i] > max) {
			max = dis[i];
			index = i;
		}
	}
	dis[index] = -1;
	discopy[index] = -1;
	return max;
}

int findmax(int dis[]) {//找到距离集合中的最大值
	int max = -1;
	for (int i = 0; i < 15; i++) {
		if (dis[i] > max)
			max = dis[i];
	}
	return max;
}

void copy(int dis1[], int dis2[]) {//将一个集合复制到另一个集合
	for (int i = 0; i < 15; i++) {
		dis1[i] = dis2[i];
	}
}

bool find(int x[], int dis[], int discopy[], int npot, int N) {//判断新增加的点与其余点的距离都在集合中，npot表示新增点的坐标
	for (int i = 1; i <= N; i++) {
		int d = 0;
		if ( x[i] != -1 && (d = abs(npot - x[i]))) {//如果当前位置有点并且不是新增点本身
			int j = 0;
			for (; j < 15; j++) {
				if (dis[j] == d) {//如果新增点与该点的距离存在于集合中，则在集合中删除该距离
					dis[j] = -1;
					break;
				}
			}
			if (j == 15) {//说明有距离不存在于集合中
				copy(dis, discopy);//通过副本将刚才删除的距离添加回集合
				return false;
			}
		}
	}
	copy(discopy, dis);//如果所有距离都存在，则更新副本
	return true;
}

bool isempty(int dis[]) {//判断集合是否为空
	for (int i = 0; i < 15; i++) {
		if (dis[i] != -1)
			return false;
	}
	return true;
}

void Insert(int x[], int dis[], int pos, int N) {//将删除的距离重新插入到集合中
	for (int i = 1; i <= N; i++) {//pos表示需要重新放置的点的现坐标
		if (x[i] != -1) {//当该位置有点时
			int d = abs(pos - x[i]);//将它们的距离算出来，重新放回集合
			for (int i = 0; i < 15; i++) {
				if (dis[i] == -1) {
					dis[i] = d;
					break;
				}
			}
		}
	}
}

bool place(int x[], int dis[], int discopy[], int N, int left, int right) {
	bool found = false;//将found设置为false
	if (isempty(dis))//如果集合为空，则说明算法已经成功
		return true;
	int max = findmax(dis);//找到集合中的最大距离，这时新增点只有两种摆放情况
	if (find(x, dis, discopy, max, N)) {//如果将其摆放在靠右的位置且其与其他点的距离都在集合中
		x[right] = max;//则先尝试靠右的可能
		found = place(x, dis, discopy, N, left, right - 1);//递归放置新点
		if (!found) {//如果后续摆放不能成功，则需要尝试另一种可能
			x[right] = -1;
			Insert(x, dis, max, N);//将这一步删除的距离重新加入集合中
			copy(discopy, dis);
		}
	}
	if(find(x, dis, discopy, x[N] - max, N)){//如果靠左的位置符合要求，则进行与上面相同的步骤
		x[left] = x[N] - max;
		found = place(x, dis, discopy, N, left + 1, right);
		if (!found) {
			x[left] = -1;
			Insert(x, dis, x[N] - max, N);
			copy(discopy, dis);
		}
	}
	return found;//返回结果
}

bool TurnPike(int x[], int dis[], int discopy[], int N) {//初始化公路
	x[1] = 0;
	x[N] = deletemax(dis, discopy);//第一个点和最后一个点显然是确定的
	x[N - 1] = findmax(dis);//而根据对称性，第三个点可以靠近左端点也可以靠近右端点，这个点也是确定的
	if (find(x, dis, discopy, x[N - 1], N)) {//如果新增的点与其余已经存在的点的距离都存在于集合中，则说明这个点的位置目前是合理的
		return place(x, dis, discopy, N, 2, N - 2);//通过递归放置其余点
	}
	else {//如果第三个点都无法摆放，说明这个集合的要求无法实现，返回false
		return false;
	}
}

int main() {
	int dis[15] = { 1,2,2,2,3,3,3,4,5,5,5,6,7,8,10 };//一组距离集合，重建的公路要满足这些条件
	int discopy[15] = { 1,2,2,2,3,3,3,4,5,5,5,6,7,8,10 };//距离集合的副本
	int x[7] = { -1,-1,-1,-1,-1,-1,-1 };//公路上的点
	if (TurnPike(x, dis, discopy, 6))
		printf("收费公路重建完成！\n");
	else
		printf("收费公路重建失败！\n");
	return 0;
}